Исследование и методика теоретического обоснования параметров технологических процессов формообразования монолитных панелей для конструкций летательных аппаратов

Кроме этого, нужно иметь теоретическое представление о характере влияния параметров техпроцесса на погрешности формы, свойства материала для определения требований к режимам исполнения операций, влияющих в наибольшей степени на отклонения от теоретически заданной формы профиля панели. Сложность моделирования процессов формообразования панелей принципиально обусловлена также и физической, геометрической и контактной нелинейностью процессов: В частности, исследование физической нелинейности как нелинейности определяющих соотношений свойств материала является необходимым условием моделирования процессов формообразования вследствие необходимости учета необратимых деформаций, которые могут быть описаны моделью упругопластического материала. Современные высокопрочные лёгкие сплавы требуют больших упреждающих перемещений при упругопластической деформации панелей, следовательно, без учета геометрической нелинейности в виде нелинейности уравнений равновесия и кинематических связей при описании изменения геометрии заготовки в процессе деформирования сложно провести объективное моделирование процессов формообразования для выбора усилий и степени деформации и условий разгрузки заготовки. Учет контактной нелинейности необходим при определении заранее неизвестной границы контакта заготовки и штамповой оснастки, а также сил, действующих в области их контакта.

В условиях автоматизации процессов формообразования панелей на базе оборудования с числовым программным управлением (ЧПУ) одним из эффективных способов формообразования геометрического контура монолитных панелей является гибка на прессах и прокатка на копировально- гибочных прессах без снижения усталостной прочности изделия после процесса прессования. Следовательно, гибку как технологическую операцию деформации панелей следует классифицировать по признакам приложения внешних нагрузок при гибке моментом, гибке поперечной силой, гибке с растяжением или сжатием, а также по признаку формы и размеров деформируемых заготовок, параметров силового набора и др.

Рис. 1. Схема напряженно-деформ ированного состояния панели при гибке

Исследуем изгиб моментом плоской панели с отношением длины к ширине более трёх, с текущими радиусами кривизны наружной и внутренней поверхностей соответственно R и r, радиусом кривизны нейтрального слоя ρ и средней линии R_c. В процессе деформации слои, для которых R>ρ> r на деформируемом участке панели, будут испытывать удлинение в тангенциальном направлении (ε_о>0), а слои, для которых R c >ρ>r, испытывают сжатие (ε о <0) (рис.1), то есть имеет место объемно-напряженное и плоско-деформированное состояние, для которого необходимо определить условия упруго-пластической деформации. Анализ показал, что для описания условий упругопластического деформирования панелей при гибке наиболее применима теория малых упругопластических деформаций.

Наиболее опасным местом при изгибе заго- товки является наружная поверхность заготовки и зоны радиусов перехода от ребер жесткости к полотну обшивки и в зонах разнотолщинности самого полотна обшивки, так как именно здесь зарождаются концентраторы напряжений, тре- щины и происходит разрушение заготовки при превышении предельных величин отношения rmin/S. Анализ напряженно-деформированного состояния (НДС) участков панели в угловых зонах показал, что там применима схема плоской деформации, материал можно сч итать изотр оп- ным и несжимаемым, а компоненты тензора напряжений зависят только от одной из координат. Другие допущения могут формироваться по мере постановки и решения соответствующих задач.

Анализ процессов деформации для построения методики обоснования конструкции проектируемой оснастки, расчёта условий устойчивости процессов деформирования показал, что при гибке угловых зон на первых переходах в открытых калибрах схема внешних воздействий близка к схем е гибки с растяжением, а на последних переходах, где осуществляется гибка заготовки по наружному контуру, схема внешних воздействий близка к схеме гибки с торцевым сжатием. В первом случае заготовка, как правило, получает утонение, а во втором – утолщение. Для вычисления смещения нейтрального слоя и последующего определения изменения толщины панели в угловой зоне деформации применим метод расчёта по напряжениям для определения напряжений и положения нейтрального слоя, где уравнение равновесия угловой зоны имеет вид: ∂-

—^- l '----- = 0,               (1)

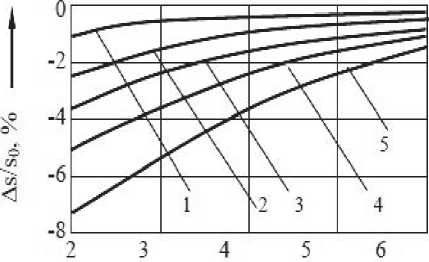
∂ где Ор,— -- радиальное и тангенциальное напряжение соответственно; ρ – текущее значение радиуса. Зависимость утонения (утолщения) металла от внутреннего радиуса и угла гибки при упругопластическом деформировании панелей при гибке показана на рис. 2 и 3.

Построенная модель дает весьма близкие результаты к экспериментальным данным по

Г. ММ ------"

Рис. 2. Зависимость утонения от внутреннего радиуса и угла гибки

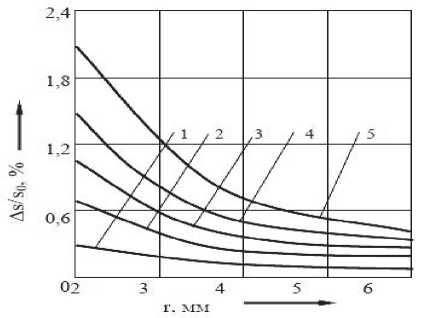
Рис. 3. Зависимость утолщ ения от внутреннего радиуса и угла гибки

ала в зоне пластического формообразования необходимо выполнить на основе аналитического описания соотнош ений между напряжениями и деформациями, точность вычисления которых определяет сложн ость теоретических расчётов параметров формообразования и погрешность получ аемых результатов. Для обеспечения практической применимости расчётной методики рассмотрим варианты аппроксимации кривой упрочнения материала панели (рис. 5).

утонению угловых зон на первых переходах, где среднее утонение составляет 3–4 %. Таким образ ом, исследуемая модель изменения толщины криволинейных участков заготовки в зависимости от расклада силовых факторов предполагает увеличение утонения или утолщения с уменьшением радиуса изгиба и с увеличением угла гибки. Анализ расчета параметров заготовки по разработанной модели показал достаточную точность результатов для разработки технологического оснащения, сокращ ения сроков и затрат на освоение технологии, повышения качества панелей и предотвращения потери устойчивости деформируемых элементов панели.

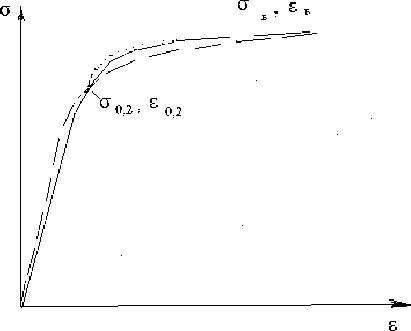
Рис. 5. Аппроксимация кривой упрочнения : сплошная линия – истинная кривая упрочнения; пунктирная линия – аппроксимация степенной функцией, точечная линия – линейно-степенной функцией

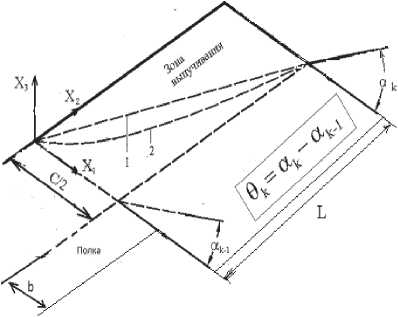
Рис. 4. Геометрические параметры панели в локальной системы координат:

1 – условная аппроксимация реальной границы пластической области;

2 – реальная граница пластической области

При степенной аппроксимации можно использовать для всего диапазона деформаций функцию вида:

ст = Ke" ,

где К – модуль упрочнения; n - показатель степенной аппроксим ации кривой упрочнения.

Вышеприведенная зависимость применяется в области пластических деформаций при использовании линейно-степенного закона. Аппроксимирующая функция в упругой области имеет вид: ст = Ее , где E -модуль упругости материала. Тогда пересечение графиков степенной и линейно-степенной функций происходит при относительной деформации: £_s = (—У/¹ ", где константы К и n ^E

В этом случае исходная формула для определения деформации панели имеет вид:

зависят от механических свойств материала и определяются из условия прохождения аппроксимирующей кривой через точки условного предела текучести и предела прочности истинной кривой упрочнения по соотношениям (рис. 5):

e

ev

eu

Следовательно, текущее значение деформа-

" = lg -^в- / £_s = lg -^в-

^ 0,2              *^£'о,2

в

K   ^в" , где ^0,2

ции можно вычислить по формуле:

e, = —т= ln i   Vs

1 + v

V

Sf( u )) ² ' d u J _j

Исследование механических свойств матери-

– условный предел текучести материала, определяемый по заданном у допуску на остаточную деформацию. Для аналитического описания схем изгиба широких заготовок, у которых ширина значительно больше толщины, можно принять схему плоского напряженно-деформ и-

рованное состояния, для которого следует применять приведенный модуль упрочнения К_пр :

7. , К — К (^)" пр лТз7

.

Практика теоретических расчётов остаточных величи н пластических деформаций и упруго го пружинения панелей с элементами комплексной формы сечения показывает, что эффективной может быть методика расч ёта технологических параметров упругопластической гибки, основанная на определении сначала положения нейтрального слоя в изгибаемом сечении, а затем вычисления кривизны изгибаемого элемента к = — по нейтральному слою, что позволяет Ra определить расстояние от нейтрального слоя до границы зоны упругой деформации. Тогда расчёт в зоне упругих деформаций производится по линейной зависимости = — еЕ, а в зоне пластической деформации по степенной зависимости с — КпрЕ". Сечение панели при этом разбивается на характерные участки с элементами комплексной формы сечения, строятся эпюры напряжений по отдел ьным участкам, а затем производится интегрирование эпюр напряжений по площади поперечного сечения в координатах ZY по схеме:

У н + h 2

yc

yн

^Ь1 ^Eka j ydy ^{+ Ь} 2 ^Eka j ydy ^{+ Ь} 2 ^K np^k J У " ^Ф У   =

yc

yн

У с                         ^h 1 ^- У н                         h 1 ^- У н ⁺ h 3

b,Ek. Jydy + b^" Jy"dy + ЬзK„к Jy'dy , 0                          Ус                             h 1 - Ун где Ь1, Ь2, b3 - ширина по горизонтальной оси Z характерных участков сечения; Е – модуль упругости материала; ka - кривизна по нейтральному слою; yí - расстояние от нейтрального слоя полок ребер жесткости элементо в комплексного сечения; Кпр– приведенный модуль упрочнения матер иала; kan – кривизна в зоне пластической деформации. Тогда методом последовательных приближений в зоне деформации можно вычислить положение нейтрального слоя yí , определяемое соотношением между кривизной нейтрального слоя и внеш ним изгибающим моментом:

M — kEJ уп + k " K пр J .л , (4)

где Jуп , Jпл – моменты инерции относительно нейтральной оси соответственно упруго й и пластически деформированной зон по высоте сечения, определяемые формой и кривизной деформируемого сечения. Описание состояния условного равновесия в зоне упругости может быть выполнено с использованием линейной зависимости между напряжениями и деформациями, где связь условной кривизны ki и изгибаю- щего мо мента Mz определяется соотношением: Mz — kEJ ,               (5)

где J – момент инерции суммарной площади поперечного сечения относительно нейтральной оси. Остат очная кривизна пластически изогнутого элемента k_o может быть определена из совместного реш ения уравнений (4) и (5):

k o = k . [ 1 - ( J ,. / J + K ., J . k ^{- 1}/ EJ ) ] .   (6)

Рассмотрим методику расчёта технологических параметров упругопластической гибки, связанную с применением шаговой процедуры интегрирования уравнений по параметру деформирования (времени) t для ф иксированной материальной точки. Требуется получить уравнения деформирования твердых тел, записанные в приращениях. Считаем шаг Δt достаточно малым. Предполагаем, что в момент t все искомые величины определены, то есть определяющее соотнош ение записывается в форме:

CT — С :£ , (7)

где C – тензор четвертого ранга, компоненты которого в общем случае зависят от компонент тензоров напряжений и деформаций (и, возможно, их скоростей); здесь и далее точка над величиной обозначает материальную производную, то есть частную производную этой величины по параметру деформирования (времени) t для фиксированно й материал ьной точки.

Тогда уравнение равновесия в слабой форме (уравнение принципа возможных перемещений или уравнение баланса виртуальных работ)

таково:

J а : 5sdV — J ff ■ UuVV + J T* • UuSs ,

v

v

S t

V Uu (5u — 0 c Su), (8) где ст и г являются соответственно симметричными тензорами напряжений и деформаций; u-вектор пер ем ещений; f-вектор объемных мас-совы х сил, действующих на единицу массы тела; V- занимаемая деформируемым телом область в базово й отсчётно й конф игурации; S-площадь замкнутой поверхности, ограничивающей область V; Su, ST - локальные области поверхности S (S — Su U ST , Su П ST — 0). На локальных поверхностях Su, ST заданы векторы перемещений u поверхностных сил Т = N ■ ст — ст ■ N : u — и на Su , где u*– текущее заданное значение u на Su , N ■ а — T * на SТ ; N–единичный вектор внешней нормали к поверхности ST ; р -удельная плотность деформируемого материала в базовой отсчётной конфигурации; точка в аналитических зависимостях между тензорами и векторами обозначает операцию их внутреннего произведения как свертки по одному индексу; знак (:) между тензорами обозначает операцию их внутренне- го двойного произведения как свёртки по двум индексам; знаком (δ) обозначена вариация переменной таким образом, что δu=0 на Su , то есть граничные условия на Su являются главными, а на ST - естественными.

Тогда кинематическое соотношение деформаций как связ ь тензора деформаций с тензором градиента перемещений имеет вид :

1                  T.

£ = ^(Vu + Vu ) ,

где ∇ u -тензор градиента перемещений, где ∇ - набла-вектор, который определяется по отношению к начальной базовой конфигурации объема деформируемой панели; верхний индекс (Т) обозначает операцию транспонирования.

Соответственно

⋅⋅

CT = С ".£ ,                   (9)

где C – тензор четвертого ранга, компоненты которого в общем случае зависят от компонент тензоров напряжений и деформаций (и, возможно, их скоростей); здесь и далее точка над величиной обоз начает материальную производную, то есть частную производную этой величины по параметру деформирования (времени) t для фиксированной м атериальной точки. В частности, к материалам, определяющие соотношения которых записываются в виде (9), относятся упругопластические материалы. Компоненты тензора

C для теории упругопластического течения, как для случая идеального, так и для материала с изотропным упрочнением, зависят от свойств деформируемых материалов.

Таким образом, используя аналогичную методику теоретических расчётов параметров деформации панели, можно получить линеар и-зованное уравнение равновесия в приращ ениях для расчёта параметров геометрической нелинейности в процессах деформ ирования панели, где в качестве отсчётной баз овой конф игурации принимается начальная конфигурация панели, а не текущая деформированная в некоторый момент времени процесса формообразования t, где V Su ( Su = 0 c S_u ) . Приведенная формулировка граничных усло вий при выборе определяющих соотношений упругопластического деформирования панелей с учётом относительно мал ых деформаций предпочтительна для по становки и решения задач формообразования панелей при геометрической нелинейности зависимостей параметров деф ормирования в условиях их пространственного напряженно-деформированного состояния. Исследование и анализ процессов деформации на базе программного комплекса DEORM -3D позволили получить значения текущих параметров деформации и напряжения по объему заготовки при заданных схемах деформации панелей, достаточно приближенные к расчётным.

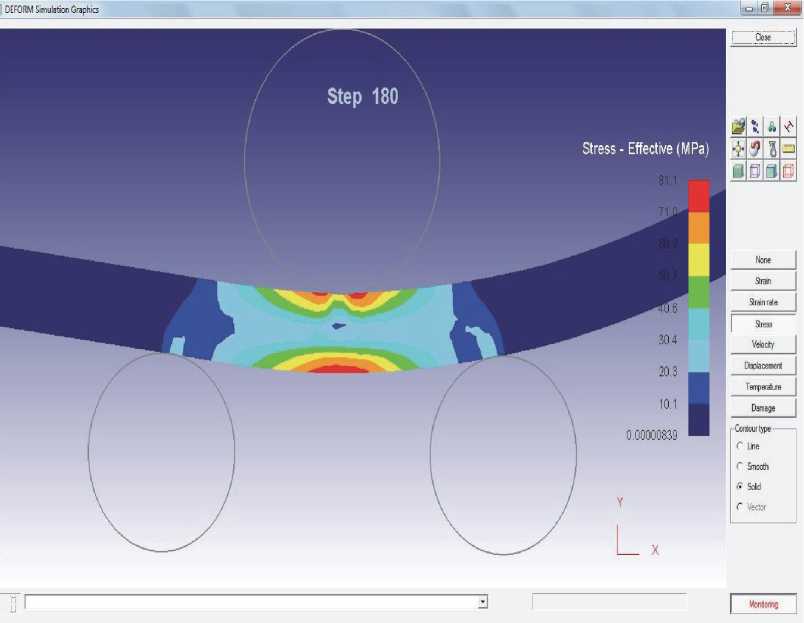
Рис. 6. Напряженно-деформированное состояние панели при формообразовании – гибке на опорах с регулируемым усилием на пуансоне на шаге 180