Исследование и оценка вибрационного состояния трубопроводных систем, деталей и узлов поршневых машин на основе аналитического моделирования

Интенсификация современных производственных процессов обусловила серьезное противоречие между постоянно увеличивающимися эксплуатационно-техническими и мощностными параметрами производственного оборудования, с одной стороны, и увеличением уровней возникающей при этом вибрации – с другой. Производственные вибрации опасны как с точки зрения воздействия на человека, так и влияния на надежность, эффективность и безаварийность работы машин и присоединенных систем, их деталей и узлов. Так, вибрация, превышающая допустимые значения, может явиться причиной разрушения соединений трубопроводов и аппаратов, нарушения герметичности уплотнений, и пр., что в условиях действующего производства может привести к самым серьезным последствиям.

Трубопроводные системы поршневых машин (компрессоров, поршневых двигателей и др.) имеют сложную пространственную конфигурацию, связанную с наличием коллекторных, байпасных магистралей, магистралей к пре-

дохранительным клапанам и т.д. Эти системы состоят из большого числа прямолинейных участков труб, между которыми расположены местные сопротивления - фасонные элементы, регулирующая и контрольно-измерительная аппаратура (вентили, задвижки, обратные клапаны, измерительные диафрагмы) и технологические аппараты (гасители колебаний, влагомаслоотде-лители, газоохладители). Поэтому расчет газодинамических колебательных процессов в трубопроводных системах поршневых машин и оценка вибрационного состояния деталей и узлов машин становится сложной задачей.

В данной статье рассматриваются возможности использования методов аналитического моделирования для упрощенного и вместе с тем позволяющего осуществлять достаточно точную оценку вибрационного состояния трубопроводных систем, деталей и узлов поршневых машин.

АНАЛИТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И РАСЧЕТ ВИБРАЦИИ ТРУБОПРОВОДНЫХ СИСТЕМ, ДЕТАЛЕЙ И УЗЛОВ ПОРШНЕВЫХ МАШИН

Линейный размер цилиндра поршневой машины и местных сопротивлений, как правило, намного меньше длины волны последней учитываемой гармоники колебаний, поэтому при расчетах их считают элементами с сосредоточенными параметрами. Традиционно расчет сводится к решению уравнений неустановивше-гося движения газа в прямой трубе постоянного сечения с граничными условиями, связанными с рабочим процессом в цилиндре компрессора, наличием местных сопротивлений и технологических аппаратов.

Поскольку длина прямолинейных участков труб значительно больше диаметра, а диаметр намного меньше длины волны последней учитываемой гармонической составляющей колебаний потока, то движение газа в трубопроводных системах поршневых машин можно считать одномерным. Одномерное неустановившееся движение газа цилиндрической трубе постоянного сечения описывается, как известно, системой уравнений газовой динамики, состоящей из уравнений неразрывности движения, энергии и состояния [4, 5]:

Проведем оценку амплитуд и частот колебаний газа в трубопроводной системе поршневой машины на примере поршневого низкооборотного компрессора. Время присоединения цилиндра поршневого компрессора к трубопроводу зависит от отношения давления в цилиндре ( £ ), но всегда меньше половины периода колебаний (время одного оборота вала для цилиндра простого действия). При £ = 4 время присоединения цилиндра к нагнетательному трубопроводу (продолжительность открытия клапана) не превышает 25% периода, а к всасывающему трубопроводу – 40% периода. Скорость газа в граничном с цилиндром сечении трубопровода без учета влияния работы клапанов и газовой полости меняется по закону:

to ( t ,0 ) =

F nR

K

sin to t + —— sin 2 to t

2 J to

V

где F_п - площадь поршня; S - площадь трубы;

R_k - радиус кривошипа;

to - круговая частота;

Л К - отношение длины шатуна к радиусу кривошипа;

t0 - момент открытия клапана;

tз - момент закрытия клапана.

t^{3 -} t o ^ t ^ t s -

При разложении в ряд Фурье этого импуль- са величины начальных гармонических составляющих колебаний и средней составляющей скорости оказываются одного порядка. В случае резонанса и резкого увеличения интенсивности колебаний амплитуда динамической составляющей скорости оказывается больше средней. Такие условия могут возникать и при сложении амплитуд нескольких гармоник. Поэтому в отдельные моменты времени на некоторых участках трубопроводной системы направление движения потока может меняться. Для того, чтобы диссипативные силы приводили к снижению амплитуд колебаний газа при изменении направления движения, диссипативный член должен быть записан в виде:

Л _т р 2 d

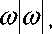
а перепад давления на местном сопротивлении -в виде

Pto

А Р = - . ~ И ,        (3)

где ^ _ст - коэффициент местного сопротивления.

В результате многочисленных измерений на промышленных и экспериментальных компрессорах установлено, что относительная амплитуда колебаний давления газа в трубопроводных системах

A_p = p- = 0,01 + 0,15

p p ₀                     .

Если, значительно занижая амплитуды колебаний скорости, использовать для определения параметров колебаний потока линейную модель p = р- c • to , то:

A . = "’ = /- = 0,01 +1,13 c kp ₀                 ^,

где K = 1,1 ^ 1,4 - показатель амплитуды, c - скорость звука.

При A _to >  0,01 амплитуды колебания газа считаются большими и на распространение волн существенное влияние оказывают нелинейные диссипативные и конвективные члены в уравнении движения. Если же A to ^ 0,01 , то амплитуды колебаний малы, и колебания можно считать акустическими.

Большие амплитуды колебаний скорости и давления газа приводят к тому, что колебания температуры сравнимы со средней составляющей. Поэтому теплообмен с окружающей средой может оказывать заметное влияние на амплитуды колебаний и при расчете колебательных газодинамических процессов в трубопроводных системах поршневых машин необходимо оценивать это влияние.

Для оценки частоты колебаний при наличии тепловых взаимодействий используется модифицированный критерий Био Bi , согласно которому в качестве характерного размера принято отношение скорости a _m распространения возмущения в металле к круговой частоте to .

Поскольку в трубопроводных системах поршневых компрессоров коэффициент теплопроводности материала труб Х _ш = 40ч70 Вт/мК, коэффициент теплопередачи a = 100ч200 Вт/мК, a _m = 5100 м²/с и to = 40 ^ 300 с - ¹, то:

Bi * = O^J^ = 0,2 ^ 0,6 ,    (6)

^Л ™ V ^to

Если Bi * = 0,01 , то колебания газа являются низкочастотными, а колебания температуры теплообменной поверхности и среды будут синхронными.

Таким образом, при расчете газодинамических колебательных процессов и выборе средств гашения колебаний в трубопроводных системах поршневых компрессоров необходимо учитывать, что относительные амплитуды возмущения скорости не малы, наличие средней составляющей приводит к турбулизации всего потока, газ не является идеальным, а теплообменом, особенно в газоохладителях, можно приводить к существенному изменению параметров колебаний.

Различный характер диссипативных процессов в электрических и газодинамических системах, наличие неоднородностей при разбиении участка трубы на элементы, и др., вносят в расчет существенные амплитудные погрешности, особенно для высших гармоник. Однако использование подобной модели позволяет значи-

тельно упростить процедуру расчета распределения амплитуд колебаний газа в сложных трубопроводных системах.

На основании электроакустической аналогии и теории подобия были разработаны критерии подобия, позволившие моделировать и рассчитывать газодинамические колебательные

U 1

AB

CD

U 2

^{- 1} 2

= [ A

U 2

^^^^^^^^

I 2

Элементы матрицы передачи [А] определяются выражениями:

A = chyL ; B = ZBshyl ;

С =   shyL ;D = chyL , (10)

ZB где Zв – волновое (характеристическое) сопротивление линии,

Y - постоянная распространения,

Z B

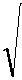
r + jtol' jtoc

Y = V( r + jtol)jtoc'.

Связь между входными параметрами четырёхполюсника может быть записана в вид уравнения:

U i a 2

i

= [ ^ ]? ;

_ i 2 _

;

i 1

i 2

= [y]

U 1

U г

процессы в трубопроводных системах поршневых машин, а также оценивать вибрационное состояние деталей и узлов машин.

Трубопровод поршневой машины моделируется в виде цепочечной схемы, параметры кото- рой определяются по линеаризованной системе уравнений [1, 5]. При моделировании гранич- ных условий потери на местных сопротивлениях линеаризировались по средней скорости.

При расчете временные зависимости преобразуются в частотную область через преобразо- вание Фурье:

to

Ф( )       pMto>jtotdto ,(7)

^{2 n} -»

где ф(to) — преобразование Фурье функции W),

ф(to) = J Ф( )e-j^dt ,(8)

-to

Если в уравнениях описывающих линейные процессы, ввести эти преобразования, то относительно функций Ф ( to ) получаются линейные алгебраические уравнения, которые достаточно удобно решать на ЭВМ.

Решение линейных уравнений для участка электрической линии конечной длины (см. рис. 1) зависит от граничных условий и может быть записано, например, в следующей форме:

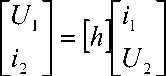
Элементы матриц a, z, y, h связаны между собой простыми соотношениями и легко могут быть преобразованы друг в друга.

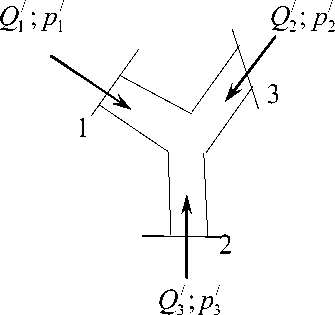
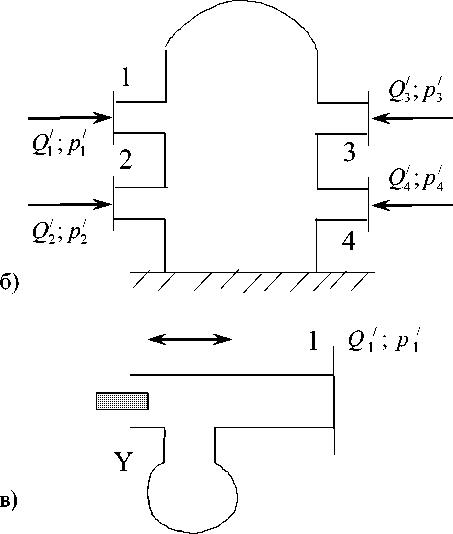
Кроме устройств с двумя граничными сечениями в компрессорных сетях необходимо рассматривать элементы и с большим, и с меньшими числом граничных сечений. Наиболее распространены устройства типа тройников, “четверников”, концевых сопротивлений, источников, и др., см. рис. 2. С точки зрения теории электрических цепей эти устройства могут рассматриваться как эквивалентные многополюсники: двух-, четырех-, шести-, и т.д. полюсни-

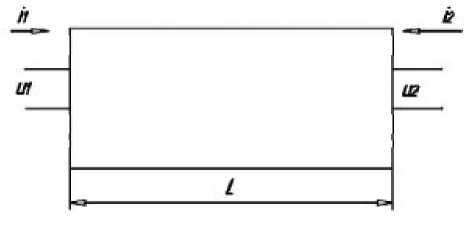
Рис. 1. Участок электрической линии конечной длины

а)

Q 1^/ ; p 1^/

--->

г)

Рис. 2. Принципиальные схемы элементов поршневой машины: а – тройник; б – четверник; в – источник; г – концевое сопротивление.

АППРОКСИМАЦИЯ ПРОЦЕССОВ ВСАСЫВАНИЯ И НАГНЕТАНИЯ

Процесс всасывания происходит во время движения поршня от верхней мертвой точки (в.м.т.) к нижней мертвой точке (н.м.т.). Сжатый в мертвом пространстве газ расширяется и давление его вначале достигает величины статического давления на впуске. Открытие впускного клапана происходит в момент, когда дополнительное разрежение в цилиндре достигает определенной величины, достаточной для создания открывающей силы. Заканчивается процесс всасывания при достижении поршнем н.м.т. Закон изменения объема цилиндра при движении поршня между верхней и нижней мертвыми точками приближенно может быть описан следующим образом:

V = V0 + V^ (1 - cos «1 • t) = V0 + Vh (1 - cosa), где «1 = 2n • f1 - круговая частота, _;

• f ₁ – частота вращения кривошипного вала компрессора, об/с;

a - угол поворота кривошипа, отсчитанный от в.м.т., рад.

После в.м.т. объем цилиндра уменьшается при закрытом впускном и выпускном клапанах. Газ в цилиндре сжимается. Будем условно считать, что выпускной клапан открывается в тот момент, когда давление в цилиндре компрессора достигает величины давления нагнетания. Этот момент соответствует следующей степени изменения объема:

• V . + V 0 = ^ i y

У.

ñæ

где V_сж - объём, соответствующий степени повышения давления в компрессоре е ;

Y - показатель политропы процесса сжатия.

Подставляя значение текущего объема по формуле (14) в выражение (15), получим для угла, соответствующего окончанию процесса сжатия, следующее выражение:

ки. Для источников эти многополюсники являются “активными”.

Путем совместного решения системы линейных уравнений, описывающих элементы компрессорной установки, можно вычислить, как это будет показано далее, колебания давления и объемных расходов во всех сечениях компрессорной установки, а также произвести необходимые оценки динамической ситуации.

где

cos а сж

1 - 2

1 + aM е1 ?

a M = V .             (17)

h

Учитывая далее, что угол а _сж лежит в пределах п <  а сж <  2 п , имеем:

О- = п + arccos сж

9 I ^{1 +} a M I ^ 1/ /

aM

- 1

Процесс сжатия происходит от н.м.т.

( a = п ) до угла а сж . Процесс выталкивания газа будем считать начинающимся мгновенно от угла а сж до в.м.т.

Аналогично угол открытия впускного клапана а вп определяется степенью расширения газа из мертвого пространства объемом V 0. При этом

V=^1

V о

или ам + 0,5(1 - cos авп) = ^1Y.  (20)

Далее имеем:

cos а вп = 1 - 2 a _M ( ^^Y - 1)    (21)

и авп = arccos[1 - 2aM (е^Y -1)]. (22)

ка два безмассовых поршня располагаются раздельно, а когда поток выходит из газовода, то они соединяются вместе. Допустим, что поршни, включающие плоский источник, размещены в позиции y , где y обозначает позицию координаты вдоль оси x (и не используется для координатной оси, ортогональной оси x ). Обозначим как U ( y + ) комплексную скорость в положительном направлении x с правой стороны поршня.

Комплексные колебания давления и скорости, возникающие в бесконечном канале, могут быть записаны как

■ p ( x ) = Р о • c 0 • U ( У + ) • e ■ x ^{- y 1} . u ( x ) = U ( y ₊ ) • e jk ⁽ x ^- y ⁾ ,

где x >  y .

Для области, где волны распространяются далее за источником, комплексные давления и скорости могут быть записаны как:

Р ⁽ x ) = Р о • ^c о • ^{U (} У - ) • ^{e -} jk ⁽ x ^- y ) u ( x ) = U ( y _ ) • e ^{- jk (} x ^{- y} ) ,

ОСОБЕННОСТИ АНАЛИТИЧЕСКОГО

МОДЕЛИРОВАНИЯ И ОЦЕНКИ ВИБРАЦИОННОГО СОСТОЯНИЯ ТРУБОПРОВОДНЫХ СИСТЕМ, ДЕТАЛЕЙ И УЗЛОВ ПОРШНЕВЫХ МАШИН

ПРИ НАЛИЧИИ АКТИВНОГО

КОМПЕНСИРУЮЩЕГО ИСТОЧНИКА

Рассмотрим активную компенсацию при одномерном распространении газового потока в газоводе поршневой машины, основанную на интерференции звуковых полей. При этом будем использовать плоский монопольный источник звука как основной элемент активной компенсации. Активная компенсация звука и вибрации в газоводах обычно осуществляется путём использования громкоговорителя или другого компенсирующего источника звука, и он, как правило, установлен на одной из стенок газовода.

Если мы ограничимся частотами меньшими, чем частота “среза” первой поперечной моды, то громкоговоритель в стенке канала будет генерировать плоские волны, распространяющиеся по каналу, и только в области, непосредственно близкой к громкоговорителю, будут генерироваться моды более высоких порядков. Эти моды образуют ближнее поле громкоговорителя.

Плоский источник представим в виде двух безмассовых поршней, разделённых бесконечно малым расстоянием. Эти поршни при поступлении колеблющегося объёма газа колеблются отдельно. При поступлении газовоздушного пото- где x > y ;

U ( y _ ) - комплексная скорость в положительном направлении x с левой стороны поршня.

Заметим, что положительная величина U ( y _ ) связана с отрицательной величиной давления, то есть движения поршня с левой стороны в положительном направлении генерируют идущие по направлению распространения разрежения.

Допустим далее, что плоский монопольный источник (первичный источник) полностью открыт для любого падающего звукового излучения; так как гипотетические поршни объединяют источник, не имеющий массы, они могут двигаться непосредственно с колебаниями скорости частиц, связанными с каким-либо другим распространением волны вдоль канала.

Будем считать, что объёмный поток, проходящий между двумя поршнями, не зависит от давления, производимого этими поршнями. Это означает, что громкоговоритель, моделируемый с помощью плосковолнового источника, имеет бесконечный внутренний акустический импеданс.

Упрощенную запись выражений для комплексного давления, генерируемого источником, можно получить при допущении, что x = y , так как давление постоянно вдоль источника. Тогда из уравнений (23) и (24) следует, что

Р ⁽ y ) = Р о • ^c о • ^{U (} у + ) = ^- Р о • ^c о • ^{U (} у - ) . ⁽²⁵⁾

Таким образом, можно получить, что U ( у ₊ ) = - U ( у _ ) , и если мы обозначим q ( у ) как объёмную скорость, вносимую в канал источником излучения, то мы можем записать следующее выражение:

и ( y + ) = - U ( y - ) = q ( y )/2 S ,     (26)

где S - площадь поперечного сечения в канале.

Общее давление может быть записано в форме:

- jk\x - y|

^{p (} x ) = q ⁽ y )^ S.   _<27)

Это выражение связывает комплексное давление, производимое в данном положении x , с объёмной скоростью источника q ( y ) в данном положении y . Так как величина колебаний давления явно связана с величиной колебаний объёмной скорости, то будем рассматривать величину q(y ) как комплексную силу источника плоской монополи.

Допустим, что первичный монопольный источник силой q_p помещён против направления распространения на расстояние x = 0 , а компенсирующий плоский монопольный источник силой q_s – против направления распространения на расстояние x = L , причём оба источника расположены в бесконечном канале. Комплексное давление, производимое двумя источниками, действующими независимо, может быть записано как

P p (' x ) = ^5qp ■ e (28)

P s ( x * = ^ M" q - ' e '- L .       (29)

Согласно принципам линейности и суперпозиции можно сложить колебания давлений первичного и вторичного источников и получить результирующее давление как их сумму. Иначе говоря, должно выполняться соотношение

P o • с 0

2 S

q p • e

- jkx

+ P o • с 0 2 S

q- • e

-jk\ x - L\

= 0, x >  L . (30)

Из этого выражения видно, что величина результирующего звукового давления будет определяться результатом сложения, или интерференцией, величин и фаз звуковых давлений первичного и вторичного источников при их распространении в заданном пространстве (в нашем случае в газоводе поршневой машины).

Из уравнения (30) следует, что можно подобрать такие амплитудно-частотные характеристики вторичного источника, что можно получить как эффект усиления, так и ослабления колебаний потока газа при интерференции.

ЗАКЛЮЧЕНИЕ

В работе показано, что расчет газодинамических колебательных процессов в трубопроводных системах поршневых машин и оценка вибрационного состояния деталей и узлов машин, осо-

бенно в области низких частот, могут быть достаточно эффективно осуществлены с использованием аналитических методов. Путем совместного решения системы линейных уравнений, описывающих элементы поршневой машины, можно вычислить колебания давления и объемных расходов во всех сечениях газовода поршневой машины, а также произвести необходимые оценки динамической ситуации.

Описан принцип аналитического моделирования основных элементов газоводных систем поршневых машин. Показана аппроксимация процессов всасывания и нагнетания, приведены принципиальные схемы элементов поршневой машины.

Описаны особенности аналитического моделирования и оценки вибрационного состояния трубопроводных систем, деталей и узлов поршневых машин при наличии активного компенсирующего источника.

С использованием разработанных аналитических и расчетных моделей произведены расчет колебательных процессов в системах газообмена поршневых машин и оценка вибрационного состояния трубопроводных систем, деталей и узлов поршневых машин различных типов [1, 2, 6, 7].

Работа выполнена при поддержке гранта по ведущим научным школам РФ 2008-2009 гг. (НШ-4245.2008.8) и в рамках программы “Развитие научного потенциала Высшей школы” Минобрнауки РФ