Исследование и определение оптимально-проходческой площади направляющего тоннеля при строительстве выработок большого поперечного сечения

В настояшее время на практике строительства и проходки тоннелей большого поперечного сечения обычно используют поэтапные схемы проходки для повышения скорости строительства и увеличения устойчивости пород массива вокруг выработки. Однако выбор соответствующей схемы для увеличения эффективности проходки и устойчивости выработки является сложной задачей. При поэтапной проходке определение площади каждого забоя тоже необходимо учитывать. Первое место проходки и также проходческая площадь в забое зависят от геологических условий и глубины положения выработки, а также от характеристик используемых средств. Данная статья представляет собой выбор оптимальной проходческой площади направляющего тоннеля в выработок большого сечения на основе численного метода по программе Phase 2. Рассматриваемая проблема также является основой для проектирования проходки и выбора конструкции крепи горной выработки.

Вводимые параметры породы массива для задачи можно увидеть в нижней части. В первом случае диаметр выработки 5, 10, 15, 20м, диаметр направляюшего тоннеля увеличивется, глубина заложения выработки 50м. Схема анализа рассматривается на рис 1 и 2.

Параметры массива породы для анализа:

Обьемный весс породы у = 0,026 MН/м³; прочность на растяжение СУ k = 0,01 MПa; сила сцепления c = 0.05 MПa; угол внутреннего трения = 35⁰; модуль упругости E = 1200 МПа; коэффициент Пуассона ц = 0,25; Угол расширения \|/ = 0⁰; угол избыточного внутреннего трения ф re = 36⁰; избыточное сцепление c re = 0,5 МПа; радиус выработки r 1 = 2,5; 5,0; 7,5; 10 м; радиус направляюшего тоннели - изменяется; коэффициент начальноого напряжения (горизонтальный/вертикальный) К = СУ 1 /СУ 3 = 0,5; глубина расположения горной выработки H = 50 м; тип материала -Пластичный; стандарт использования - Mohr - Coulomb; задача рассматривается плотность и начального напряжения в массиве.

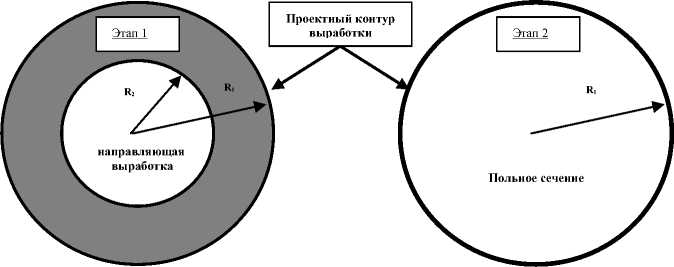
Рис 1. Теоретиеческая схема для задачи

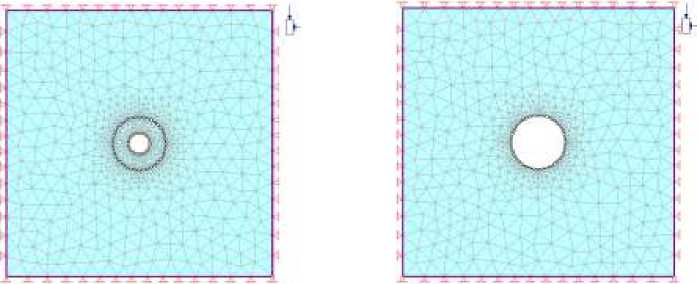
Этап 1                               Этап 2

Рис 2. Моделирование задачи по программе Phase 2

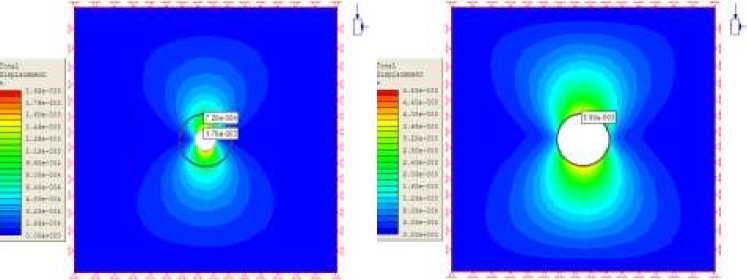
Рис 3. Результаты распределения суммарной деформации с поэтапной стадией при D1 = 5м и D2 = 1м

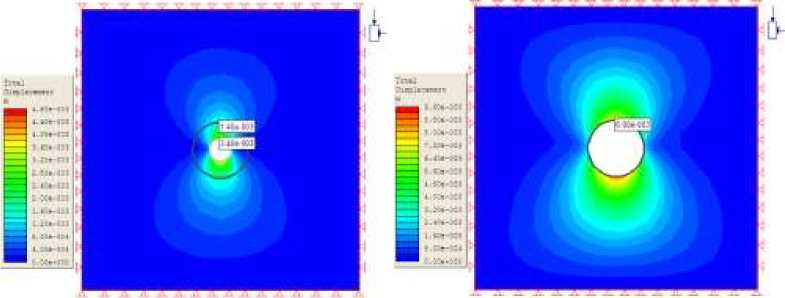
Рис 4. Результаты распределения суммарной деформации с поэтапной стадией при D 1 = 10м и D 2 = 4м

Таблица 1.

№	D 2 , м	Вертикальное напряжение в кровле, MПa	Горизонтальное напряжение в кровле, MПa	Суммарная деформация в кровле, м
1	1,0	0,71	0,04	0,00380
2	2,0	0,71	0,07	0,00380
3	3,0	0,71	0,04	0,00360
4	4,0	0,75	0,00	0,00340
5	5,0	0,71	0,04	0,00380

Напряженно-деформированные значения при D1 = 5м

Таблица 2.

Напряженно-деформированные значения при D1 = 10м

№	D 2 , м	Вертикальное напряжение в кровле, MПa	Горизонтальное напряжение в кровле, MПa	Суммарная деформация в кровле, м
1	2,0	0,64	0,04	0,00720
2	4,0	0,64	0,04	0,00680
3	6,0	0,64	0,04	0,00680
4	8,0	0,68	0,04	0,00665
5	10,0	0,64	0,04	0,00720

Таблица 3.

Напряженно-деформированные значения при D1 = 15м

№	D 2 , м	Вертикальное напряжение в кровле, MПa	Горизонтальное напряжение в кровле, MПa	Суммарная деформация в кровле, м
1	2,0	0,63	0,06	0,0102
2	4,0	0,62	0,06	0,0102
3	6,0	0,63	0,06	0,00960
4	8,0	0,67	0,06	0,00960
5	10,0	0,67	0,06	0,00960
6	12,0	0,67	0,05	0,00935
7	14,0	0,65	0,00	0,00960
8	15,0	0,63	0,05	0,0102

Таблица 4.

Напряженно-деформированные значения при D 1 = 20м

№	D 2 , м	Вертикальное напряжение в кровле, MПa	Горизонтальное напряжение в кровле, MПa	Суммарная деформация в кровле, м
1	4,0	0,57	0,05	0,0120
2	8,0	0,57	0,06	0,0113
3	12,0	0,62	0,06	0,0113
4	16,0	0,60	0,05	0,0113
5	18,0	0,52	0,00	0,0113
6	200	0,59	0,00	0,0120

Где: D 2 - диаметр направляющего тоннеля; D 1 - диаметр выработки

После анализа модели получаем разные напряжения и деформации и также график зависимости напряжения и деформации от диаметров направляющего тоннеля (табл. 1, 2, 3, 4 и на рис. 3, 4, 5, 6).

Связь между напряжением о 1 и диаметром D 2

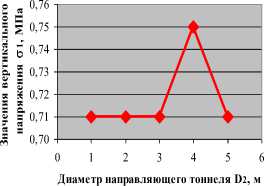
-•- напряжение на кровле выработки

Связь между напряжением 3 и диаметром D 2

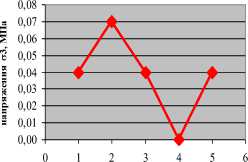
-♦- напряжение на кровле выработки

Диаметр направляющего тоннеля D 2 , м

• a)    Зависимость значения вертикального и горизонтального напряжения в кровле от диаметров направляющего тоннеля при D 1 = 5м

  
  
  

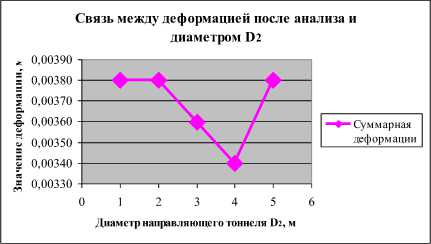
• б)    зависимость значения деформации от диаметров направляющего

тоннеля

Рис 3. График для определения оптимального диаметра направляющего тоннеля при диаметре выработки D 1 = 5м

Связь между напряжением 1 и диаметром D 2

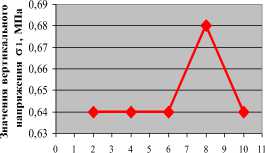
-♦- напряжение на кровле выработки

Диаметр направляющего тоннеля D 2 , м

Связь между напряжением 3 и диаметром D 2

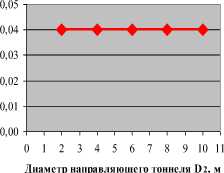
—•— напряжение на кровле выработки

• a)    Зависимость значения вертикального и горизонтального напряжения в кровле от диаметров направляющего тоннеля при D 1 = 10м

  Связь между деформацией после анализа и

  

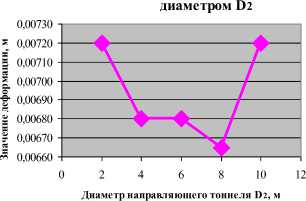
  —♦— Суммарная деформации

  
  

• б)    Зависимость значения деформации в кровле от диаметров направляющего тоннеля при D 1 = 10м

Рис 4. График для определения оптимального диаметра направляющего тоннели при диаметре выработки D 1 = 10м

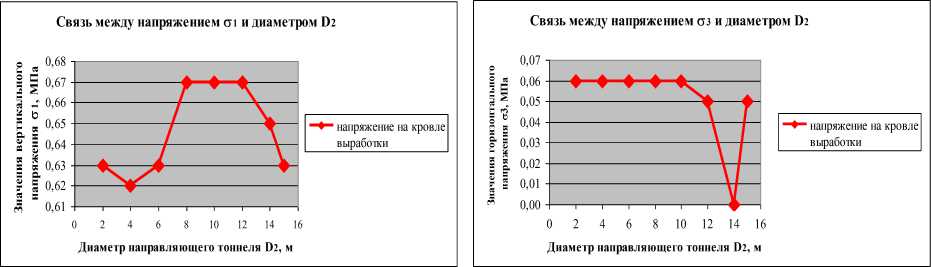
a) Зависимость вертикального и горизонтального напряжения в кровле выработки от изм енения диаметров направляющего тон неля при D 1 = 15м

Связь между деформацией после анализа и диаметром D 2

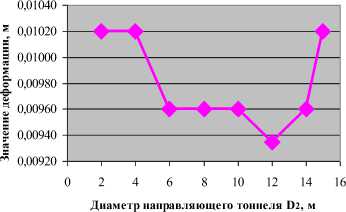
Суммарная деформации

• б)    Зависимость значения деформации в кровле выработки от диаметров направляющего тоннеля при D 1 = 15м

Рис 5. График для определения оптимального диаметра направляющего тоннели при диаметре выработки D 1 = 15м

Связь между напряжением о 1 и диаметром D 2

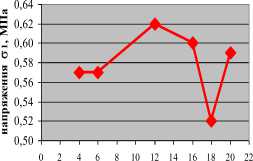
-♦- напряжение на кровле выработки

Диаметр направляющего тоннеля D 2 , м

Связь между напряжением 3 и диаметром D 2

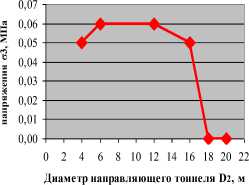
-*- напряжение на кровле выработки

• a)    Зависимость значения вертикального и горизонтального напряжения от

диаметров направляющего тоннеля при D 1 = 20м

Связь между деформацией после анализа и диаметром D 2

0,01210

0,01200

0,01190

0,01180

0,01170

i 0,01160

0,01150

0,01140

0,01130

0,01120

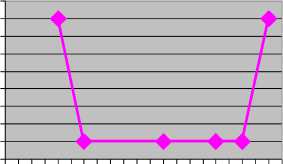
-♦- Суммарная деформации

0 1 2 3 4 5 6 7 8 9 101112131415161718192021

Диаметр направляющего тоннеля D 2 , м

• б)    Зависимость значения деформации от диаметров направляющего тоннеля при D 1 = 20м

Рис 6. График для определения оптимального диаметра направляющего тоннели при диаметре выработки D 1 = 20м

После анализа можем сделать выводы, что проходка направляющего тоннеля влияет на напряженно-деформированное состояние контура выработки меньше чем при проходке польного забоя. В зависимости от диаметров направляющего тоннеля значения напряжения и деформаций изменяются, в большинстве случаев при коэффициенте диаметра направляющего тоннеля и диаметра выработки равны 0,8 (D 2 /D 1 = 0,8). После анализа мы можем получить оптимальные следующие результаты:

При D 1 = 5м то D 2 = 4м (D 2 /D 1 = 0,8)

При D 1 = 10м то D 2 = 8м (D 2 /D 1 = 0,8)

При D 1 = 15м то D 2 = 12м (D 2 /D 1 = 0,8)

При D 1 = 20м то D 2 = 8м (D 2 /D 1 = 0,4)

Где D1 - диаметр выработки, м

D2 - диаметр направляющего тоннеля, м

Можно сказать, что этот результат является очень важным при использовании на практике направляющего тоннеля проходки вырботки со щитом (ТВМ - Tunnel Boring Machines).

Выводы и рекомендации

• -    Проходка направляюшего тоннеля влияет на напряженно-деформированное состояние вокруг выработки меньше, чем при проходке профильного сечения.

• -    При выработке направляющего тоннеля круглого сечения оптимальная площадь направляющего тоннеля соответствует следующим параметрам: при D 1 = 10, 15м коэффициент D 2 /D 1 = 0,8 (рис 3,4,5); при D 1 = 20м то D 2 /D 1 = 0,4 (рис 6).

• -    При диаметре выработки равном D₁ = 5м лучщий вариант диаметра направляюшего тоннеля равено D 2 = 4м (D 2 /D 1 = 0,8).

Эти выводы являют очень важными при строительстве выработки большого поперечного сечения. Мы можем определить точно площадь расположения направляющего тоннеля, повышать скорость проходки выработок и также устойчивость пород вокруг выработки и эффективность геологоразведки на практике.