Исследование и разработка алгоритмов анализа неструктурированной и слабоструктурированной информации

Неэффективное управление информацией ведёт к увеличению рисков для различных форм бизнеса: хранение персональных данных и прочей конфиденциальной информации на общедоступных информационных ресурсах, появление подозрительных пользовательских зашифрованных архивов, нарушения политик доступа к важной информации и т.д.

В этих обстоятельствах умение качественно анализировать информацию и оперативно реагировать на любые несоответствия её хранения политикам и требованиям бизнеса является ключевым показателем зрелости информационной стратегии организации.

Слабоструктурированная информация (ССИ) — это данные, для которых определены некоторые правила и форматы, но в самом общем виде. Например, строка с адресом, строка в прайс-листе, ФИО и т. п. В отличие от неструктурированных, такие данные с меньшими усилиями преобразуются к структурированной форме, однако без процедуры преобразования они тоже непригодны для анализа.

К неструктурированной информации (НИ) относятся данные, произвольные по форме, включающие тексты и графику, мультимедиа (видео, речь, аудио). Эта форма представления данных широко используется, например, в Интернете, а сами данные предоставляются пользователю в виде отклика поисковыми системами.

Проведем сравнение алгоритмов анализа неструктурированной и слабоструктурированной информации. К таким алгоритмам относятся следующие:

• -    алгоритмы поиска ассоциативных правил;

• -    алгоритмы кластеризации (методом агломерации, деления);

• -    алгоритмы задач классификации и регрессии (в т.ч. прогнозирование временных рядов);

• -    алгоритмы построения нейросетей и генетические алгоритмы.

В качестве критериев для сравнительного анализа выберем следующие:

1)A₁ – точность разбиения на группы;

2)A 2 – точность прогноза;

3)A₃ – точность нахождения закономерностей;

4)A 4 – анализ плохоформализуемых данных;

5)A 5 – нахождение скрытых закономерностей данных.

Для определения весов критериев воспользуемся аналитической иерархической процедурой Саати[4]. Правила заполнения матрицы парных сравнений представлены в таблице 1 .

Таблица 1. Значения коэффициентов матрицы парных сравнений

X ij	Значение
1	i -ый и j -ый критерий примерно равноценны
3	i -ый критерий немного предпочтительнее j -го
5	i -ый критерий предпочтительнее j -го
7	i -ый критерий значительно предпочтительнее j -го
9	i -ый критерий явно предпочтительнее j -го

Матрица парных сравнений, средние геометрические и веса критериев представлены в таблице 2.

Таблица 2. Матрица парных сравнений, средние геометрические и веса критериев

	А1	A2	A3	A4	A5	Среднее геометрическое	Веса критериев
A1	1	1/3	3	7	5	0,93	0,14
A2	3	1	5	9	7	3,94	0,40
A3	1/3	1/5	1	5	7	1,18	0,18
A4	1/7	1/9	1/5	1	5	0,44	0,06
A5	1/5	1/7	1/7	1/5	1	0,24	0,04
Сумма						6,73	1,00

Диаграмма весовых коэффициентов для критериев A₁ , A₂ , A₃ , A₄ , A₅

представлена на рис. 1.

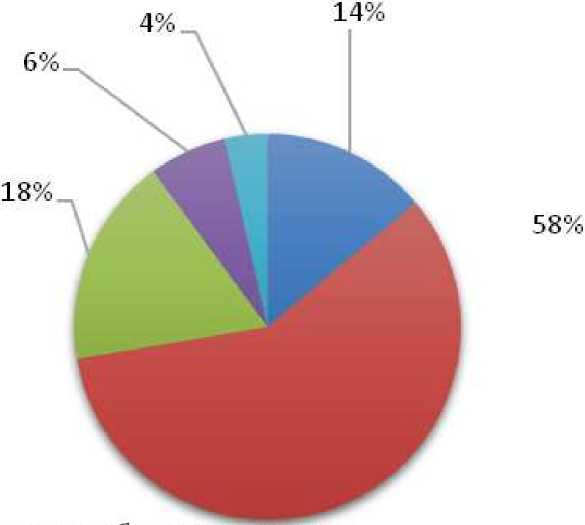
■ А1-Точность разбиения на группы;

• ■    А2-Точность прогноза;

• -    АЗ-Точность нахождения закономерностей;

• ■    А4-Анализплохоформализуемых данных;

• ■    А5-Нахождение скрытых закономерностей данных.

Рис. 1. Весовые коэффициенты критериев качества

Проведем проверку матрицы попарных сравнений на непротиворечивость[2, 5].

Суммы столбцов матрицы парных сравнений:

R 1 =4,68; R 2 =1,79; R 3 =9,34; R 4 =15,34; R 5 =25.

Путем суммирования произведений сумм столбцов матрицы на весовые коэффициенты альтернатив рассчитывается вспомогательная величина L = 5,23. Индексом согласованности (CI – Consistency Index)

CI =

L-N

N-1

= 0.2

Величина случайной согласованности (RI – Random Index) для размерности матрицы парных сравнений: RI = 1.12.

Отношение согласованности (CR – Consistency Ratio)

CI

CR =   = 0.18

0.18 не превышает 0.2, поэтому уточнение матрицы парных сравнений не требуется[3].

Используя полученные коэффициенты определим интегральный показатель качества для алгоритмов:

• 1.    Алгоритмы поиска ассоциативных правил.

• 2.    Алгоритмы кластеризации (методом агломерации, деления).

• 3.    Алгоритмы задач классификации и регрессии (в т.ч. прогнозирование временных рядов).

• 4.    Алгоритмы построения нейросетей и генетические алгоритмы.

Выберем категориальную шкалу от 0 до 7 (где 0 – качество не удовлетворительно, 7 – предельно достижимый уровень качества на современном этапе) для функциональных возможностей программных продуктов.

Значения       весовых       коэффициентов ai соответствующие функциональным возможностям продуктов:

• 1.    анализ слабоструктурированной информации: a₂ = 0.4;

• 2.    анализ неструктурированной информации: a 1 = 0.36;

• 3.    классификация документов по представленным категориям: a₃ = 0.15;

• 4.    генерация тематической структуры исследуемого текста: a₄ = 0.06;

• 5.    извлечение информации по конкретным объектам: a 5 = 0.03.

Определим (по введенной шкале) количественные значения функциональных возможностей X_i j ( таблица 3 ). Вычислим интегральный показатель качества для каждого программного продукта[3].

Таблица 3. Интегральные показатели качества

Критерии Веса Алгорит мы поиска ассоциат ивных правил Алгоритм ы кластериз ации Алгоритмы задач классификации и регрессии Алгоритмы построения нейросетей и генетические алгоритмы Базовые значения Точность разбиения на группы 0,14 6 6 4 6 4,4 Точность прогноза 0,58 0 0 0 0 0 Точность нахождения закономернос тей 0,18 3 3 5 7 3,6 Анализ плохоформал изуемых данных 0,06 0 0 0 7 1,4 Нахождение скрытых закономернос тей данных 0,04 5 3 7 7 4,4 Интегральный показатель качества Q 1,54 1,47 1,69 2,77 1,49 где Qj=∑ai*Xij интегральный показатель качества для j-го программного средства[4].

Построим лепестковую диаграмму интегрального показателя качества каждого программного продукта (рис. 2).

Алгоритмы поиска

Алгоритмы построения нейросетей и генетические алгоритмы

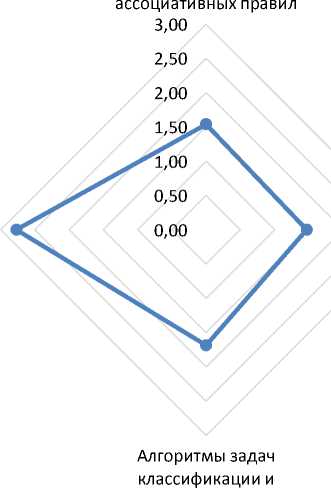
регрессии

Рис. 2. Лепестковая диаграмма интегральных показателей качества

Алгоритмы кластеризации

алгоритмов

Лепестковая диаграмма значений характеристик качества функциональных возможностей (критериев) представлена на рисунке 3.

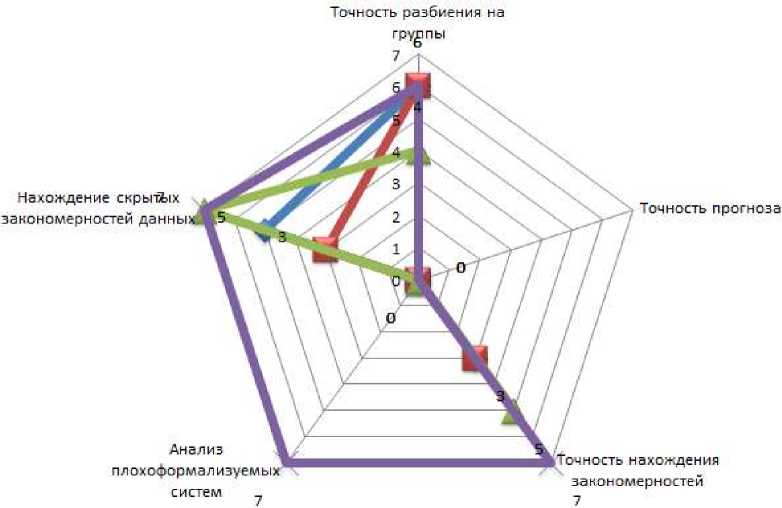
■^■Алгоритмы поиска ассоциативных правил

^^■Алгоритмы кластеризации

■ * -Алгоритмы задач классификации и регрессии

■^Алгоритмы построения нейросетей и генетические алгоритмы

Рис. 3. Лепестковая диаграмма значений функциональных характеристик

Сравнительный анализ алгоритмов анализа неструктурированной и слабоструктурированной информации показал, что три из четырех рассмотренных алгоритмов имеют значения интегрального показателя качества, превышающего базовое значение, - алгоритмы поиска ассоциативных правил, алгоритмы кластеризации, алгоритмы построения нейросетей и генетические алгоритмы. Из расчетов и графика интегральных показателей качества программных продуктов видно, что наибольший интегральный показатель качества имеет группа алгоритмов построения нейросетей и генетических алгоритмов.