Исследование и разработка на основе математического моделирования антирезонансных трансформаторов напряжения 220 кВ с разомкнутыми магнитопроводами

Меры по борьбе c феррорезонансными явлениями изложены в руководстве по защите электрических сетей 6-1150 кВ от грозовых и внутренних перенапряжений (РД 153-34.335.125-99), где в качестве одной из основных мер по борьбе с феррорезонансными явлениями предлагается использование антирезонанс-ных ТН. В настоящее время наиболее распространены антирезонансные ТН типа НАМИ, выпускаемые на ОАО «Раменский электротехнический завод «Энергия». Конструкция ТН типа НАМИ аналогична традиционным ТН типа НКФ, но в магнитопроводе помимо электротехнической применена также и толстолистовая конструкционная сталь. Потери энергии в стали снижают добротность колебательного контура, понижая тем самым амплитуду феррорезонансных колебаний. Как показали теоретические и экспериментальные исследования ТН НАМИ 500 кВ риск возникновения колебаний возможен на субгармонике 1/3. Кроме того, возможен резонанс при параллельной работе нескольких ТН на шинах подстанции, при этом антирезонансные свойства их снижаются [1-2]. В настоящее время на Раменском заводе ведётся работа по созданию антирезонансных ТН новой конструкции с разомкнутыми магнитопроводами [3, 4].

Обеспечение высоковольтной изоляции осуществляется секционированием, причем каждая секция – ферромагнитный стержень с обмотками. Один из разрабатываемых вариантов конструкции трансформатора легко размещается внутри фарфорового изолятора стандартного трансформатора тока (рис. 1), этому способствует отсутствие замкнутого магнитопровода. Катушки трансформатора могут иметь как вертикальное, так и горизонтальное расположение.

Рис. 1. Трансформатор напряжения

Расчет конструкции и режимов работы данного типа трансформатора не может быть выполнен стандартными методами, применяемыми для трансформаторов с замкнутыми магнитопроводами. Магнитное поле трансформаторов со стержневым магнитопроводом имеет разветвленное поле рассеяния, а основной магнитный поток только часть своего пути проходит по сердечнику. Использование существующих инженерных методик расчета трансформаторов, основанных на предположении того, что весь магнитный поток проходит и замыкается по ферромагнитному сердечнику, приводит к существенным погрешностям в результатах расчетов. Получение достоверных значений возможно только на основе расчёта электромагнитного поля трансформатора. В настоящее время для расчётов полей получили широкое применение компьютерные программы на основе метода конечных элементов, такие как ANSYS, ELCUT, COMSOL Multiphysics. Для расчета

ТН была выбрана программа COMSOL Multiphysics имеющая широкие возможности в области моделирования не только электромагнитных, но и тепловых, механических и др., а также имеющая возможности интеграции с пакетом Matlab.

Выполнение расчётов преследует следующие цели:

• •    определение статических (метрологических) параметров трансформатора, включающее анализ магнитного поля и на его основе определение собственных и взаимных индуктивностей обмоток;

• •    исследование динамических процессов трансформатора при взаимодействии с внешними элементами схемы с ёмкостными элементами выключателей;

• •    исследование распределения электрического поля трансформатора.

В качестве исходных данных для построения компьютерной полевой модели необходимы геометрические данные трансформатора или готовые модели, полученные, в том числе, с помощью программных средств, таких как AutoCAD или КОМПАС. Также при моделировании необходимо задавать электрические свойства материалов (электропроводность и магнитную проницаемость).

Отдельные секций трансформатора – ферромагнитные стержени с обмотками – обладают осевой симметрией (рис. 2), поэтому для выполнения расчётов можно использовать двухмерное (2D) моделирование. При симметричном вертикальном расположении катушек в режиме 2D можно моделировать весь трансформатор, при горизонтальном расположении катушек необходимо использовать режим трёхмерного моделирования – 3D.

Рис. 2. Секция ТН, состоящая из ферромагнитного сердечника и обмоток

Важным этапом в создании модели является разбиение расчётной области на сеть конечных элементов, которая должна быть по возможности более мелкой, но при слишком мелкой сетке возникают погрешности из-за округления чисел в ЭВМ. Традиционно в качестве конечных элементов используются треугольные элементы, однако как показали вычислительные эксперименты, наибольшая точность расчётов получается при использовании сочетания прямоугольных и треугольных элементов. Разбиение расчётного пространства на конечные элементы в 2D и 3D моделях представлено на рис. 3 и рис 4 соответственно.

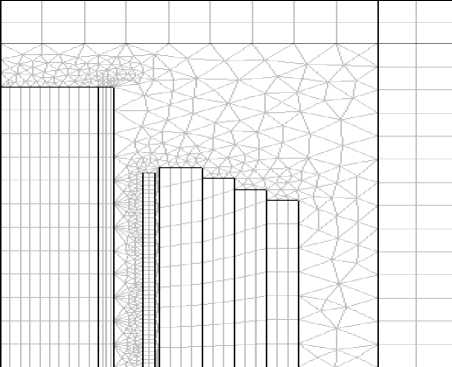
Рис. 3. Сеть конечных элементов в 2D модели

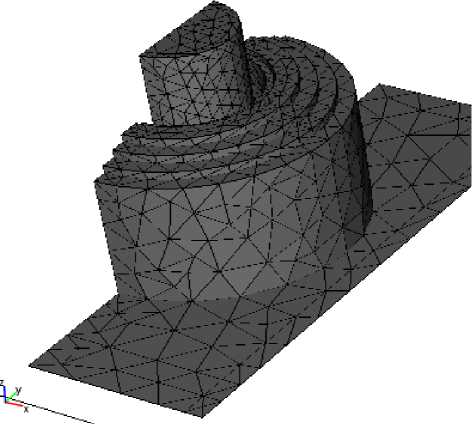
Рис. 4. Сеть конечных элементов в 3D модели

Определение метрологических параметров требует проведения расчётов с высокой точностью. Режимы работы трансформатора при определении погрешностей такие же, как и при реальных испытаниях, определяются при заданном напряжении и неизменной нагрузке (номинальной и ¼ от номинальной). Полевые расчёты направлены на определение собственных и взаимных индуктивностей, получаемых на основе решения статического или квазистатического полей с помощью, представленных ниже уравнений (1) и (2) соответственно. Уравнение, записанное в пространственной области, позволяет определять значения векторного магнитного потенциала во всех точках расчётной области:

V х ( д₀ 1 ц ¹ V х A ) = 7

где V - дифференциальный оператор Гамильтона, ц о =4я^10 7 Гн/м, ц - относительная магнитная проницаемость, A - векторный магнитный потенциал, J – вектор плотности сторонних токов. Недостатком использования данного уравнения является невозможность учёта наведённых вихревых токов в элементах конструкции трансформатора.

Уравнение в пространственно-частотной области имеет вид:

(jtoa A) + V х Ц 1ц 1V х A)= 7

,        (2)

где j = 7-1 , ю =2nf - угловая частота, о -электропроводность (проводника обмотки).

При соответствующем выборе координат и благодаря осевой симметрии катушек векторы плотности тока и векторного магнитного потенциала имеют только одну угловую компоненту: 7 = А _ф 1 ^ и A = А _ф \ _ф . Плотности токов в катушках задаются исходя из соотношения:

7 = I * n = S

,

где I – сила тока, протекающего в катушке, n – число витков катушки, S – площадь поперечного сечения катушки.

Следует отметить, что задаваемые плотности токов в моделях катушек будут меньше реальной плотности тока в проводах обмоток из-за наличия межслойной изоляции и неполного заполнения (коэффициента заполнения). Реальная плотность тока в проводниках обмоток j пр определяется по формуле:

j пр =I/S пр , (4)

где S пр - площадь поперечного сечения обмоток.

Расчёт трансформатора по уравнению (2) позволяет учесть не только токи в обмотках трансформатора, но и наведённые токи в металлических элементах конструкции трансформатора. При соблюдении определённых условий можно также учесть наличие вихревых токов в пластинах сердечника. Однако расчёт по уравнению (2) требует несколько больше компьютерных ресурсов по сравнению с решением по уравнению (1). При моделировании необходимо вводить граничные условия, учитывающие распределение магнитного поля на границах расчётной области.

Учёт вихревых токов в отдельных пластинах непосредственно только методом конечных элементов без приближений приводит к тому, что область сердечника разбивается на такое большое количество конечных элементов, что не только расчёты в 3D, но и в 2D (рис. 5) на современных ПК практически невозможны. Один из вариантов учета вихревых токов в пластинах сердечника предложен в [7] в виде задания эквивалентной проводимости сердечника (во много раз большей реальной проводимость стали), как бы учитывающей электрическую изоляцию между пластинами. Однако такой подход не учитывает различное значение индукции магнитного поля в различных частях сердечника и требует выполнения итераций, заключающихся в подборе эквивалентной проводимости сердечника с целью соответствия потерь в сердечнике и индукции магнитного поля. Другой подход заключается также в эквивалентной замене шихтованного сердечника сплошной средой, не обладающей электропроводностью (в расчётах всё же необходимо задавать электропроводность отличную от нуля, чтобы исключить возникновение сингулярности). При этом основное уравнение поля (2) дополняется соотношениями, позволяющими учесть возникающие потери от вихревых токов и снижение индукции в сердечнике, вызванное теми же вихревыми токами. Картины электромагнитного поля, полученные в результате расчёта, представлены на рис. 6 в виде силовых линий магнитного поля (линий равного магнитного потенциала).

Выполненные расчёты на моделях позволили более правильно распределить витки катушек по слоям, исходя из ЭДС электромагнитной индукции, приходящейся на один виток. Картина поля распределения ЭДС представлена на рис. 7. Наиболее выгодное место расположения витков находится в центральной части катушки, поэтому крайние витки можно перенести в центральную часть, увеличив радиальный размер катушки до максимально возможного размера (вплоть до стенок изолятора).

Рис. 5. Картина магнитного поля в 2D-модели

Рис. 6. Картина магнитного полей в 3D-модели

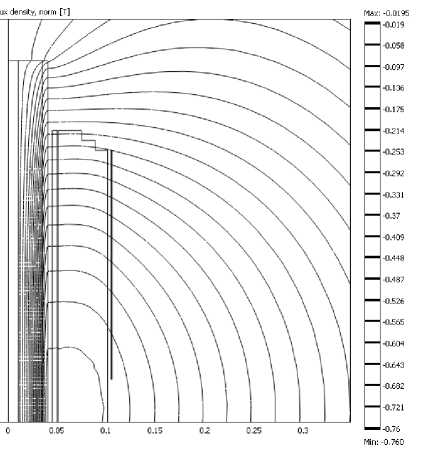
Рис. 7. Распределение ЕДС электромагнитной индукции на один виток катушки

По результатам расчетов полей могут быть определены основные параметры – собственные и взаимные индуктивности. Собственная индуктивность в статическом режиме вычисляется из формулы магнитной энергии:

_ 2 W

I ² ,               (5)

где I – ток обмотки катушки,

W _ j wdv

V                 (6)

W – энергия магнитного поля катушки, определяемая через объёмный интеграл по всей расчетной области от удельной плотности энергии w, которую в свою очередь можно определить из основных параметров поля:

w _

В частотной области (Time-Harmonic) среднее значение плотности энергии за период можно вычислить с помощью функций комплексного переменного:

1 Г r

W av _ 7 Re H • B

4 V J

кроме того, энергию магнитного поля можно определить путём интегрирования произведения вектора плотности тока и проекции векторного магнитного потенциала на вектор плотности тока:

— r

W _ 2 j J - A j dV j

^V J             .          (9)

причем направления векторов J и А J определяются направлением намотки катушек трансформатора. Ряд выполненных вычислительных экспериментов показал, что при вычислении энергии, а через неё и индуктивности наиболее целесообразно использовать формулы (9) дающую наиболее точный результат при использовании открытых границ.

В квазистатическом режиме как собственные, так и взаимные индуктивности можно определять аналогично, как это делается в реальных устройствах на основании опытов холостого хода и короткого замыкания. Индуктивность в этом случае можно вычислить по формуле: