Научные статьи \ Прикладные науки. Медицина. Технология \ Химическая технология. Химическая промышленность. Родственные отрасли \ Металлургия

Исследование и разработка программы термодинамического расчета восстановления хрома в руднотермических печах

Автор: Каскин Куат Камарович

Журнал: Вестник Южно-Уральского государственного университета. Серия: Металлургия @vestnik-susu-metallurgy

Статья в выпуске: 15 (274), 2012 года.

Бесплатный доступ

Разработана программа для термодинамического расчета восстановления хрома в руднотермических печах.

Термодинамический расчет, хромовая руда

Короткий адрес: https://sciup.org/147156726

IDR: 147156726 | УДК: 669.243

Текст научной статьи Исследование и разработка программы термодинамического расчета восстановления хрома в руднотермических печах

В работах [1, 2] приведены результаты выплавки хромоникелевого полупродукта, содержащего до 20 % Cr и около 10 % Ni, в полупромышленной рудовосстановительной печи мощностью 1,2 МВ∙А с использованием в шихте металлизо-ванных железорудных окатышей, хромовой руды, кокса и закиси никеля. По ходу опытных кампаний концентрация углерода в полупродукте, постепенно увеличиваясь, достигла 3,5–3,91 %, то есть превышала оптимальные его содержания в металле, в дальнейшем подвергаемом аргоно-кислородному рафинированию. В связи с этим возникла необходимость теоретически проанализировать полученные результаты и установить возможность выплавки в рудовосстановительных печах полупродукта с более низким содержанием углерода.

Рассматриваемая технология выплавки хромистого полупродукта в принципе отличается от технологии производства углеродистого феррохрома только содержанием хрома в шихте и готовом расплаве. Однако в теории ферросплавного производства восстановление хрома твердым углеродом, в частности на заключительной стадии, описывается только общей схемой ее уточнения термодинамическим анализом и количественными расчетами, поэтому целью настоящей работы является разработка компьютерной программы по восстановлению хрома.

В монографии [3] рассмотрены первые стадии твердофазного восстановления хромита FeO·Cr₂O₃, как основного минерала хромистых руд. Первоначально до металла восстанавливается только железо, а оксид хрома преобразуется в стойкие при высоких температурах карбиды Cr 23 C 6 , Cr 7 C 3 и Cr 3 C 3 .

Стандартная свободная энергия образования этих карбидов примерно одинаковая и в интервале

1403–1430 К парциальное давление равно 100 кПа (1 атм). Это позволяет принять для термодинамических расчетов любой карбид хрома. Авторы работы [3] отдают предпочтение карбиду Cr 7 C 3 , образующемуся в широком интервале концентраций хрома в сплаве. По их мнению, карбид Cr 7 C 3 взаимодействует с невосстановленным оксидом хрома Cr₂O₃ как при непосредственном контакте в нижней части колошника, так и в рудном слое, образующемся на границе шлака с металлом при наличии в шихте кусковой хромистой руды по реакции

1/30^ + 1/3C 7 C 3тв = 3[Cr] + CO. (1)

Естественно, что образующийся здесь металлический хром растворяется в жидком металле.

Присутствие тугоплавких металлов в рудном слое легко объяснимо. На первой стадии твердофазного восстановления хромита образуется металлическое железо. Однако сам процесс его образования в связи с необходимостью перестройки кристаллических решеток растягивается во времени [4] и по высоте колошника. Науглероженное и плавящееся железо стекает с кусков руды в горн печи, по пути только частично растворяя образовавшиеся карбиды хрома. При отсутствии рудного слоя процесс растворения карбидов в жидком металле, по-видимому, завершается в горне печи.

На границе рудного слоя с металлом в том же температурном интервале наряду с реакцией (1) не исключено и развитие реакции взаимодействия оксида хрома с растворенным в металлической фазе углеродом, контролируемой, как и в первом случае, парциальным давлением оксида углерода:

13 СГ 2 О 3ТВ + [C] i% = 2/3 [Cr] i% + CO, (2) т. е. протекание этих реакций взаимно увязано. Стандартная свободная энергия реакции (1) A G T

Таблица 1

Использованные экспериментальные данные

Проба Химический состав Температура, К [% C] по расчету [Ср] – [Сф], % % Cr % Ni % C 1-я кампания (пылеватая руда) 1 5,65 5,5 3,10 1753 8,13 5,03 2 9,45 8,5 3,42 1763 5,93 2,52 3 14,75 11,35 3,91 1773 4,42 0,51 2-я кампания (кусковая руда) 4 12,7 10,8 3,15 1723 4,45 1,30 5 14,3 9,55 3,42 1768 4,56 1,14 6 19,3 8,60 3,50 1823 4,28 0,78 при растворении хрома в металле, подсчитанная по исходным уравнениям [5], выражается уравнением:

A G T (1) = 87136 - 70,83 Т ,

1g K p ₀₎ = 3lg a Cr + 1g P CO =-- — +15,482.

Для реакции (2) по тем же данным A G T (2) = 58 770 - 35,57 Т , ^lg K p (2) = 2/3 ^lg a Cr ⁺ ^lg a C ^- ^lg P CO =

12 846

+ 8,212,

где a Cr и a C – активность хрома и углерода в расплаве.

Приравнивая выражение lg PCO по уравнениям (3) и (4), получим lg aC = [lg Kp(1) - lg Kp(2)] - 2,33lg aCr. (5)

Параметр взаимодействия eCCrr , судя по данным последних исследований [6], равен 3∙10–4, т. е. находится в пределах точности определения. Поэтому активность хрома aCr можно приравнять к его концентрации в сплаве. В области концентрации хрома до 20 %, наоборот, коэффициент активности углерода fC установлен достаточно точно и для сплавов Fe–Cr–Ni–C может быть представлен выражением lg fc = ec [% C] + eCr [% Cr] + eNi [% Ni] =

= 0,14[% C] - 0,024[% Cr] + 0,012[% Ni]. (6)

Приравнивая правые части уравнения (5) и выражения lg aC = lg [%C] + lg fC после подстановки в него значения fC из уравнения (6), получим уравнение для расчета равновесной концентрации углерода в металле lg[% C] + eC [% C] + eCr [% Cr] + eNi [% Ni] =

= [lg K_p (1) - lg K p ₍ 2) ] - 2,33lg a Cr . (7)

Всего на шихте с повышенным содержанием хрома (18 % по расчету) было проведено две полупромышленные кампании, отличавшиеся только использованием пылеватой (1-я кампания) или кусковой хромитовой руды (2-я кампания). Через каждые 3–4 часа выпускали из печи шлак и ме- талл, на желобе измеряли его температуру и загружали следующую порцию шихты. Высота слоя шихты на колошнике постепенно возрастала. Состав металла, его температура и расчетное содержание углерода в сплаве, подсчитанное на ЭВМ по уравнению (7) (табл. 1).

Приведенные результаты свидетельствуют о том, что по мере приближения к непрерывному процессу увеличивалась степень восстановления хрома и расчетные значения концентраций углерода в металле приближалась к фактическим. Относительное отклонение фактических и расчетных концентраций углерода в расплаве в этом случае 11,5 и 18,2 %, что подтверждает наш термодинамический расчет. При работе на пылевидных рудах в неустановившемся режиме работе печи нет и такого совпадения.

Таким образом, предложенный нами метод расчета применим только для тех условий, когда на границе металла и шлака, т. е. в рудном слое (рис. 1), присутствует непрореагировавший оксид хрома.

Рис. 1. Структура металла при выплавке хромистых сплавов: 1 – слой шихтовых материалов; 2 – полу-расплавленная масса; 3 – слой легкоплавкого шлака; 4 – слой плотного шлака; 5 – рудный слой; 6 – металл; 7 – «королек» металла; 8 – газовая полость

При использовании пылевидных руд типичный рудный слой отсутствует. Однако баланс хрома в шихте, в металле и в шлаке перед первым и вторым выпусками первой кампании обнаружил постепенное накопление в печи значительных количеств оксида хрома, не успевшего в наших условиях перейти на колошнике в карбид. Накопившийся к третьему выпуску в печи твердый оксид вступил в активное взаимодействие с углеродом металла, чем и объясняется совпадение в этом случае расчетных и экспериментальных данных.

Таким образом, высказанное предположение об одновременном развитии в рудном слое непрерывно действующих руднотермических печей процессов восстановления оксида Cr 2 O 3 до металла как за счет растворенного в нем углерода, так и в результате твердофазного взаимодействия оксида и карбидов хрома, достаточно обоснованно и позволяет количественно оценить активность и концентрацию углерода в металле.

Составляем таблицу для нахождения для реакции (1) изменения энтальпии, энтропии и температурных коэффициентов (табл. 2), затем производим термодинамический анализ.

В связи с этим предлагается программа, разработанная в среде Delphi 7 «Термодинамический расчет металлургических процессов» (рис. 2), которая позволяет: провести аналитический расчет в интервалах температур 400–3000 К с шагом в 50° с графическим изображением системы по данным расчета, что позволяет автоматизировать процесс расчета уравнений любых химических реакций, рассчитывая выход реакции.

На рис. 2, 3 представлена компьютерная программа термодинамического расчета.

Из анализа аналитических данных следует, что в температурном интервале 400–2400 К энергия Гиббса до 2100 К больше нуля, а константа равновесия меньше единицы. Следовательно, в температурном интервале 400–2100 К реакция твердофазного восстановления хрома находится в устойчивом равновесии.

На основе аналитического расчета определяем среднее Δ Н графическим методом.

В верхней части окна (рис. 4) расположен график зависимости ln K p = f (1/ T ), в нижней части среднее Δ Н аналитического и графического методов расчета для сравнения. Для того чтобы на графике увидеть температурную точку твердофазного восстановления хрома, выбираем режим «Анализ графика» .

В нижней части окна (табл. 3) показываются средние значения Δ Н и Δ S .

Таким образом, на основании аналитического и графического расчетов получаем уравнение свободной энергии

Δ G = 1 025 301,5 – 493,1429 T , Дж.

Из анализа (рис. 4, 5) следует, что реакция твердофазного восстановления хрома начинается при 1560 К, при расчете реакции (1) производим полный термодинамический анализ реакции (2).

Таблица 2

Реагент	A H 298 , кДж/моль	A S 298 , Дж/моль·К	Δ С р = f ( T ), кДж/моль∙К
Реагент	A H 298 , кДж/моль	A S 298 , Дж/моль·К	Δ a 0	Δ a 1 ·10³	Δ a –2 ·10^–5
9Cr	0	212,76	219,87	88,83	–33,12
3CO	–331,59	592,65	85,23	12,3	–1,38
∑ прод. реак	–331,59	805,41	305,1	101,13	–34,5
Cr 2 О 3	–1140,56	81,177	119,37	9,2	–15,65
Cr 7 C 3	–228,35	201,12	238,66	60,92	–42,4
∑ исх. реаг	–1368,91	282,29	358,03	70,12	–58,05
∑ прод – ∑ исх	1037,32	523,12	–52,93	31,01	23,55

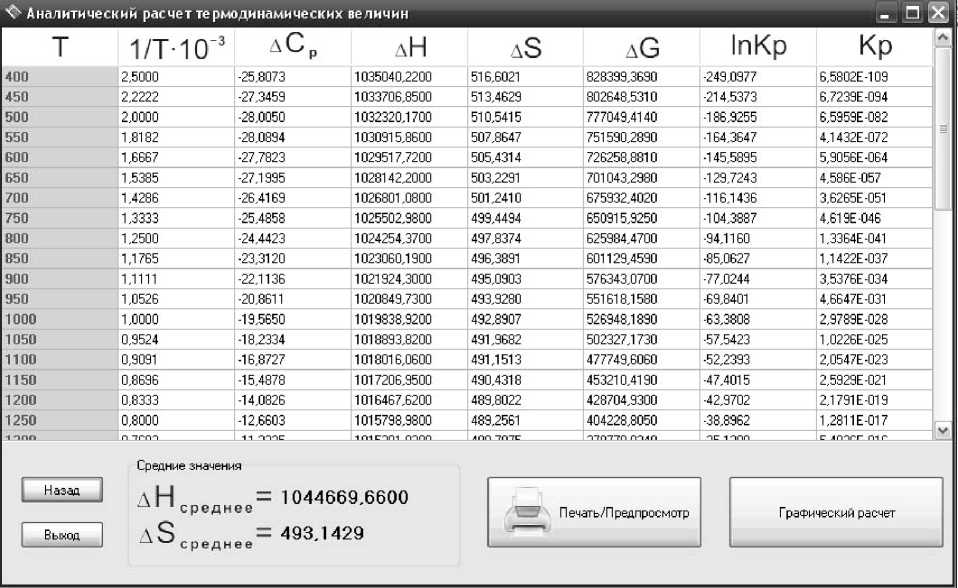
Рис. 4. Аналитический расчет термодинамических величин

Таблица 3

T	1/ T ∙10^–3	Δ C p	Δ H	Δ S	Δ G	ln K p	K p
400	2,5	–25,8073	1035040	516,6021	828397,8024	–249,217	6,8394E^–109
450	2,222222	–27,3459	1033707	513,4629	802679,2423	–214,649	6,01457E^–94
500	2	–28,005	1032320	510,5415	777048,841	–187,015	6,02919E^–82
550	1,818182	–28,0894	1030916	507,8647	751599,8741	–164,446	3,82E^–72
600	1,666667	–27,7823	1029518	505,4314	726256,0252	–145,659	5,50907E^–64
650	1,538462	–27,1995	1028142	503,2291	701039,0602	–129,786	4,31179E^–57
700	1,428571	–26,4169	1026801	501,241	675930,5618	–116,199	3,43038E^–51
750	1,333333	–25,4858	1025503	499,4494	650903,3898	–104,437	4,40151E^–46
800	1,25	–24,4423	1024254	497,8374	625981,0656	–94,1608	1,27785E^–41
850	1,176471	–23,312	1023060	496,3891	601105,4987	–85,1002	1,10012E^–37
900	1,111111	–22,1136	1021924	495,0903	576327,9454	–77,0595	3,41576E^–34
950	1,052632	–20,8611	1020850	493,93	551587,6895	–69,8699	4,52794E^–31
1000	1	–19,565	1019839	492,8907	526939,056	–63,4102	2,89258E^–28
1050	0,952381	–18,2334	1018894	491,9682	502300,553	–57,567	9,97665E^–26
1100	0,909091	–16,8727	1018016	491,1513	477745,9113	–52,2641	2,00447E^–23
1150	0,869565	–15,4878	1017207	490,4318	453186,4953	–47,4218	2,5408E^–21
1200	0,833333	–14,0826	1016468	489,8022	428703,2332	–42,9907	2,1349E^–19
1250	0,8	–12,6603	1015799	489,2561	404204,605	–38,9126	1,2603E^–17
1300	0,769231	–11,2235	1015202	488,7875	379774,8091	–35,1546	5,40213E^–16
1350	0,740741	–9,77432	1014677	488,3911	355317,2706	–31,6724	1,75725E^–14
1400	0,714286	–8,31447	1014225	488,062	330921,4106	–28,4443	4,43386E^–13
1450	0,689655	–6,8454	1013846	487,7958	306498,3428	–25,4366	8,97478E^–12
1500	0,666667	–5,36833	1013540	487,5886	282130,8235	–22,6338	1,47995E^–10
1550	0,645161	–3,88427	1013309	487,4368	257742,7206	–20,0103	2,04002E^–09
1600	0,625	–2,39408	1013152	487,337	233405,2544	–17,5545	2,3777E^–08
1650	0,606061	–0,89849	1013070	487,2862	209018,7213	–15,244	2,3966E^–07

Окончание табл. 3

T	1/ T ∙10^–3	Δ C p	Δ H	Δ S	Δ G	ln K p	^Kp
1700	0,588235	0,601879	1013062	487,2816	184676,7822	–13,0726	2,10202E^–06
1750	0,571429	2,10648	1013130	487,3208	160286,1771	–11,0219	1,63397E^–05
1800	0,555556	3,614852	1013273	487,4013	135934,837	–9,08777	0,00011304
1850	0,540541	5,126593	1013491	487,5209	111546,3235	–7,88312	0,000377056
1900	0,526316	6,641355	1013785	487,6777	87192,9432	–5,52239	0,003996304
1950	0,512821	8,158829	1014155	487,8699	62789,12418	–3,8748	0,020758582
2000	0,5	9,67875	1014601	488,0956	38416,05	–2,31144	0,099118912
2050	0,487805	11,20088	1015123	488,3533	13973,34038	–0,82025	0,440322297
2100	0,47619	12,72501	1015722	488,6415	–10443,521	–2,28612	0,101660536
2150	0,465116	14,25096	1016396	488,9588	–34907,22563	1,953781	7,055312321
2200	0,454545	15,77857	1017147	489,3039	–59348,463	3,246278	25,69453878
2250	0,444444	17,30769	1017974	489,6756	–83814,37175	4,482651	88,46891525
2300	0,434783	18,83818	1018877	490,0728	–108259,9083	5,664203	288,3580132
2350	0,425532	20,36994	1019858	490,4943	–132804,8005	6,800563	898,3531936
2400	0,416667	21,90285	1020914	490,9392	–157334,4152	7,888809	2667,266453

Рис. 3. Окно ввода данных

Рис. 2. Главное окно программы

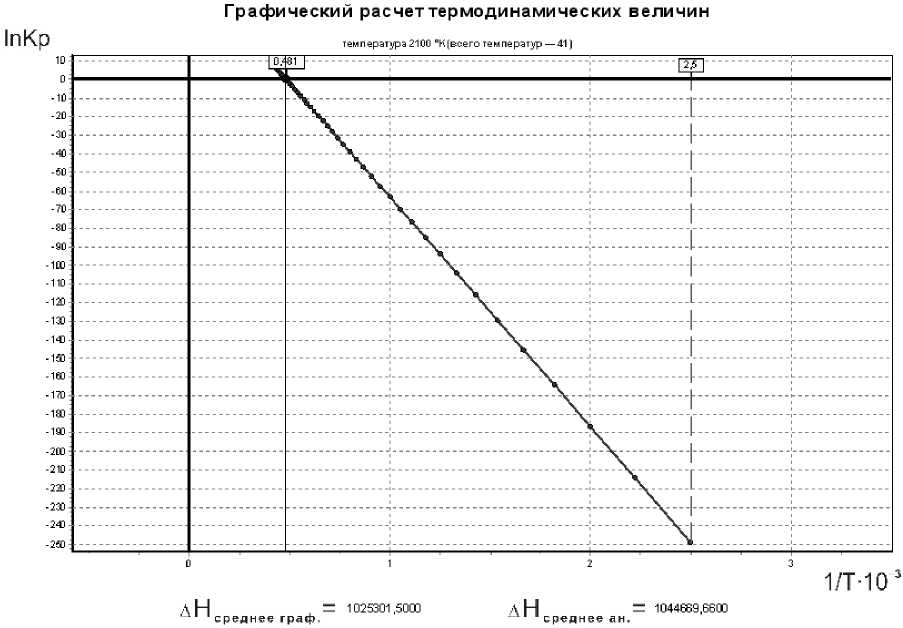
Рис. 5. Графический расчет

Из анализа аналитических данных следует, что в температурном интервале 400–2400 К энергия Гиббса до 1550 К больше нуля, а константа равновесия меньше единицы. Следовательно, в температурном интервале 400–1550 К реакция восстановления хрома находится в устойчивом равновесии.

Процесс восстановления хрома идет самопроизвольно только после 1550 К. Таким образом на основании аналитического и графического расчетов, получаем уравнение свободной энергии:

Δ G = 800 340,266 – 513,0249 T , Дж.

Из анализа (рис. 6) следует, что реакция твердофазного восстановления хрома начинается при 1560 К.

Таким образом, в настоящей работе в результате анализа технологических параметров выплавки хромоникелевого полупродукта с помощью разработанной компьютерной программы термо-

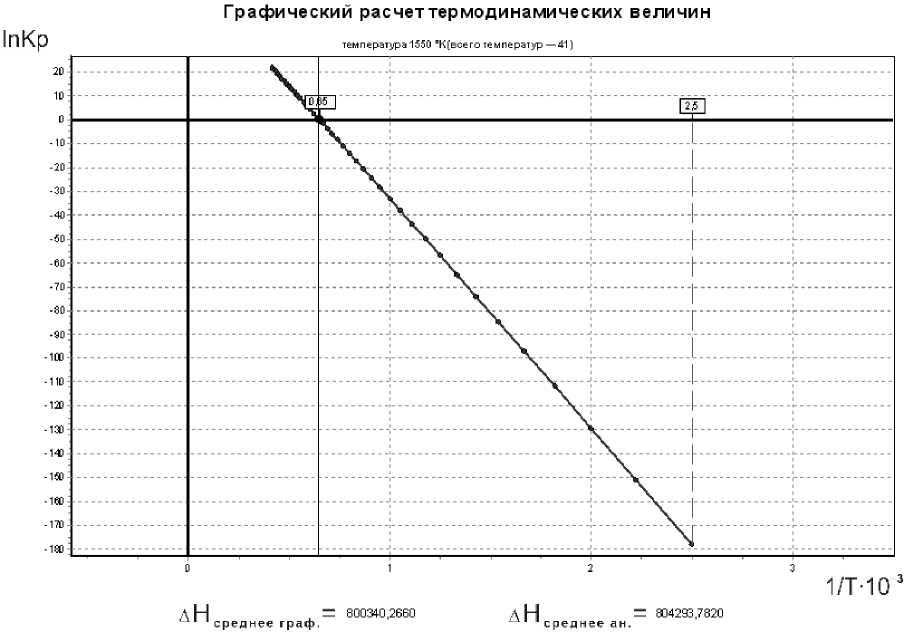
Рис. 6. Графический расчет

динамического расчета восстановления хрома установлено следующее.

1. Твердофазное восстановление хрома начинается при 1560°К согласно графического (рис. 5, 6) и термодинамического расчетов (см. рис. 2–4) компьютерной программы.
2. Высказанное предположение об одновременном развитии в рудном слое непрерывнодействующих процессов восстановления оксида до металла как за счет растворенного в нем углерода, так и в результате взаимодействия оксида и карбидов хрома достаточно обосновано.
3. Предложенные расчетные уравнения позволяют количественно оценить активность и концентрацию углерода в металле.
4. Установлено, что по мере приближения к непрерывному процессу увеличилась степень восстановления хрома, а расчетные значения концентрации углерода в металле на разработанной компьютерной программе приближались к фактическим.
5. Результаты, полученные с использованием данной программы, позволяют провести аналитический расчет в интервале температур 400–2000 К с шагом 50°, с графическим изображением системы по данным расчета, что позволяет автоматизировать процесс расчета уравнений любых химических реакций и произвести расчет выхода реакций.

Список литературы Исследование и разработка программы термодинамического расчета восстановления хрома в руднотермических печах

Кадарметов, А.Х. Выплавка хромоникелевого продукта непрерывным процессом/А.Х. Кадарметов, К.К. Каскин, А.Н. Учаев//Повышение качества и эффективности производства электростали: науч. тр. НИИМ. -Челябинск: Металлургия. Челябинское отделение, 1989.
Каскин, К.К. Разработка программы термодинамического расчета восстановления хрома в руднотермических печах/К.К. Каскин, Ч.А. Ахметов//Научно-технический прогресс в металлургии: тр. V Междунар. науч.-практ. конф. МОН РК. -Темиртау, 2009.
Гасик, М.И. Теория и технология производства ферросплавов/М.И. Гасик, Н.П. Лякишев, Б.И. Емлин. -М.: Металлургия, 1988. -784 с.
Гельд, П.В. Процессы высокотемпературного восстановления/П.В. Гельд, О.А. Есин. -Свердловск: Металлургиздат, 1957. -646 с.
Туркдоган, Е.Т. Физическая химия высокотемпературных процессов/Е.Т. Туркдоган. -М.: Металлургия, 1985. -344 с,
Григорян, В.А. Теоретические основы электросталеплавильных процессов/В.А. Григорян, Л.Н. Белянчиков, А.Я. Стомахин. -М.: Металлургия, 1979. -256 с.