Исследование и сравнение двойственных систем Е2/М/1 и М/Е2/1

B нaстоящее время не существует аналитических методов для точного определения характеристик системы массового обслуживания (СМО) общего вида G/M/1 или G/M/ m , в отличии от СМО общего вида М/G/1, для которой известна формула Полячека-Хинчина. Статья посвящена исследованию и сравнению двойственных СМО вида Е₂/M/1 и М/Е₂/1 с эрланговским и экспоненциальным входными распределениями. Первая система относятся к типу G/M/1, а вторая ‒ М/G/1.

По определению системы называются двойственными, когда закон распределения интервалов входного потока одной системы (первая позиция в трехпозиционной системе Кендалла) становится законом распределения времени обслуживания для другой системы (вторая позиция в указанной системе). Так, в системах Е2/M/1 и М/Е2/1 закон распределения входного потока Е2 первой системы становится законом обслуживания второй системы.

B теории СМО исследования G/M/1 особо актуальны в связи с тем, что до сих пор не существует решения в конечном виде для общего случая распределения интервалов входного потока. Метод спектрального разложения решения интегрального уравнения Линдли (ИУЛ) составляет важную часть теории систем G/G/1. Для записи интегрального ИУЛ введем следующие обозначения: W (у) - функция распределения вероятностей времени ожидания требования в очереди; С (и) = Р(U < и) - аналогичная функция для случайной величины U = х -t ; x - случайное время обслуживания требования; t - случайный интервал времени между поступлениями требований. Форма ИУЛ выглядит как

W ( У ) =

у,

J W ( у - и ) dC ( и ) , у >  0;

^{< -} "

0,            у <  0.

При кратком изложении метода спектрального разложения решения ИУЛ будем придерживаться подхода и символики автора теории СМО [2]. Для этого как А * ( s ) и В * ( s ) обозначим преобразования Лапласа функций плотности распределения интервалов между поступлениями и времени обслуживания соответственно.

Суть решения ИУЛ методом спектрального разложения состоит в нахождении для выражения А * ( - s ) • В * ( s ) - 1 представления в виде произведения двух множителей, которое давало бы рациональную функцию от ѕ . Следовательно, для нахождения закона распределения времени ожидания необходимо следующее спектральное разложение: А * ( - s ) • В * ( s ) - 1 = V + ( s ) / V _ ( s ) , где

V + ( s ) и V - ( s ) некоторые дробно-рациональные функции от s . Функции v₊ ( s ) и V - ( s ) должны удовлетворять следующим условиям согласно [2]: - для Re ( s ) >  0 функция v + ( s ) является аналитической без нулей в этой полуплоскости;

- для Re ( s ) < D функция v ( s ) является аналитической без нулей в этой полуплоскости, где D ‒ некоторая положительная константа, определяемая из условия: lim a ( t ) / e ^- Dt < да .

t ^да

Кроме того, функции v₊ ( s ) и V - ( s ) должны обладать следующими свойствами:

lim  VW = 1;

| s |^»,Re( s )> 0 s lim  Vti = -1.         (2)

| s |^» ,Re ( s ) < D s

Теперь остается применить метод спектрального разложения к рассматриваемым системам.

Постановка и решение задачи для системы Е2/М/1

В статье ставится задача качественного и количественного сравнения результатов для двойственных систем Е2/M/1 и М/Е2/1 по среднему времени ожидания в очереди. Для проведения сравнительного анализа приведем решения для обеих систем, полученные методом спектрального разложения ИУЛ.

В системе Е2/М/1 время поступления требований задана функцией плотности a (t ) = 4X2 te-2X t,(3)

преобразование Лапласа которой имеет вид

A* (s ) = | ^^1 .(4)

^{v 5} ( 2 X + s J

Время обслуживания распределено с функцией плотности b (t ) = ц e-ц t,(5)

а ее преобразование Лапласа имеет вид

B * (s ) = -H-.(6)

ц + s

Для применения метода спектрального разложения воспользуемся результатами [2] для систем общего вида G/M/1, к которым принадлежит система Е₂/М/1. Выражение для спектрального разложения решения ИУЛ для системы G / M/1 задается в виде [2]:

A ( - s ) * B * ( s ) - 1 =       =          (7)

V—( s)

цА* (-s)- s - ц s (s + s1) s (s + s1)        s + ц где s = -s1 - единственный отрицательный корень уравнения s + ц - цА* (-s) = 0. Выражение в первых скобках (5) не имеет ни плюсов, ни нулей в области Re(s) < 0 кроме s = 0 и s = -s1 [2]. Поэтому за функцию v+ (s) исходя из условий (1)(2) примем выражение во вторых скобках, так как его нули s = 0, s = -s1 и полюс s = - ц лежат в области Re(s) < 0, а за функцию v- (s) - выражение в первых скобках s (s + s)

V + ( s ) = ------^L; V - ( s ) = s + ц

- s ( s + s 1 )

*                .

s + ц-ц А ( - s )

Для окончательного построения функции

V - ( s ) подставим в ее выражение А* ( - s ) =

2 X + s J

Тогдафункция v - ( s ) приметвид

V - ^{( s} ) =

- s ( s + s 1 )

s + ц - ц [4 Х ² / ( 2 X - s ) 2 ]

- ( s + s 1 )( 2 X- s ) 2

= s ² + ( ц- 4 X ) s + 4 Х ( Х-ц ) =

- ( s + s 1 )( 2 X- s ) 2 _ (2 X- s ) 2 ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^I               ^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^H

( s + s 1 )( s - s ₂ )          s - s ₂

так как квадратное уравнение, полученное из знаменателя s ² + ( ц - 4 X ) s + 4 X ( X - ц ) = 0 , имеет один отрицательный корень:

- s 1 = - ( ц - 4 X ) / 2 - V [( ц- 4 X ) /2]² + 4 Х ( ц-Х ) и один положительный корень:

s ₂ = (4 X-ц )/2 + .j [ ( ц- 4 X ) /2]² + 4 Х ( ц-Х ) .

В случае стабильной системы при X < ц выполнено условие 4 Х ( ц-Х ) >  0. Теперь выполнение условий (1) и (2) метода спектрального разложения для построенных функций v₊ ( s ) и V - ( s ) очевидно. Это подтверждает и рисунок 1, где отображены нули и полюса отношения V₊ ( s ) / V - ( s ) на комплексной s- плоскости для исключения ошибок построения спектрального разложения. На рисунке 1 полюсы отмечены крестиками, а нули ‒ кружками.

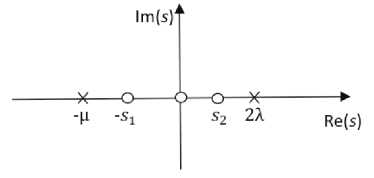
Рисунок 1. Нули и полюсы функции

V₊ ( s ) / V ( s ) для системы Е 2 /М/1

Далее по методике спектрального разложения найдем константу K :

K = lim ^^ = lim ^1 = У

I ^s l ' 0 s        H ' 0 s + ц ц

Построим функцию Ф₊ ( s ) , через которую найдем преобразование Лапласа функции плотности времени ожидания:

W * ( s ) = s * Ф₊( s ) = ^ il i +^I .

⁽ )          ^{+ (} ) ц ( s + s 1 )

Производная от функции W * ( s ) со знаком минус в точке s = 0 :

Тогда спектральное разложение решения ИУЛ для системы М/Е2/1 имеет вид

A * ( - s ) x B * ( s ) - 1 =

X <  2 ц --------x| ----------

X- s ( 2 ц + s

- 1 =

s [ s ² + ( 4 ц-X ) s + 4 ц ( ц-X ) J ( X- s )( 2 ц + s ) 2

Квадратный трехчлен в числителе разложения s2 + (4ц-X)s + 4(ц2-Xц), где 4ц(ц-X)> 0 и (4ц-X) > 0 при ц > X в случае стабильной системы, имеет два действительных отрицательных dW* (s)

ds

корня - s 1 , - s 2 :

- s 1 = - ( 4 ц-X ) /2 + [ ( 4 ц-X ) /2] 2 - 4 ц ( ц-X ) ,

_ s ₁ ц ( s + s j- s ( s + ц ) ц

.        Ц2(s + si)2

_ s ^² - S 1 ²ц _ 11

2 2■ ц s1

Тогда среднее время ожидания для системы Е /M/1:

W = 1/s1 -1/ц,(8)

где s 1 = ( ц - 4 X ) / 2 + ^|( ц 4 x ) 2| ' I 4 x ( ц x ), абсолютное значение корня - s 1 выражается через параметры распределений (3) и (4).

Для практического применения формулы (8) в качестве входных параметров для системы Е₂/М/1 будем использовать числовые характеристики распределений (3) и (4), а именно средние значения интервалов между поступлениями требований и времени обслуживания и коэффициенты вариаций этих интервалов: t_x = 1/ X , Т_ц= 1/ ц , c _X = 1 / V2, c _ц = 1. Задав эти числовые характеристики, методом моментов определяем параметры распределений (3)-(4) X , ц .

Решение для системы М/Е2/1 и его сравнение с формулой Полячека ‒ Хинчина

В этом случае функция плотности распределения для интервалов поступления имеет вид a (t ) = X e-x t,                    (9)

а для времени обслуживания b (t ) = 4ц2 te-2ц t.                 (10)

Преобразование Лапласа (9) и (10) есть

A* ( s ) = -^X- , B * ( s ) = |T 2M ■

X + s          ^ 2 ц + s J

- s ₂ = - ( 4 ц-X ) /2 - [ ( 4 ц-X ) /2]² - 4 ц ( ц-X ) .

Тогда окончательно спектральное разложение будет иметь вид:

V+M = s(£ +^,)( s + н ) .        (11)

^V - ( ^s ) ( X- s )( 2 ц + s )

Нули и полюсы этого разложения показаны на рисунке 2: полюсы отмечены крестиками, а нули ‒ кружками.

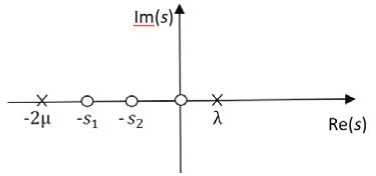
Рисунок 2. Нули и полюсы функции

V . ( s ) / V ( s ) для системы М/Е 2 /1

Исходя из правил построения функций v₊ ( s ) и V - ( s ) (1), (2) выбираем

, _х s ( s + s .)( s + s ₇)       , _{x л}

V₊ ( s ) = ⁽ _z ^{1 )(} _x2 ² ) , v _ ( s ) = X- s .

( 2 ц + s )

Необходимая для получения решения константа

V₊( ^s ) ss, K = lim--— = -Hr ^s ^ 0    s      4 ц ²

4 ц ( ц-X )

4 ц ²

= ^{1 -p} .

Далее строим функцию

Ф ₊ ( s ) = —— = ^{( 1 -p)( 2 ц + s} ) , V + ( s ) s ( s + 5 1 )( s + s 2 )

откуда следует, что преобразование Лапласа функции плотности времени ожидания в системе М/Е2/1

W * ( s ) = s * Ф₊ ( s ) =

( 1 -P )( 2 Ц + s ) 2 ( ^s + s )( ^s + ^s ₂ )

В связи с тем, что система М/Е2/1 относится к классу М/G/1, воспользуемся результатом для систем данного класса. Уравнение Полячека ‒ Хинчина для преобразования Лапласа функции плотности времени ожидания для системы М/G/1 имеет вид

загрузки, определяемый отношением среднего времени обслуживания к среднему интервалу поступлений р = т_ц / т_х . Для удобства вычислений принято нормированное время обслуживания в обеих системах т_ц = ц ^{- 1} = 1.

Таблица 1. Расчет среднего времени ожидания для систем Н2/M/1 и М/Н2/1

W * ( s ) =

^Hzp)_

s -X + X В *( s )

С учетом равенства преобразования Лапласа

В* (s ) =

2 ц

2 ц + s

Входные параметры	Среднее время ожидания
р	для системы Е2/М/1	для системы М/Е2/1
0,1	0.030	0,083
0,5	0,618	0,750
0,9	6,588	6,750

после его подстановки в (12) получим, что w* (s)=(1 р)(2ц+s) . (s + ^ )(s + s2 )

Тем самым подтверждено, что преобразование Лапласа функции плотности времени ожидания для системы М/G/1 в случае СМО М/Е2/1 совпадает с выражением (11).

Среднее время ожидания в системе М/G/1 д ается формулой Полячека ‒ Хинчина [2]:

- X T 2

W = , X ,

• ² ( 1 -P )

  
  

где λ ‒ интенсивность входно г о потока, ρ ‒ коэффициент загрузки системы, т 2 - второй начальный момент времени обслуживания. Для распределения Е₂ вто р ой начальный момент времени обслуживания т Ц = 3 / (2 ц ²) , тогда среднее время ожидания в системе М/E₂/1:

W =

3 р

4 ц ( 1 -р ) ‘

Сравнительные расчеты среднего времени ожидания для систем Е2/М/1 и

М/Е2/1

Для того, чтобы лучше оценить количественную разницу между рассматриваемыми двойственными системами, проведем вычислительные эксперименты для среднего времени ожидания по формулам (1), (7) и (11) соответ-cтвенно. Выше было отмечено, что формулы (1) и (7) дают идентичные результаты.

В таблице 1 приведены результаты расчетов для рассмотренных систем для случаев малой загрузки системы ρ = 0,1; средней загрузки ρ = 0,5 и высокой загрузки ρ = 0,9. Здесь ρ ‒ коэффициент

Данные таблицы 1 свидетельствуют о незначительном различии рассмотренных двойственных систем в связи с сравнительно небольшими коэффициентами вариаций используемых законов распределений. В случае других законов распределений двойственные системы G/M/1 и М/G/1 будут давать достаточно отличающиеся результаты.

Результаты расчетов хорошо согласуются с данными [9].

Заключение

Основная характеристика для СМО ‒ это среднее время ожидания в очереди, так как все остальные характеристики։ время задержки, средняя длина очереди, количество требований в системе и др. являются производными от нее.

Результаты по среднему времени ожидания в очереди для систем Е2/M/1 и М/Е2/1 получены одним и тем же методом спектрального разложения решения ИУЛ [1]. Полученные результаты показывают, насколько отличаются эти две двой-cтвенные системы и свидетельствуют о незначительном различии рассмотренных двойственных систем в связи со сравнительно небольшими коэффициентами вариаций используемых законов распределений.