Исследование и сравнение пары двойственных систем с гиперэрланговскими и экспоненциальными распределениями

Статья посвящена анализу систем массового обслуживания (СМО) НЕ2/М/1 и М/НЕ2/1 с ги-перэрланговским (НЕ2) и экспоненциальным (М) входными распределениями. В открытом доступе автору не удалось обнаружить результаты для среднего времени ожидания требований в очереди в таких СМО. Как известно из теории массового обслуживания, среднее время ожидания является главной характеристикой для любых СМО. По этой характеристике, например, оценивают задержки пакетов в сетях пакетной коммутации при их моделировании с помощью СМО. Рассматриваемые СМО относятся к типу G/M/1 М/G/l соответственно.

Исследования таких систем актуальны в связи с тем, что они активно используются в современной теории телетрафика. Законы распределений Вейбулла или гамма наиболее общего вида, которые обеспечивают диапазон изменения коэффициентов вариаций от 0 до ю в зависимости от величины их параметров, не позволяют их использовать в теории массового обслуживания. Поэтому остается использовать другие частные законы распределений.

Метод спектрального разложения решения интегрального уравнения Линдли (ПУЛ) в теории систем массового обслуживания G/G/1 зани мает важное место. Для записи ПУЛ, а также при рассмотрении метода спектрального разложения решения ПУЛ будем использовать стандартные обозначения [1]. Через 4*(s) и B*(s) обозначим преобразования Лапласа функций плотности распределения интервалов между поступлениями и времени обслуживания соответственно. Суть решения ПУЛ методом спектрального разложения состоит в нахождении для выражения 4*(-s)-6*(s)-l представления в виде произведения двух множителей, которое давало бы рациональную функцию от s. Следовательно, для нахождения закона распределения времени ожидания необходимо следующее спектральное разложение: Л*(-»)• S*(s)-l = ^+(s)/\|/_(s), где ш+(«) и v|/_(s) некоторые дробно-рациональные функции от s, удовлетворяющие специальным условиям согласно [1], которые здесь опускаем.

Постановка задачи

В статье ставится задача вывода формул для среднего времени ожидания для рассматриваемых систем НЕ₂/М/1 и М/НЕ₂/1, а также подтверждения адекватности построенных математических моделей путем численного моделирования в пакете Mathcad. Вывод решения для среднего времени ожидания проводится методом спектрального разложения решения ИУЛ, как это показано в [2-6].

Решение для системы НЕ2/М/1

В системе НЕ2/М/1 интервалы времени между поступлениями требований заданы функцией плотности aU^ApA^2'2 +А^\-р^(D преобразование Лапласа которой имеет вид: /         \2           /\2

А ^ = р ~• (2) s + 2Aj jJ

Время обслуживания распределено с функцией плотности

Ь^ = Ц^"'.(3)

а ее преобразование Лапласа имеет вид

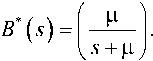
Тогда спектральное разложение решения ИУЛ для системы НЕ/М/1 А *(-s) В *(з)-1 = ЧЛ (⁵) / ^-(s) примет вид

Md

Md

Г 2Х )

р\---—

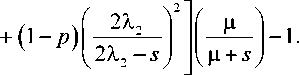
Первый сомножитель (5) после соответствующих выкладок представим в виде

Р

' 2Х, \ v2Х, -sj

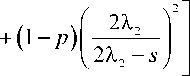
aQ — axs + a2s2

(2X, -s)2(2X2-s)2’ где промежуточные параметры a0 = 16X^X3, ax = 1 бХ^з^Х! + (1 — p^X2"\,

Продолжая разложение (5), получим

V+t⁵)-   4ц² (а₀ — a_xs + a₂s²)

Md (2Х, - s)2 (2Х2 - s)2 (ц + s)

(2Xj - з)² (2X₂ - s)² (ц + s)

(21, - s)2 (2X2 - s)2 (p + 3)

_ -s(s + s, )(s + s₂ )(s - s₃ )(s - s₄) ^X_x - s)² (2X₂ - 5)" (ц + s)

Окончательно спектральное разложение решения ИУЛ для системы НЕ2/М/1 имеет вид

У₊ СО ₌ -s(s + V X» + s₂ Xs - s₃ )(з - з₄)

МО (2X,-з)2(2Х2-з)2(ц + з)

Исследование многочлена в числителе разложения (6) и определение его корней является основным моментом метода спектрального разложения решения ИУЛ. Многочлен четвертой степени в числителе разложения

5⁴ + c₃s³ + c₂s² + c_xs + с₀           (7)

с коэффициентами с0 = ахр + 16Х1Х2[Х]Х2 -ц(Х( +Х2)], сх = 4ц(/.; + 4ХД2 + X-) — ISX^Xx^X^ + Х2) — гг2ц, с. = 4(Х( + Х2) +16Xj Х2 — 4ц(Х1 + Х2), с3 = ц-4(Х1 + Х2)

в случае стабильной системы имеет один действительный отрицательный корень и три положительных корня (либо вместо последних один действительный положительный и два комплексно-сопряженных с положительной вещественной частью). Эти коэффициенты сформированы с помощью символьных операций Mathcad и выражаются через параметры распределений (1) и (3), которые предстоит еще определить.

Далее строим рациональные функции ЧХ (d и ЧО (d: ЧЧС5) = 5(5 + 5i) /(Ц + 5)> так как нули многочлена (6): з = 0, з = -з, и полюс з = -ц лежат в области Re(s) < 0, а функция

^-М = -

(2Х1-з)2(2Х2-з)2

(з-з2)(з-з3)(з-з4)’ так как ее нули и полюсы лежат в области Re(s) > D, как того требует метод спектрального разложения.

Далее по методике спектрального разложения найдем константу К^-.

+       3,

К =

5      5-»0 (з + ц) Ц где 3] - абсолютное значение отрицательного корня -з,. Постоянная X определяет вероятность того, что поступающее в систему требование застает ее свободной.

Для нахождения преобразования Лапласа функции плотности времени ожидания построим функцию

Ф₊м ₌ ^М₌ ^(^+Ю

⁺ ЧЧ^) зц(з + 3])

Отсюда преобразование Лапласа функции плотности времени ожидания Л^*(з) = з • Ф+ (з) будет равно

Для нахождения среднего времени ожидания найдем производную от функции W* (з) со знаком минус в точке з = 0:

^‘(s), _ 1 1 ,     L=0 —'

as5] м

Окончательно среднее время ожидания для системы НЕ2/М/1

^-I/s.-I/m.(9)

Выражение (8) для преобразования Лапласа функции плотности времени ожидания позволяет определить также моменты высших порядков времени ожидания, а именно вторая производная от преобразования (8) в точке 5 = 0 дает второй начальный момент времени ожидания, что позволяет определить дисперсию времени ожидания. В стандарте [9] джиттер (дрожание задержки) в телекоммуникациях определен как колебание времени ожидания вокруг его среднего значения. Тогда джиттер можно определить через дисперсию времени ожидания. При анализе трафика, чувствительного к задержкам, это будет важным подспорьем.

Для использования формулы (9) при расчетах необходимо знать числовые характеристики распределения (1). Для распределения (3) они легко определяются. Через числовые характеристики будем определять неизвестные параметры распределений (1) и (3) методом моментов. Для этого воспользуемся основным свойством преобразований Лапласа (2) и (4) воспроизведения моментов и запишем первые два начальных момента для распределения (1):

- Р (!~Р)

1 Х2 ’

7₌зГр (i^a) ^х 2р( х²

Рассматривая равенства (10) как форму записи метода моментов, найдем неизвестные параметры распределения (1) X,, Х₂, р. Так как система двух уравнений (10) является недоопределенной, к ней добавим в качестве недостающего уравнения выражение для квадрата коэффициента вариации:

С² = ^? 2 2 ■            (^ы)

(Ч)"

Выбираем значения параметров X,, X, так, чтобы они были решениями первого уравнения (10)

Х,=2^/т„ Х2=2(1-р)/т,    (12)

и потребуем выполнения условия (11) [2; 3]. Подставив выражения (12) в (11), получим уравнение четвертой степени относительно неизвестного параметра р-. /)(1-/))[8(1 + с^)/>2-- 8(1 + с2 Д? + 3] = 0. Отбросив тривиальные решения р = 0 и р=\, получим квадратное уравнение следующего вида: 8(1 + с22р2 - 8(1 + с^Р + 3 = 0, решив которое выберем для однозначности больший корень для параметрар;

1 N 8(1 + с{)

Отсюда следует, что коэффициент вариации с_х > 1 / V2. Теперь, подставив (13) в (12), определяем все три неизвестных параметра Х_р Х₂, р распределения (1) [2].

Для распределения (3) числовые характеристики равны тц = 1 / ц, сц = 1 [4]. Аналогичную аппроксимацию законов распределений с использованием начальных моментов можно увидеть в [7; 8].

Решение для системы М/НЕ2/1

Для двойственной системы законы распределения входного потока и времени обслуживания задаются функциями плотности а^ = Хе""и,              (14)

b^ = ^qy?_vte"^1V4t + 4(1 - q^y^e”²^.     (15)

Запишем преобразования Лапласа функций (14), (15):

В*^ = q

2ц,

5 +2ц,

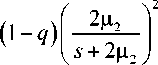
В этом случае выражение для спектрального разложения решения ПУЛ примет следующий вид:

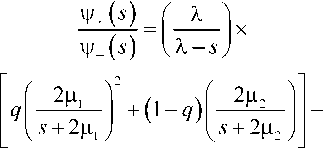
Поступив аналогично с системой НЕ2/М/1 и опустив некоторые выкладки, выпишем многочлен четвертой степени в числителе разложения (16):

s⁴ + d2 + d.2 + d_}s + d₀        (17)

с коэффициентами d0 =й1Х + 16ц1ц2[ц1ц2-Х(ц1 + ц2)], d, = 16|и1р.2(]и1 + ц2)-4Х(ц( + 4Ц]Ц2 + ц2 ) + 62Х, d2 = 4(ц2 + ц)) +1 бц^ - 4Х(ц, + ц2), d3 = 4(pt + ц2) - X.

Многочлен (17) с положительными коэффициентами имеет четыре действительных отрицательных корня либо два действительных отрицательных корня и два комплексно-сопряженных корня с отрицательными вещественными частя- ми. Тогда окончательно спектральное разложение решения ИУЛ для системы М/НЕ2/1 имеет вид

V-W (2ц, + s)2 (2ц2 + s)2 (X-s) ’ где через -о,, -о2, -о3, —п4 обозначены для удобства отрицательные корни многочлена (17).

Далее по правилам спектрального разложения строим функции ^(s) и V7-^):

z х _ s(s + ct₁)(s + ct₂)(s + ct₃)(s + (t₄)

ЧЕ v / —        /        \7 / 7г ’

(2ц,+д) (2ц2+д)

Ч'-С⁵) -X-s.

Константа спектрального разложения

s

_{= и} (s + ctJCsjHoJCs + cJCs + oJ ₌ (2p,+s)²(2p₂+s)²

_ ^1^2^3^4 1бц^ц=

Отсюда преобразование Лапласа функции плотности времени ожидания будет равно

W*^ =

<т,о2ст3ст4 (2ц, + s)2 (2ц2 + s)"       (19)

16ц(ц2 (5 + СУ, )(s + 4) ’ а среднее время ожидания ds при s = 0:

- 1      1      1      1      11

W = — + — + — +-----.(20)

су,   g2   о3   а4   ц,ц

Определение неизвестных параметров распределений (14) и (15) будет аналогично для системы НЕ₂/М/1. Параметр q аналогично р будет 1₊ / 2(1 ₊ с^)-3

N 80+ с2) ’ подставив его в выражения Ц]=2^/тц, ц2 = = 2(1-^)/тц, найдем все неизвестные параметры распределения (15).

Результаты численного моделирования

Ниже в таблице приведены данные расчетов среднего времени ожидания для систем НЕ₂/М/1 и М/НЕ₂/1 для случаев малой, средней и высокой нагрузки р = 0,1; 0,5; 0,9. Заметим, что первая система определена для коэффициентов вариаций интервалов поступления и обслуживания с_х > 1 / V2 и с = 1, а вторая - для с, = 1 и

Коэффициент загрузки р определяется отношением средних интервалов р = ¥ / тх. Результаты, приведенные в таблице, получены для нормированного времени обслуживания т = 1. Данные таблицы свидетельствуют о незначительном различии сравниваемых систем в случае высоких нагрузок и более значительных расхождениях -при средних и малых нагрузках. Двойственные системы этим и отличаются друг от друга.

Результаты расчетов для системы хорошо согласуются с данными [10] в той области изменения параметров, при которых применимы данные системы.

Заключение

В работе получены спектральные разложения решения ИУЛ для систем НЕ2/М/1 и М/НЕ,/1, а через них выведены расчетные формулы для среднего времени ожидания требований в очереди для этих систем. Эти формулы дополняют известную незавершенную формулу теории массового обслуживания для среднего времени ожидания систем типа G/G/1.

Известно, что среднее время ожидания требований в очереди является главной характеристикой СМО, так как все остальные характеристики: средняя задержка, средняя длина очереди, среднее количество требований в системе и другие определяются через среднее время ожидания.

Адекватность полученных результатов обеспечена корректным использованием классического метода спектрального разложения, а проведенные вычислительные эксперименты только подтверждают данный факт.

Таблица. Результаты экспериментов для СМО НЕ2/М/1

и М/НЕ2/1

Входные параметры			Среднее время ожидания
P	А	G	для системы НЕ2/М/1	ДЛЯ системы М/НЕ2/1
0,1	0,71	0,71	0,03	0,09
	2	2	0,08	0,28
	4	4	0,10	0,94
	8	8	0,11	3,61
0,5	0,71	0,71	0,62	0,75
	2	2	2,00	2,50
	4	4	4,62	8,50
	8	8	10,15	32,50
0,9	0,71	0,71	6,61	6,77
	2	2	22,59	22,50
	4	4	77,28	76,50
	8	8	295,96	292,50