Исследование идентифицирующих свойств нечеткого многослойного персептрона

Решение задачи идентификации является одним из важнейших применений нейронных сетей [1].

Задача идентификации представляет собой задачу отнесения образца к одному из нескольких попарно не пересекающихся множеств. Примером таких задач может быть, например, задача определения кредитоспособности клиента банка, медицинские задачи, в которых необходимо определить, например, исход заболевания, решение задач управления портфелем ценных бумаг (продать, купить или “придержать” акции в зависимости от ситуации на рынке), задача определения жизнеспособных и склонных к банкротству фирм.

Для исследования идентифицирующих свойств была разработана автоматизированная система, реализующая нечеткий многослойный персептрон, а также алгоритмы обучения данной нейронной сети.

С учётом ярко выраженной двухкомпонентной структуры гибридной сети для её обучения применялся алгоритм, состоящий из двух этапов.

На первом этапе обучения использовался алгоритм нечеткой самоорганизации C-means или K-means.

Рассмотрим алгоритм C-means.

Подаваемый на вход сети вектор x будет принадлежать к различным группам, представляемым центрами c_i , в степени u it , причем 0 <  u it <  1 , а суммарная степень принадлежности ко всем группам, очевидно, равна единице [2].

Поэтому:

M

Е u « = ¹ .

i = 1

Первичная инициализация центров функции Гаусса:

P

Ек)mx

t = 1

P

EWm t=1

Функцию погрешности можно определить как сумму частных погрешностей принадлежности к центрам c i с учетом степени принадлежности u_it . Следовательно:

MP e = ЕЕ Wmk- *.Г    (3)

i = 1 t = 1

Новые значения степеней принадлежности:

u it =                    1 .

M ( 2 Л m -1

E —it k=1 < d kt )

Рассмотрим второй использованный алгоритм нечеткой самоорганизации K – means.

Главной концепцией алгоритма K – means является центроид, или центр масс. В кластеризации данных центр масс набора последовательностей данных — это одна из последовательностей, которая является наиболее репрезентативной в группе.

На рис. 1 представлен пример самоорганизации входных данных. Элемент данных, заключенный в окружность, в каждом наборе, является центром масс этого набора [3].

В конечном счете, цель данного алгоритма – это минимизация целевой функции:

kn

J = ЕЕ1 \j-- ,Г.

j = 1 i = 1

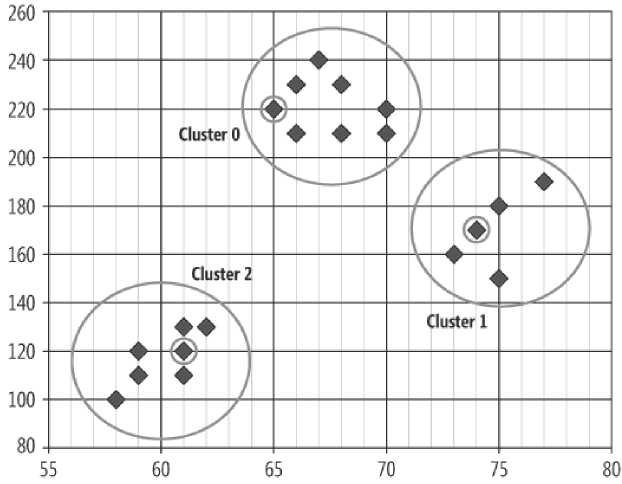
Рис. 1. Пример самоорганизации входных данных

На втором этапе обучения возможно использование алгоритма обратного распространения ошибки или эвристического алгоритма.

Алгоритм обратного распространения ошибки сводится к корректировке синоптических связей по формулам [4]:

w ( t ₊ 1 ) = w ( t ) + Д w (6), где Д w = n p ( w ) (7)

Обучение многослойной сети с применением градиентных методов требует определения вектора градиента относительно весов всех слоев сети, что необходимо для правильного выбора направления p(w).

Простой эвристический алгоритм, демонстрирующий высокую эффективность обучения, -это алгоритм М. Ридмиллера и Х. Брауна, называемый RPROP [5]. В этом алгоритме при уточнении весов учитывается только знак градиентной составляющей, а ее значение игнорируется:

( Э E ( w ( t ))

Д w , ( t ) = - П , ( t )sgn I ------------- ( ^{Э w},

Коэффициент обучения подбирается индивидуально для каждого веса w , с учетом изменения значения градиента:

min (ап , (t ^{- 1} )П max ) для S_M(t)S_M(t ^{- 1} )> 0 max (b n , ^{(t - 1} Л п m,n ) для S_q(t⁾S_q(^{t - 1} )< 0

П, (t - 1) в остальных случаях п ^t) = { {

Э E ( w ( t ))

где S i, ( t ) =            , a и b - константы: a=1.2;

Э w, b=0.5. Минимальное и максимальное значения коэффициента обучения составляют nmin = 10 -6 и Пmax = 50. Функция sgn( ) принимает значение, равное знаку градиента.

В начале работы системы, можно загрузить из файла ранее созданную нейронную сеть или создать новую. На рис. 2 представлена форма создания новой нейронной сети [6].

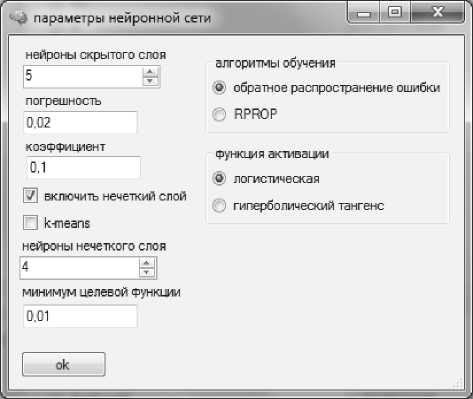
Рис. 2. Создание новой нейронной сети

Пользователь может выбрать для персептрона функцию активации его нейронов, алгоритм обучения, коэффициент, погрешность обучения и количество нейронов в скрытом слое. Также возможно подключить нечеткий слой и тогда нейронная сеть будет работать как нечеткий многослойный персептрон. Если не подключать нечеткий слой, то сеть будет работать, как обычный многослойный персептрон, что может негативно

Таблица 1. Зависимость качества идентификации от модели нейронной сети и алгоритма обучения

	Нечеткий многослойный персептрон	Многослойный персептрон
Алгоритм обратного распространения ошибки	116	107
Эвристический алгоритм обучения RPROP	130	113

Таблица 2. Зависимость качества идентификации от функции активации нейронов

	Логистическая ф ункция активации	Функция актив ации гиперболический тангенс
Количес тво правильно идентифицированных классов	124	129

Таблица 3. Зависимость качества идентификации от алгоритма обучения нечеткого слоя

K – means C – means Количес тво правиль но идентифицированных классов 119 122 сказаться на идентифицирующих способностях сети [7].

Для двух идентифицируемых классов было сгенерировано 200 тестовых примеров. В таб. 1 представлено сравнение идентифицирующих способностей нейронной сети с включенным и отключенным нечетким слоем, а также сравнение различных алгоритмов обучения для многослойного персептрона.

Как видно из таб. 1, наиболее хорошими идентифицирующими способностями обладает гибридная нейронная сеть модели нечеткий многослойный персептрон.

Эвристические алгоритмы обладают более высокой эффективностью при обучении нейронной сети.

При отключенном нечетком слое эвристический алгоритм обучения RPROP обладает более высокой эффективностью, однако общее качество идентификации сети ухудшилось.

Качество идентификации может зависеть и от функции активации нейронов. В таблице 2 для 200 тестовых выборок представлена зависимость качества идентификации нечеткого многослойного персептрона от функций активации нейронов персептрона.

Как видно из таб. 2, функция активации гиперболический тангенс позволяет нейронной сети приобрести более высокие идентифицирующие свойства. Однако стоит заметить, что большой разницы в качестве идентификации при разных функция активации не наблюдается.

Качество идентификации может зависеть от алгоритма обучения нечеткого слоя. В таб. 3 для 200 тестовых выборок представлена зависимость качества идентификации нечеткого многослойного персептрона от выбора алгоритма обучения нечеткого слоя.

Как видно из таб. 3, наиболее хорошие идентифицирующие свойства сеть приобретает при использовании алгоритма C – means.

Исследования показали, что наилучшими идентифицирующими свойствами обладает сеть модели нечеткий многослойный персептрон, для обучения которого применялся эвристический алгоритм RPROP.