Исследование импульсного воздействия на гидролитосферные процессы
Автор: Шевцов М.М., Каленчук Е.В.
Журнал: Форум молодых ученых @forum-nauka
Статья в выпуске: 2 (30), 2019 года.
Бесплатный доступ
В статье рассматривается импульсное воздействие на гидролитосферные процессы. Математическая модель описана для нескольких пластов, получены графики переходных процессов, а также проведена оценка влияния импульсного воздействия дебита скважины на понижение уровня минеральных вод в водоносных пластах.
Гидролитосферные процессы, добывающие скважины, оптимизация, математические модели
Короткий адрес: https://sciup.org/140285703
IDR: 140285703
Текст научной статьи Исследование импульсного воздействия на гидролитосферные процессы
Территория Кавказских Минеральных Вод (КМВ) - это особо охраняемый эколого-курортного регион России. Благодаря своим целебным свойствам, минеральные воды региона КМВ по праву признаны не только в нашей стране, но и за её пределами. Однако по данным государственного мониторинга подземных вод в регионе отмечается ухудшение качества минеральных вод. Неблагоприятная техногенная ситуация с поверхностными и грунтовыми водами, не утилизированные отходы, интенсивная добыча полезных ископаемых - вот основные причины антропогенного воздействия на гидролитосферу, вследствие чего происходит загрязнение водных ресурсов и их истощение.
В результате из баланса потребления выведены некоторые разновидности ценнейших питьевых и бальнеологических вод, и поэтому проблема рационального использования природного гидроминерального сырья в области добычи требует применения новых технологий, обеспечивающих экологическую и безопасную эксплуатацию гидроминеральной базы при возрастающих потребностях в этом сырье.
Используя принципы и методы систем с сосредоточенными параметрами, рассмотрим применение импульсного режима эксплуатации скважины и его воздействие на гидроминеральный пласт.
Управление технологическими процессами добычи гидроминерального сырья предполагает решение следующих задач: совершенствование методов определения гидравлических параметров водоносных горизонтов; совершенствование методов построения математических моделей рассматриваемых процессов; совершенствование принципов и методов управления этими процессами.
Основные этапы методики . Построим математическую модель части минерального водяного пласта. Входным воздействием на объект управления в этом случае будет служить дебит добывающей скважины. Функцией выхода - понижение уровня давления в зоне расположения скважины.
Вследствие того, что определение гидравлических параметров водоносного горизонта сложная и дорогостоящая задача, то аппроксимация динамических и статических характеристик объекта будет проводиться с использованием экспериментальных данных.
Исследуя влияние импульсного воздействия на добывающую скважину, рассмотрим Кисловодское месторождение, схема которого приведена на рисунке 1. При этом имеется возможность либо физического эксперимента на реальном объекте, либо численного эксперимента с использованием математической модели объекта.
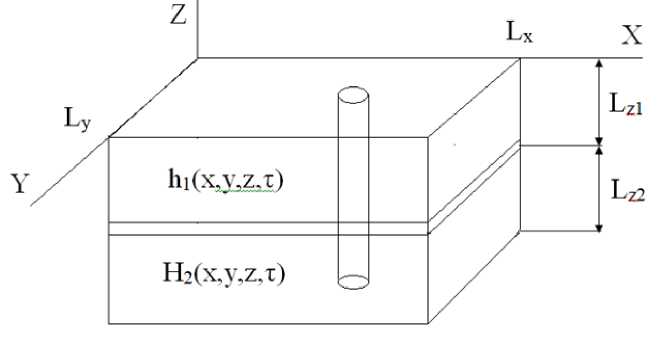
Рис.1 Схема месторождения
Математическая модель объекта.
Грунтовые воды
д h 1 (x,y,z, т ) =
дт
д 2h i (x, y, z, т ) д 2h i (x, y, z, т ) д 2h i (x, y, z, т )
1,x 2 + k1,y 2 + k1,z „ 2 ’ дx ду дz1
0 < x < L -0 < y < L -0 < z < L, x y Z i
д H 2( x , y , z , т )
дт
П 2
k 2, x к
Общий нарзан д2 H((x, y, z ,т ) д2 H((x, y, z ,т)
a x 2 + k 2->' a y■2 + k 2z
+ V( т ) • 5 ( x 0 , y 0 , z 0 );
д H(xx , y , z, т )
д2г 2
+
0 < x < L -0 < y < L -0 < z < L x y Z( где:
h 1 – уровень давления грунтовых вод;
Н2 – уровень давления водоносном горизонте;
коэффициенты фильтрации в декартовой системе координат:
k1x = 0,192 м /сут., k1y== 0,192 м /сут., k1z = 0,0195 м /сут., k2x = 0,19 м /сут., k2y = 0,19 м /сут., k2,z = 0,019 м /сут.;
П2= 0.00101/м.- упругоемкость пласта;
V(t) -понижение давления, вызванное воздействием добывающей скважины;
V(t) = Q*K;
где Q - дебит добывающей скважины, K - коэффициент усиления;
5(x0, y0, z0) - функция, равная единице, при условии, что x = x0, y = y0, z = z0, и равная нулю в остальных случаях;
x, y, z - пространственные координаты;
т-время.
Граничные условия (условия Дарси) между пластами зададим в виде: Грунтовые воды - верхний пласт hi (x,y,LZ], т) = h1 (x,y,LZ], т)+ bi -(Н2 (x,y,0, т)- h1 (x,y,LZ], т)), Н2 (x, y,0, т) = Н2 (x,y,° т)- Ь1 • (н2 (x, y,0,т)- hi (x,y,Lzt,т)) .
где b i = 0,00003 сут.-1-параметр перетекания.
Нижняя граница пласта:
д Н 2 ( х , y , L^ , т ) / д z = 0
Боковые грани: hi (0, y, z, т ) = h^; Н2 (0, y, z, т ) = Н2,о, дh (Lx, y, z, т) / дх = 0; дН2 (Lx, y, z, т) / дх = 0.
При формировании граничных условий по координате у, допустим, что мощность пластов такова, что возмущения от заборной скважины не влияют на состояние на границах пласта в точках:
h i ( х ,0, z , т ) = h i ( х , L y , z , т ) = h i,0 ,
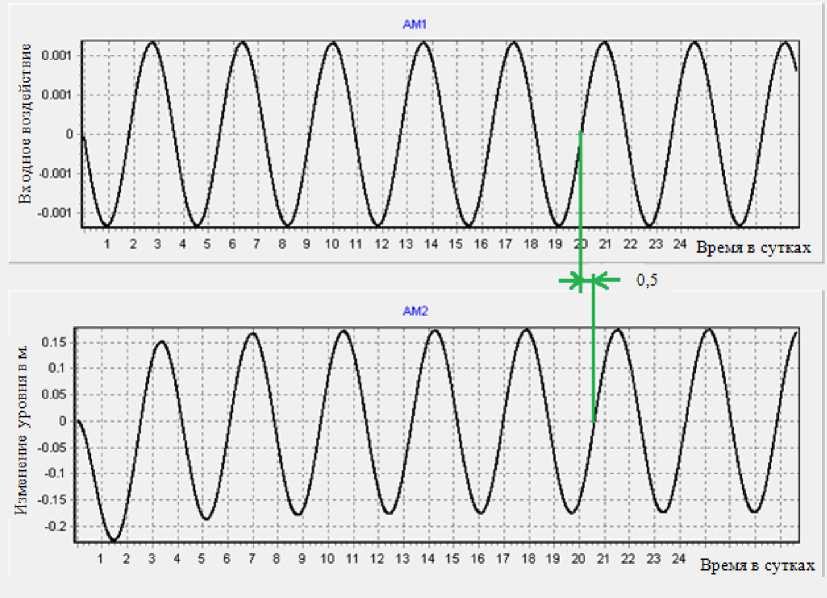
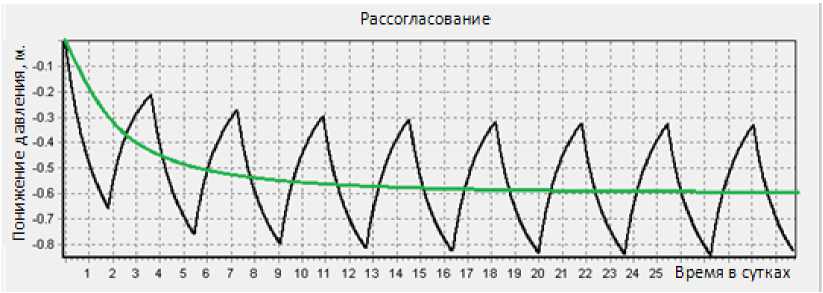
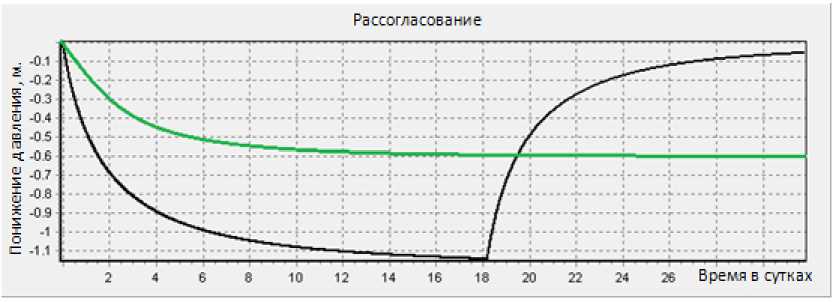
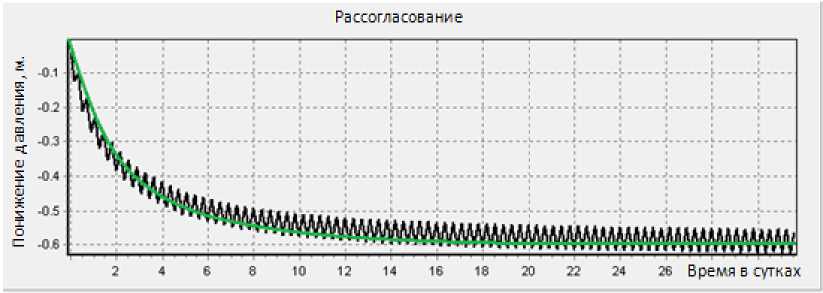
Н2 (х ,0, z, т ) = Н2 (х, Ly, z, т ) = Н2,0, где: h1,0=z (0 Геометрические границы пластов приведены в таблице 1. Таблица 1 Геометрические данные Lx Ly Lz1 Lz2 350м. 1150м. 140м. 50м. Входным воздействием на объект управления служит дебит добывающей скважины Q(τ) , который связан с функцией V(τ) следующим соотношением. V(τ)=Кv·Q(τ). Верификация математической модели объекта управления. Поскольку имеется рабочая скважина, с использованием которой осуществляют добычу гидроминерального сырья, найдём с её помощью коэффициент передачи пласта. Понижение уровня в установившемся режиме, в области расположения заборной скважины составило 0.6м. Определим коэффициент передачи объекта управления К1, К1=0.6/0.00127314=471.275 Из полученной модели найдём коэффициент усиления скважины. Ку=(0.6/0.5)*0.001=0.0012. На основании полученных результатов построим график переходного процесса (см. рис.2). Рис.2 Реакция объекта на статическое входное воздействие Из полученного графика видно, что все коэффициенты найдены правильно и численная модель отражает процесс протекающий в реальном объекте. Определение параметров аппроксимирующего звена. Определим реакцию объекта на динамическое входное воздействие, для этого зададим входное воздействие в виде: Q(τ)=0.0011574·sin(ω1·τ), ω1=0.00001 . По результатам моделирования построим график, приведенный на рисунке 3. Используя результаты моделирования, определим статический коэффициент передачи объекта управления К1 = (изменение уровня в установившемся режиме)/(входное воздействие) К1 = 0.16/0.001157=138.29. Рис.3 Реакция объекта на динамическое возмущение С использованием динамических характеристик (см. рис.3), определим сдвиг по фазе выходного сигнала относительно входного (период колебаний входного сигнала составляет 3,63сут.) ∆φ1 = -2π∙0,5/3,63 = -0.864 рад. Исследование влияния импульсного воздействия на гидролитос -ферные процессы. Рассмотрим построение системы добычи минеральной воды путём импульсного воздействия на скважину. Для получения дискретной передаточной функции разомкнутой импульсной системы по известной передаточной функции непрерывной части системы воспользуемся следующей формулой: Q=K*sin(w*t); Удвоив дебит скважины (Q), подаём его в виде импульсного. Импульсный режим оказывает существенное влияние на уровень понижения давления внутри водяного горизонта, и величина рассогласования превышает допустимый уровень понижения. На основе полученных данных проведём ряд опытов, чтобы сравнить импульсное воздействие с разной величиной периода. Полученные результаты сравним со стационарным воздействием. Рис. 7 Стационарное и импульсное воздействие w:=0.00002 Рис. 8 Стационарное и импульсное воздействие w:=0.000002 Рис. 9 Стационарное и импульсное воздействие w:=0.0002 Уровень колебаний зависит от величины периода воздействия на систему. Интенсивное воздействие на гидроминеральный пласт в импульсном режиме приведет к постепенному загрязнению минеральных вод, и ликвидация последствий такой эксплуатации потребует огромных затрат и длительных сроков реабилитации. Иными словами, гидролитосферные процессы должны рассматриваться как объекты управления со всеми присущими элементами и связями управляемых объектов.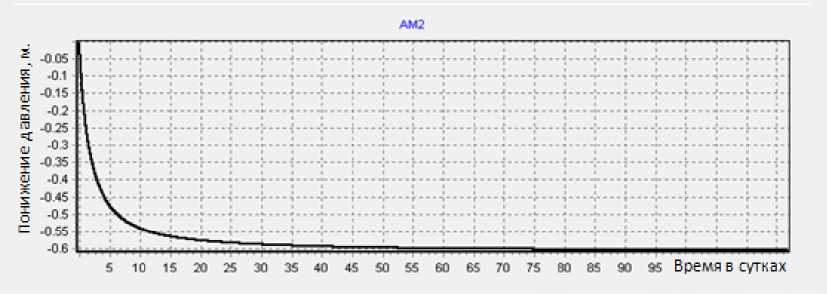
Список литературы Исследование импульсного воздействия на гидролитосферные процессы
- Малков А.В.,Першин И.М., Помеляйко И.С., Першин М.И., Уткин В.А., и др. Кисловодское месторождение углекислых минеральных вод. Системный анализ, диагностика, прогноз и управление. Москва, Наука 2015. 283с.
- Малков А.В., Помеляйко И.С., Першин И.М. Особенности эколого-гидрогеологического мониторинга курортных территорий на примере Кисловодска. Вопросы курортологии, физиотерапии и лечебной физической культуры - научно-практический рецензируемый медицинский журнал. Том 95.Выпуск 2. 2' 2018. С80-82 (140 с.) Web of Science (Russian Science Citation Index - RSCI), PubMed/Medline, Index Medicus, Scopus (через Medline), EBSCOhost, Ulrich's Periodicals Directory, Google Scholar, WorldCat. pp 80-82.
- Дровосекова Т.И., Зверко Е.К. Загрязнения подземных вод на кмв. Форум молодых ученых. 2018. № 4 (20). С. 447-451.
- Дровосекова Т.И. Разработка математических моделей и синтез системы управления гидролитосферными процессами пятигорского месторождения минеральных вод. автореферат дис.. кандидата технических наук / С.-Петерб. гос. электротехн. ун-т (ЛЭТИ). Санкт-Петербург, 2015.
- Дровосекова Т.И., Жерносек И.А. Моделирование гидролитосферных процессов региона кавказских минеральных вод. В мире научных открытий. 2013. № 2 (38). С. 164-176
- Першин И.М., Малков А.В., Першин М.И. Оперативное и стратегическое управление режимами эксплуатации гидролитосферных объектов. Недропользование XXI век. Межотраслевой научно-технический журнал № 6а (44) январь 2014. С. 40-47.


