Исследование информативности признаков при распознавании состояний рельсовых линий

Выделение наиболее информативных признаков – одна из важнейших задач при построении распознающих систем. Размерность признакового пространства зависит от разделяющих свойств признаков: чем информативнее признаки для конкретного образа или класса, тем меньше размерность признакового пространства [1].

Однако до настоящего времени отсутствует формальное решение задачи формирования множества признаков, полностью удовлетворяющее высоким требованиям к распознающим системам в транспорте. Процедура формирования информативного множества признаков иногда затрудняется зашумленностью некоторых наиболее информативных признаков или невозможностью измерить их прямыми методами. Поэтому в неформальных подходах при формировании множества рассматривается несколько путей решения проблемы. Согласно одному из них, информативность признаков для распознавания состояний объектов определяется через исследование качества распознавания, проведенного с использованием выбранных признаков1. Согласно другому, качество признаков определяется исходя из свойств признаков, составляющих образы, без учета распознающих свойств классификатора. Существует два пути формирования множества:

• 1)    с самого начала ведется поиск малого числа признаков с большей информативностью;

• 2)    из большого числа исходных признаков отбираются наиболее полезные для распознавания признаки, и размерность существенно уменьшается.

Ценным свойством описанных подходов является возможность снизить размерность вектора измерений при удачном выборе первичного алфавита признаков [2].

Итак, формально поставленная задача выбора признаков трактуется следующим образом: имеется первичный алфавит признаков X = R^N , на его основе требуется построить рабочее множество признаков Xʹ = Rⁿ размерности n и отображение F:X→Xʹ , обладающие требуемыми свойствами или являющиеся в каком-то смысле оптимальными².

Обозначенная проблема минимизации множества признаков особенно ярко проявляется при построении классификаторов состояний рельсовых линий с множеством информативных признаков и решающих функций.

Приведем наиболее распространенную в настоящее время классификацию рельсовых состояний3:

• -    I класс (нормальный режим) соответствует свободному и исправному состоянию рельсовых линий участка контроля;

• -    II класс (шунтовой режим) соответствует занятому поездом состоянию рельсовых линий участка контроля;

• -    III класс (контрольный режим) соответствует свободному, но неисправному состоянию рельсовых линий участка контроля.

Для построения эффективной системы распознавания состояний рельсовых линий образы, описывающие каждый класс в любой момент времени, должны быть схожими между собой и иметь достаточно близкие значения, но из-за воздействия внешних факторов значения некоторых признаков в образах различных классов могут быть почти идентичными [3–4]. Поэтому предпочтительными будут признаки, индивидуально сгруппированные для каждого класса образов. Другими словами, признаки i- го класса должны существенно отличаться от признаков j- и к- го классов, а этого при классификации состояний рельсовых линий возможно добиться увеличением размерностей алфавита первичных признаков.

Важнейшей особенностью при разработке распознающего устройства состояний рельсовых линий является то, что значения измеренных признаков, составляющих вектор или образ состояний Xj = x 1 , x 2 ,..., x неизбежно подвержены влиянию изменений первичных параметров рельсовых линий вследствие механических и электромагнитных воздействий. Данные воздействия искажают информацию признаков, и это сказывается на всех стадиях процесса, от формирования результатов измеренных значений до классификации состояний решающими функциями d_i = ( x ₁₁, x ₁₂, ..., x_ij , ..., x_pn )^4‒5[5].

Поэтому при формировании множества необходимо учесть особенность различной реакции первичных информативных признаков на внешние воздействия, а при синтезе классификатора состояний рельсовых линий - в первую очередь определить оптимальный набор признаков, квазиинвариантных к внешним воздействиям и обеспечивающих максимальное качество распознавания.

Целью работы является разработка методики анализа информативности признаков на содержательном уровне без учета системы распознавания, а также с учетом обученной системы распознавания с решающими функциями и рекомендациями по формированию рабочего множества признаков.

Обзор литературы

Одной из основных задач при формировании рабочего множества признаков является преобразование первичной информации для удобства кластеризации. В результате такого преобразования расстояния между образами (кластерами) максимизируются, а между значениями признаков внутри классов – минимизируются, т. е. образы становятся более компактными и обладающими более четкими границами классов [6]. При этом, как правило, стремятся также уменьшить размерность пространства признаков, исключая межклассовые признаки, не несущие полезной информации для классификации [7]. В интуитивном понимании образы одного класса должны быть идентичны или иметь практически одинаковые значения ряда признаков. Однако при этом могут присутствовать признаки, довольно сильно отличающиеся внутри образов и по-разному характеризующие различные классы образов.

Для количественных признаков характерна погрешность измерения, поэтому признакам присваиваются коэффициенты, максимизирующие средние расстояния между образами различных классов и минимизирующие расстоя-

Том 28, № 2. 2018 ния между образами одного и того же класса [8]. При статистической и вероятностной оценке информативности и кластеризации интересны методики, раскрытые в работах [9-10], суть которых заключается в оценке плотности распределения. Находятся пики плотности, которые принимаются за центры кластеров или образов, и вокруг данных пиков группируются остальные признаки. Представляет определенный интерес статья [11], где рассматривается адаптивный алгоритм формирования признаков, полученный за счет развития теории распознавания информации на основе модифицированного метода Хаусдорфа путем коррекции координат шаблонов подсистемы формирования образов (кластеров).

Вместе с тем, несмотря на множество методик и алгоритмов группировки признаков, а также способов первичного преобразования исходных данных, при решении практических задач распознавания классов, не допускающих ошибки распознавания, их применимость ограничена, поскольку для построения системы классификации или обучения классификаторов требуются огромные массивы данных.

Решение задачи оценки информативности признаков должно включать также ранжировку признаков. Если признаки независимые, то вычисляя ошибку распознавания для группы N признаков, включающей i -ый признак, а затем для группы без этого признака и сравнивая полученные вероятности ошибок, можно определить, следует ли использовать данный признак. После подобного определения информативности каждого признака выбираются признаки с большей информативностью.

Если признаки зависимые, то процесс ранжировки признаков выполняется по следующему алгоритму:

• 1)    все N признаков исключаются поочередно, как в процедуре, описанной выше;

• 2)    в оставшемся пространстве ( N –1) признаков исследуется критерий качества распознавания;

• 3)    исключается признак, отсутствие которого оказывает наименьшее влияние на величину критерия;

• 4)    в результате поочередного исследования остальных ( N –1) признаков исключается следующий признак;

• 5)    процесс ранжировки повторяется ( N –1) раз.

В качестве меры информативности в алгоритме могут использоваться системные энтропийные меры оценки информативности признаков распознава-ния6 [12–13]. Признаки, уменьшающие неопределенность заданной ситуации, считаются более информативными, чем признаки, которые приводят к увеличению неопределенности распознавания или никак на нее не влияют. Поэтому энтропию можно считать мерой неопределенности, и предпочтительным правилом является выбор признаков, обеспечивающих минимум энтропии границ рассматриваемых классов [14].

Для решения вопросов пренебрежения некоторыми признаками из множества (отнесенными к помехам) предложен ряд способов «элиминирования» признаков.

Согласно [15-16], селекция признаков осуществляется в результате анализа коэффициента корреляции между значением признака и некоторым порогом класса, заданным ранее. По величине коэффициента корреляции элиминируются второстепенные, незначительные признаки. E. A. Патрик в фундаментальной работе7 предложил 6 способов понижения размерности пространства признаков: рассмотрение локального понижения размерности в подпространствах, составляющих образы некоторого класса, изменение проекции пространств признаков, линейное преобразование и др. Однако из-за большого разнообразия операций преобразования приемы не вписываются в единую формализованную математическую процедуру. А. Г. Ивахненко8 предложил осуществлять упорядочение признаков оценкой дисперсии: чем больше дисперсия признака, тем меньше надежность распознавания, и наоборот, поэтому признаки с малой дисперсией более ценны для распознавания.

В работе И. А. Борисова9 процесс селекции осуществляется по следующему алгоритму:

• 1)    формируются классы;

• 2)    на основе экспертного анализа составляется первоначальное множество признаков;

• 3)    оцениваются ошибки классификации;

• 4)    из признакового пространства исключаются поочередно признаки и по величине ошибки формируется рабочее множество признаков.

В статье [17] рассмотрено преобразование признаков путем бинаризации по порогу. Величина порога задается видом самого процесса, и как правило, бинаризация происходит при алгоритме аддитивного выбора порога. Например, в качестве алгоритма предлагается выбор математического ожидания или моды, а также наибольшего пика гистограммы признака.

Результаты анализа научных источников свидетельствуют о недостаточной проработанности вопросов в об- ласти исследования информативности первичных признаков и формирования множества образов, не допускающих пересечения классов; в области исследования информативных признаков при распознавании состояний рельсовых линий исследования практически отсутствуют.

Материалы и методы

В современных системах распознавания состояния рельсовых линий классифицируются по информации одного признака, уровню напряжения на выходе рельсового четырехполюсника или уровню тока на его входе. Поскольку системы классификации состояний рельсовых линий функционируют в условиях воздействия значительных динамических нагрузок и индустриальных помех, классификация по значению одного признака приводит к ошибкам распознавания. Неисправное состояние (например, лопнувший рельс) из-за высокой проводимости изоляции рельсовых линий приводит к ложной классификации, т. е. возможно определение состояния рельсовой линии как исправного и свободного при фактически неисправном [18]. Поэтому прежде чем приступить к построению решающей функции классификатора, необходимо значительно расширить множество признаков для распознавания состояний рельсовых линий, но при этом решить задачу выделения наиболее информативных признаков, инвариантных к воздействию возмущений.

Существует два основных метода к оценке информативности (полезности) признаков, приемлемых для синтеза классификаторов состояний рельсовых линий10. В одном из них выбор признаков осуществляется безотносительно к тому где и как эти признаки в даль-

Том 28, № 2. 2018

нейшем будут использоваться, т. е. вне системы распознавания. Другой метод предполагает оценку информативности с участием системы распознавания, т. е. обучение классификатора осуществляется с использованием набора признаков, после чего с помощью определенного критерия оценивается информативность каждого из этих признаков.

Данные подходы не противоречат, а дополняют друг друга, поскольку на первом этапе считается, что принадлежность признаков к классам неизвестна, и селекция признаков для формирования множества осуществляется по степени их идентичности или взаимосвязи, т. е. происходит элиминирование (первичная обработка) признаков, которые затем, на втором этапе, могут использоваться при распознавании. Для этого применяется обучающая выборка образов, составленная из прошедших селекцию признаков. Данный подход практикуется в сложных, многоуровневых системах распознавания.

Поскольку признаки, вошедшие в текущие образы состояний, могут иметь различную физическую природу и диапазоны изменений (например, при распознавании состояний рельсовых линий используются амплитуды напряжений и токов, фазы токов и напряжений с различными диапазонами изменений), то в целях удобства работы с решающими функциями значения признаков необходимо нормировать, т. е. выразить через безразмерные величины по формуле11:

л i = xj , (1) xi где х/ - нормированное i-ый признак; xi – среднее значение признака.

При реализации первого метода оценки информативности (полезности) признаков в качестве меры использованы корреляционные функции¹² [15; 19], которые позволяют установить взаимосвязь пар признаков x i и x_2i из множества X = { x 1 , x 2 ,..., x n } С этой целью необходимо рассмотре ^. ть попарную комбинацию признаков в каждой строке матрицы (2), составленную из значений признаков путем моделирования или измерения:

X =	x 11 , x 21 ,	x 12 ,. x 22 ,.	..,    x 1 n ..,    x 2 n	.      (2)
	x m 1 ,	xm 2 ,.	..,   xmn

Сочетания пар признаков представлены на рис. 1.

Коэффициентом корреляции двух рассмотренных последовательностей является величина13:

• Г^ = -^— Т ( x i - ^Х 1 )( x 2 i - ^X2 ) , (3)

• ^{1    2} n\°4 i = 1

n

° =      E ( x ^{- x} ) ,       (4)

• У n ¹ i = 1

где n - количество признаков в рассматриваемой последовательности; □ - среднее квадратичное отклонение; x – среднее значение признаков.

Значение r j ~ 1 указывает на однозначную детерминированную зависимость между рассматриваемыми признаками, причем один из признаков не несет информации о распознаваемом образе. Другими словами, данный признак является лишним во множестве, а при

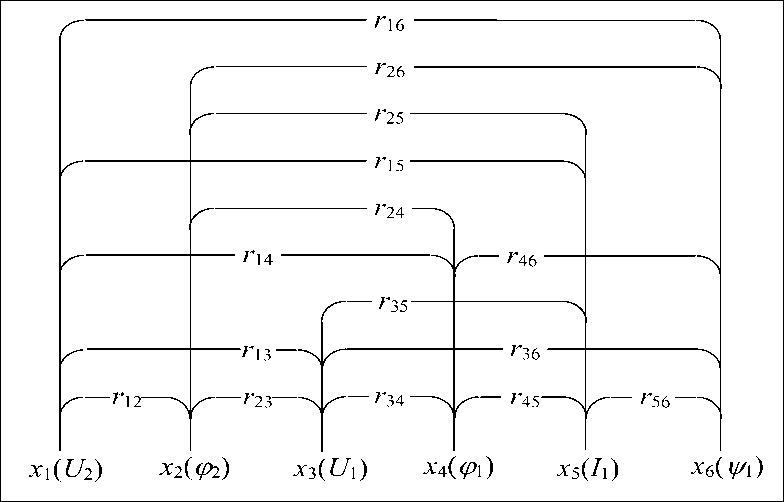
Р и с. 1. Комбинация попарного сочетания признаков F i g. 1. Combination of pairwise conjunction of signs

r < 1 указывает на отсутствие зависимости между признаками, и пара признаков включается во множество¹⁴. При этом в последовательностях { X i }

Том 28, № 2. 2018

и { x 2 } не исключаются повторяющиеся значения.

На рис. 2. представлена блок-схема машинной программы исследования се-

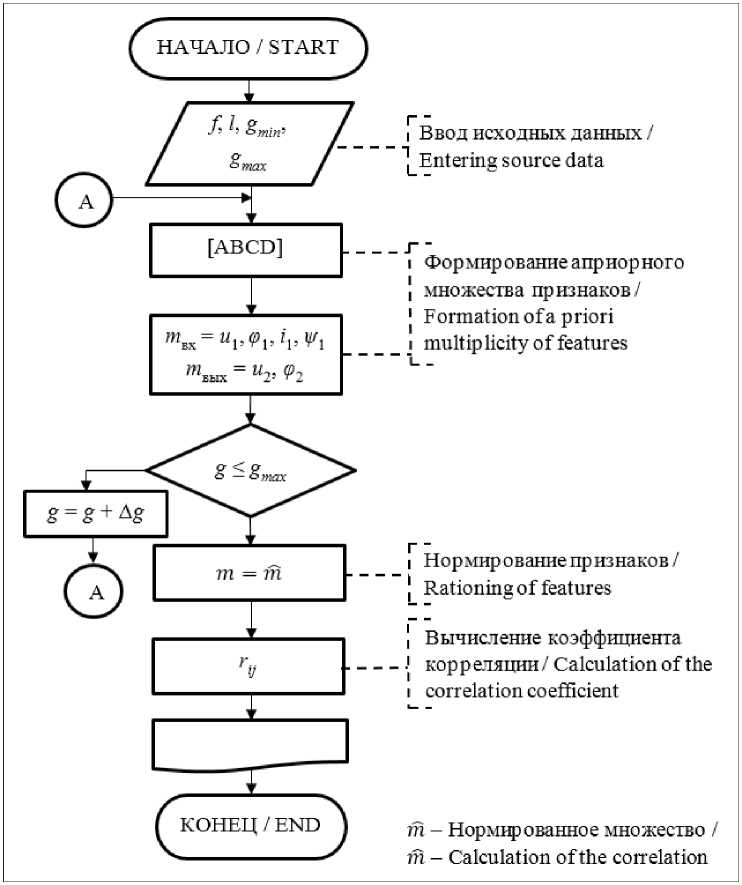
Р и с. 2. Алгоритм исследования корреляционной связи информативных признаков

F i g. 2. The algorithm of the correlation of informative features research лекции, реализованная в среде MATLAB и состоящая из следующих последовательностей:

‒ определение коэффициентов [ А ] матрицы рельсового четырехполюсника;

‒ формирование информационной матрицы ( Х ) первичных признаков;

‒ нормирование коэффициентов матрицы;

• - вычисление коэффициента взаимной корреляции.

Второй метод формирования множества признаков, как указывалось выше, предлагает осуществлять оценку информативности с помощью решающих функций и процедуры обучения15. Для этого выбирается минимальное количество признаков n = 2, вид решающей функции, ее сложность (для практической цели - полином второй степени), производится обучение решающей функции, после чего осуществляется оценка качества распознавания. Затем меняется один из используемых признаков, и процедура повторяется. Если качество распознавания с использованием первой пары признаков выше, чем со второй, то первая пара включается во множество, а процедура повторяется до тех пор, пока не произойдет перебор всего первичного алфавита признаков.

Покажем эффективность подхода с использованием первичного алфавита признаков, состоящего из комплексных амплитуд токов и напряжений на входе и выходе рельсового четырехполюсника. Необходимо учесть, что комплексные амплитуды выходного тока исключаются из рассмотрения, поскольку четырехполюсник рельсовой линии нагружен на входной импеданс классификатора, имеющий постоянную величину, поэтому характер изменения комплексной амплитуды напряжения и тока на выходе рель- сового четырехполюсника совпадает [20–21].

В качестве решающей функции во втором методе использовался полином Колмогорова-Габора, который в общем случае имеет вид16:

n

d (X ) = Cо + ^ Cxa г =1

nn     nnn

+ 22 C j xx, + 222 с ²²² +- (5)

i = 1 j = 1                   i = 1 j = 1 k = 1

где C 0 , C i , C ij , C_ijk - коэффициенты полинома; x_i , x_j , x_k – информативные признаки.

Количество парных сочетаний из обозначенных шести признаков X = {U 1 , Ф 1 ,1 1 , ^ 1 , U ₂, Ф ₂} равно:

TV! 6!

CN = *^=^ = 15 (6)

Следовательно, на основании (5) и рис. 3, а также с учетом x ₁→ U ₂, x 2 ^ ф 2 , x 3 ^ U 1 , x 4 ^ ф 1 , x ₅^ 1 1 , x ₆^ v 1 решающие функции при всех сочетаниях имеют вид:

^f1 ( ^U 2 , ^ф 2 ) = ^C 0 ⁺ CU 2 ^{+ C} 2 ^ф 2 ^{+ C} 3 U 2 ^ф 2 ⁺ + C 4 U 2 + C 5 ф 2 + C 6 U 2 ф 2 + C 7 U 2 ф 2 + C 8 U 2 ф 2 ;

f 2 (U2, U1) = C0 + C1U2 + C2U1 + C3U2U1 + +c4 и22 + c5u1 + c6 и 2 и1 + c7 и 2 и2 + c8 и2u£ f 3 (U2 , ф1 ) = C0 + C1U2 + C2ф1 + C3U2ф1 +

+ C 4 U ₂ ² + C 5 ф 1 + C 6 U 2 Ф 1 + C 7 U ₂ ф 1 + C 8 U 2 ^ ²;

^f 4 ( ^U2 , I 1 ) = ^C 0 ^{+ C}1^U2 ^{+ C} 2 I 1 ^{+ C} 3 U 2 I 1 ⁺

+ C 4 U 2 + C 5 1 ² + C 6 U 2 1 1 + C 7 U 2 1 ² + C 8 U 2 1 1 ;

f 5 ( U 2 , _V 1 ) = C 0 + C 1 U 2 + C 2 ^ 1 + C 3 U 2 ^ 1 + + c 4 и 2 + c _s v 2 + c 6 u 2 v 1 + c 7 и 2 v 1 + c 8 и^

^f6 ^(ф 2 , U 1 ) = C 0 + C 1 ^ф 2 + C 2 U 1 + C 3 ^ф 2 U 1 + + C 4 ^ 2 + C 5 U 2 + C 6 ^ \ u 1 + C 7 ^ 2 и 1³ + C 8 _Ф 22 u 1² ;

f l ( Ф 2 , Ф 1 ) = C 0 ⁺ C 1 ^ф 2 ⁺ C 2 Ф 1 ⁺ C 3 Ф 2 Ф 1 ^{+ +} C 4 ^Ф 2 ⁺ C 5 ^Ф 1 ⁺ C 6 ^Ф 2 ^Ф 1 ⁺ C 7 ^Ф 2 ^Ф 1 ⁺ C 8 ^Ф 2 ^Ф 1² ;

f 8 ( ^ф 2 , 1 2 ) = С 0 + С 1 ^ф 2 + C 2 1 1 + C 3 Ф 2 1 1 + + с 4 Ф 2² + с 5 1 1 + с 6 Ф 2² 1 1 + с 7 ф 2 1 1 + с ₈ ф 2 1 1² ;

^f9 ^(ф 2 , V 1 ) = C 0 ⁺ C 1 ^ф 2 ⁺ C 2 ^ф 1 ⁺ C 3 ^ф 2 ^ф 1 ⁺

⁺ C 4 ^ф 2 ⁺ C 5 V 1 ⁺ C 6 ^ф 2 V 1 ⁺ C 7 ^ф 2 ^ф 1 ⁺ C 8 ^ф 2 V 1 ;

^f i0 ^{( U} 1 , ^ф 1 ) = ^C 0 ⁺ C 1 U 1 ⁺ C 2 ^ф 1 ⁺ C 3 U 1 ^ф 1 ⁺ + C 4 U 1² + C 5 Ф 1² + C 6 U 2 Ф 1 + C 7 Uф + C 8 U 1² Ф 1² ;

^f .1 ( ^U 1 , 1 1 ) = ^C 0 ⁺ C 1 ^U 1 ⁺ C 2 1 1 ⁺ C 3 ^U 1 1 1 ⁺ + C 4 U 1 + C 5 1 1 + C 6 U 1 1 1 + C 7 U 1 1 1 + C 8 U 1 1 1 ;

^f 12 ^{( U} 1 , V 1 ) = C 0 ⁺ CU 1 ⁺ C 2 ^ф 1 ⁺ C 3 ^U1 V 1 ⁺

+ C 4 U ² + C₅ф + C 6 U 2 _V 1 + C 7 Uф + C 8 Uф ;

f i3 ( ^ф 1 , 1 1 ) = C 0 + C ^ф 1 + C 2 1 1 + C 3 ^ф 1 1 1 +

+ C 4 Ф ² + C 5 1 1² + C 6 Ф 1² 1 1 + C 7 ф 1 1 1² + C 8 Ф 1² 1 1² ;

^f i4 ( ^ф 1 , V 1 ) = ^C 0 ⁺ C 1 ^ф 1 ⁺ C 2 V 1 ⁺ C 3 ^ф 1 ^ф 1 ⁺

⁺ C 4 ^ф 1 ⁺ C 5 ^ф 1 ⁺ C 6 ^ф 1 V 1 ⁺ C 7 ^ф 1 Ф 1 ⁺ C 8 ^ф 1 V 1 ;

f i5 ( 1 1 , V i ) = ^C 0 ⁺ C i 1 1 ⁺ C 2 V 1 ⁺ C 3 1 1 V 1 ⁺

+ C 4 1 i² + C₅v i + C 6 1 2 V 1 + C 7 1 i v i + C 8 1 i v i .

Количественная оценка качества распознавания, а следовательно, информативность участвующей пары признаков, составляющих образы состояний по второму методу, включающему в анализ систему распознава-

ния, осуществляется с использованием функции качества разделения клас-сов17–18 [3]:

inf d ( X j ,x₂

NS supd ( X j ,x ₂

■ ,x n ) N

',x n ) S

Pn >  Ps

V ( x,x 2 ,...,x_n ) ,

где K_NS – критерий распознавания I и II классов; inf d ( x 1 ,x 2 ,...,x_n ) N - минимальное пороговое значение решающей функции I класса; sup d ( x 1 ,x 2 ,...,x_n ) ^ - максимальное пороговое значение решающей функции II класса.

K_s = = SK

inf d ( x 1 ,x 2 , supd ( x 1 ,x₂,.

n

S

K

P S >  Pk

V ( x 1 ,x₂ ,...,x_n ) ,

где K_SK – критерий распознавания II и III классов; inf d ( x 1 ,x 2 ,...,x n ) ₅ - мини-

...,

–

мальное пороговое значение решающей функции II класса; sup d ( x 1 , x 1 ,...,x n ) K -

максимальное пороговое значение решающей функции III класса.

Результаты исследования

С помощью Mathcad были прове-

дены исследования взаимокорреляци-онных коэффициентов пар признаков. При моделировании и исследовании были приняты следующие допущения: длина рельсовой линии – 2 км, частота

сигнального тока опроса рельсовых линий – 25 Гц. Результаты исследований представлены на рис. 3.

Из рис. 3 следует, что взаимокор-реляционный коэффициент пар признаков r ₁₂ ( U ₂ и φ ₂) имеет наименьшую величину, равную 0,42, поэтому данная пара считается наиболее информативной, и при создании системы распоз-

• ¹⁷    Тарасов Е. М. Инвариантные классификаторы состояний рельсовых линий для систем интервального управления движением поездов : автореф. дис. … д-ра техн. наук. Самара, 2004. 32 с. URL: http://www.dissercat.com/content/invariantnye-klassifikatory-sostoyanii-relsovykh-linii-dlya-sistem-intervalnogo-upravleniya-

• ¹⁸    Ивахненко А. Г. Самообучающиеся системы распознавания и автоматического управления. Киев : Техника, 1969. 392 с. URL:

навания рационально использовать сочетание признаков U ₂ и φ ₂. Следующей парой признаков, имеющей наименьший коэффициент корреляции, является фаза тока на входе и напряжения на выходе рельсовой линии, у которой значение взаимокорреляционного коэффициента равно 0,48. При синтезе более сложной решающей функции с тремя признаками – аргументами, следовательно, необходимо использовать амплитуды и фазы напряжения на выходе рельсовой линии, а также фазы тока на ее входе. Остальные сочетания, как видно на рис. 3, имеют высокий коэффициент корреляции ≈ 1, поэтому их следует исключить из множества.

Рассмотренный подход осуществляет классификацию на первичном, признаковом уровне. Более сложные системы и алгоритмы распознавания предполагают использование решающих функций и обучение классификатора.

При исследовании информативности вторым методом с использованием решающих функций, согласно (7), попарное сочетание признаков имеет вид:

d i = f(U 2 ф ) d 2 = f(U , U ₂ ); d 3 = f(U 2 , ф ); '

d 4 = f (U 2 , ^ ); d 5 = f (U 2 ,I i ); d 6 = f ( ф ,U i );

d 7 = f ( ф , ф ); d 8 = f ( ф 2 ,I i ); d 9 = f ( Ф 2 , ^ i ); - .

d io = f (U , , ф ); d u = f (U , ,I i ); d i2 = f ( U i , ^ i );

d i3 = f ( ф ,1 1 ); d i4 = f ( ф^ ); d i5 = f ( I i , ^ i ).

Решающее правило при оценке информативности по второму методу звучит следующим образом: те сочетания признаков, при использовании которых решающая функция имеет максимальное значение критериев качества распознавания, являются наиболее информативными.

На рис. 4. представлены результаты анализа качества распознавания классов двумерными образами с использованием полинома Колмогорова-Граба-ра в качестве решающей функции.

Согласно требованиям обеспечения безопасности движения поездов,

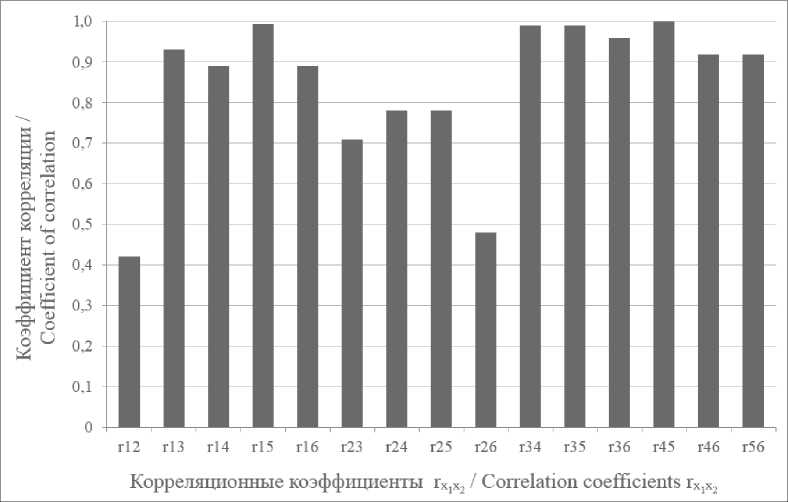
Р и с. 3. Значения взаимокорреляционного коэффициента

F i g. 3. Values of the correlation coefficient

2.0

^

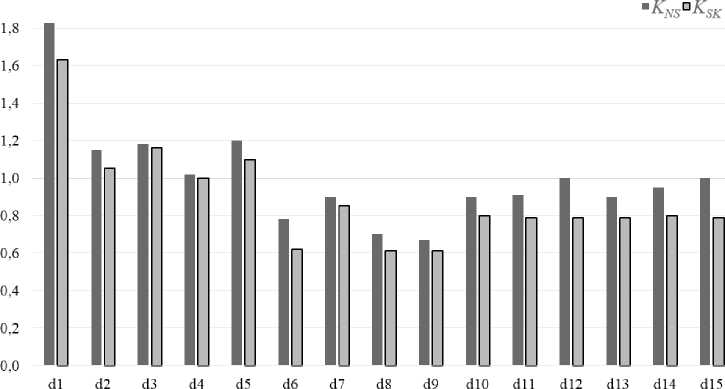
Решающие функции d(X) / Decisive functions d(X)

Р и с. 4. Значения функций качества разделения двумерными образами F i g. 4. Values of separation quality functions by two-dimensional images

критерий разделения классов должен иметь значения КNS и КSK ≥ 1,1–1,2, т. е. границы классов должны быть четкими, и классы никогда не должны пересекаться. И сочетания признаков, используемые в решающей функции обученного классификатора и позволяющие правильно распознавать классы, обладают характерными свойствами и наиболее информативны. Такими сочетаниями при распознавании I и II классов, согласно рис. 4, являются d1 (КNS = 1,8638; КSK = 1,4799) и d3 (КNS = 1,1637; КSK = 1,1170). Данные сочетания обеспечивают инвариантность к возмущающим воздействиям, поскольку диапазон изменения проводимости изоляции рельсовых линий, принятый при моделировании, составляет от 4 до 0,02 см/км, что в 4 раза больше нормативного, принятого при проектировании классификаторов. Во всех парах признаков присутствует амплитуда напряжения на выходе рельсовой линии, и это указывает на ее наибольшую информативность. Также во множество предпочтительно включить амплитуду и фазу напряжения на входе рельсовой линии и фазу на ее выходе.

При распознавании II и III классов наиболее информативны сочетания признаков, входящие в решающие функции d ₁₀– d ₁₅ которые обладают приемлемым качеств^, ом распознавания. Это связано с зависимостью фазы тока на входе рельсовой линии от неисправности рельсовой линии: d ₁₀ ( К_SK = 0,9145 при К_NS = 0,6575), d ₁₁ ( К_SK = 0,9438 при К_NS = 0,6125), d 12 ( K SK = 0,9815 при K NS = 0,5584), d 13 ( К SK = 0,9214 при К NS = 0,6203), d ₁₄ ( К_SK = 0,9615 при К_NS = 0,6184), d ₁₅ ( К_SK = 0,9807 при К_NS = 0,5825).

Путем оптимизации значений элементов устройств согласования аппаратуры классификатора с рельсовой линией в начале и в конце участка контроля можно добиться увеличения значений критериев К_NS и К_SK до ≥ 1,2, что благоприятно скажется на обеспечении безопасности движения поездов.

Обсуждение и заключения

Одной из важнейших задач при распознавании состояний различных объектов является формирование ра- бочего алфавита признаков, имеющего меньшую размерность, чем априорный словарь признаков. Это позволяет уменьшить экономические потери при создании сложной системы распознавания, минимизировать ошибки при измерении множества признаков, уменьшить время обработки информации, которое особенно важно при распознавании состояний рельсовых линий в реальном времени. Данная проблема особенно актуальна при распознавании состояний рельсовых линий с распределенными параметрами, поскольку объект распознавания находится под непрерывным воздействием механических, электромагнитных и климатических воздействий, оказывающих существенное влияние на измеряемые первичные признаки. Более того, системы распознавания распределены вдоль железнодорожных путей, решающие устройства реализованы на промышленных микропроцессорах, которые должны обеспечить процесс распознавания в реальном времени, и от размерности множества первичных информативных признаков зависит время обработки информации и классификации состояний рельсовых линий. В работе рассмотрены два под- хода к оценке информативности признаков: с участием обученной решающей функции и вне системы распознавания на первичном уровне. Сравнение результатов исследований корреляционными функциями и обученными решающими функциями подтверждает гипотезу о том, что подходы не противоречат друг другу: как в первом, так и во втором случае наиболее информативны амплитуды и фазы напряжений на выходе рельсовой линии, а также амплитуд напряжений на ее входе (ru,φ→ min; КNS, КSK→ max).

Результаты, полученные в ходе исследования информативности признаков для распознавания состояний рельсовых линий корреляционным анализом и с использованием решающей функции классификатора, подтверждают возможности подходов при формировании рабочего множества признаков и могут быть использованы при разработке обучаемых классификаторов состояний.

Сочетание двух методов позволяет синтезировать сложные, многоуровневые системы распознавания, что является основным вкладом данной работы в развитие принципов распознавания образов.

Поступила 29.01.2018; принята к публикации 26.03.2018; опубликована онлайн 29.06.2018

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.