Исследование интегрального уравнения Салема
Автор: Давлатов Ш.О.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Основной раздел
Статья в выпуске: 5 (119), 2025 года.
Бесплатный доступ
В этой статье построена абстрактная интегрируемая функция. Показано, что она не является нетривиальным решением интегрального уравнения Салема.
Абстрактная функция, уравнения салема, нетривиальное решение, гипотеза римана
Короткий адрес: https://sciup.org/140311707
IDR: 140311707
Текст научной статьи Исследование интегрального уравнения Салема
Рассмотрим следующую функцию
VW =
1 при иррациональных z g\0,1\, О при рациональных z е [0,1].
Функцию ^(-) запишем виде суммы двух функций ^(^) = ^i(^) + ^2(z)
На отрезке [0,1] функция У^) имеет два значения ноль и единица. На этом отрезке при переходе слева направо каждого рационального числа значение функции ^i(z) изменяется, то есть значения функции чередуются. На этом отрезке первым значением функции ^i(^) является единица. Точно также на отрезке [0,1] функция ^2G0 имеет два значения ноль и единица. Значение функции ^2 GO изменяется при переходе слева направо каждого рационального числа, то есть значения функции ^2(з) чередуются. Первым значением функции ^2 GO является ноль. Из интегрируемости функции ^(-) следует интегрируемость функций .
Теперь рассмотрим функцию ^) = ^1(^)-^2(Z). Очевидно, что функция ^U) имеет два значения 1 и -1 на отрезке [0,1] . На этом отрезке, значение функции ^(^) изменяется при переходе слева направо каждого рационального числа, то есть значения функции чередуются. Ясно, что на этом отрезке первым значением функции ^(-) является единица. Очевидно, что функция ^(^) интегрируема, так как функции ^iGO’^GO интегрируемы.
Ясно, что
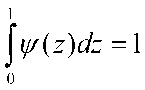
Возникает вопрос чему равен следующий интеграл?
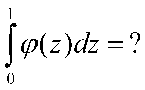
Если количество рациональных чисел на отрезки [CM] нечетное, то
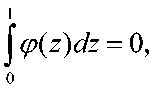
а если четное, то
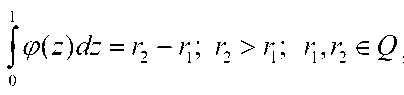
где Z1 ’ Г2 соседние рациональные числа, Q - множество рациональных чисел.
Теорема. Гипотеза Римана истинна тогда и только тогда, когда интегральное уравнение или функция от x
e i среди ограниченных и измеримых функций имеет только тривиальное решение J (y) для 0 В интеграле (1) сделаем замену переменных . После замены интеграл (1) имеет вид: Рассмотрим последовательность функций вида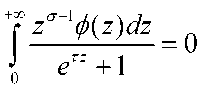
|
Ж) = < |
(-1)' при ze 1 + —,1+^2L4 / = 0...77-1, \ n n / 0 при остальных значениях z. |
и
Вычислим следующий интеграл где
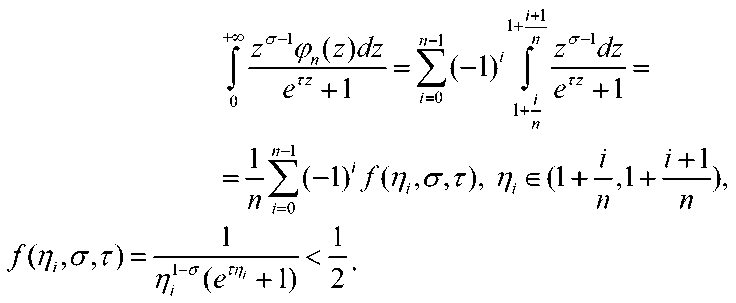
Очевидно, что
/(По , сг, г) > /(771 ,а,т)> f(p,,a,T)>...> / (р^ , сг, г) > О
° < Ё*-1)'/^^ И < .Ж^ г)
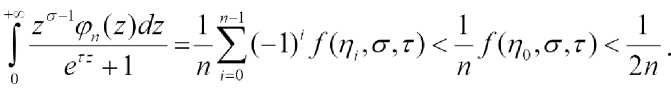
Следовательно
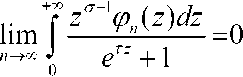
Рассмотрим множества A=U + -, / = О,/? >, 77 = 1,2,3,
.
Q множество
Очевидно, что Л = 2гф,21; иДсО , где рациональных чисел.
функцией ^-1) на является предельной легко, убедится, что
Учитывая это и сравнивая функций чАА с отрезке [1,2], вроде кажется, что функция ^-1) функцией последовательности функций ^A) . Но последовательность функций чАА не сходится не по какому определению сходимости к ^-1) на отрезке [1,2]. Поэтому r z° '^(z - \)dz _ ?
Литературы.
№5(119) 2025


