Исследование интегрального уравнения Салема с помощью последовательности функций
Автор: Давлатов Ш.О.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Основной раздел
Статья в выпуске: 5 (119), 2025 года.
Бесплатный доступ
В этой статье построена последовательность функций. С помощью последовательности функций исследовано интегральное уравнение Салема.
Последовательность функций, уравнения салема, нетривиальное решение, гипотеза римана
Короткий адрес: https://sciup.org/140311706
IDR: 140311706
Текст научной статьи Исследование интегрального уравнения Салема с помощью последовательности функций
|е-7Ш=0 (1
среди ограниченных и измеримых функций имеет только тривиальное решение / (у) для 0<а<1, хе R [1].
В интеграле (1) сделаем замену переменных z = е у ,т = ех; t,z е(0,+сс^
После замены интеграл (1) имеет вид:
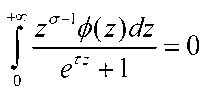
Рассмотрим последовательность функций вида
(-1)' при ze[l+—,1+ — I п п
, 7=0,/7-1
0 при остальных значениях z.
Последовательность функций
Z)
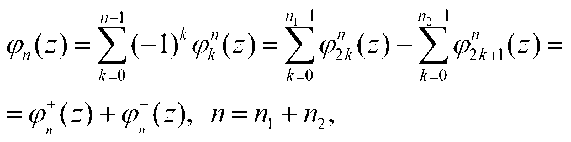
где
(Р'№ = <
л Л к , к + 1} 1 При ZE 1+—,14--,
V п п J
О при остальных значениях z,
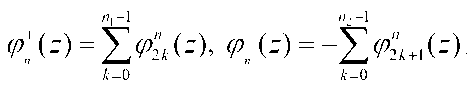
Функции ^(^п^ интегрируемы и
О если се(-со,1]
J P~SZ№ = p[z: z g[1,2]} = [1.2]
% +1
' --- если ce(l,+®)w n нечетный,
n
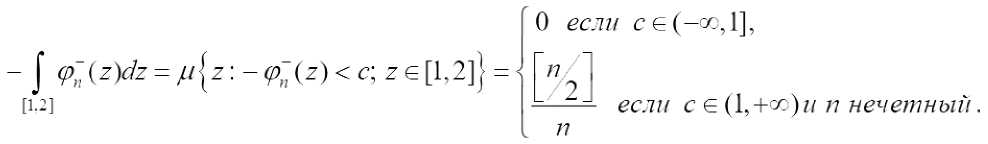
Теорема 2. Если ЛЛ положительная, непрерывная, строго
монотонная функция на [1,2] , то
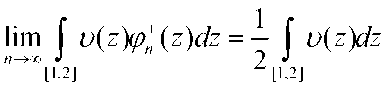
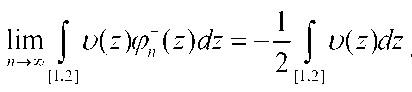
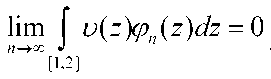
Доказательство. Пусть ^(z) положительная, непрерывная строго убывающая функция.
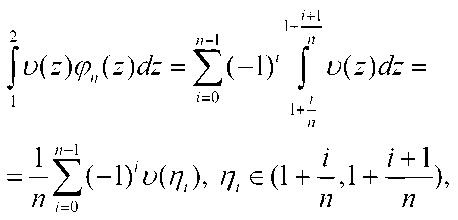
где и^Г!^< К = const по теореме Вейерштрасса. Xz) строго убывающая функция, поэтому
и
/(-1
^<^-^У^<^(11^ , /=0
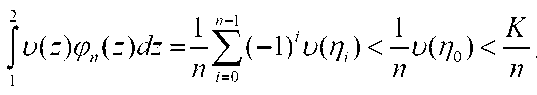
Откуда
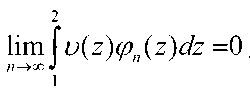
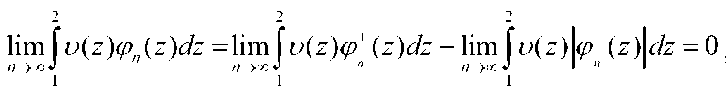
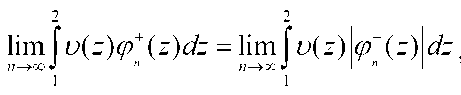
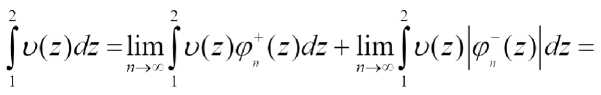
2lim \ v(z)(p+ (z)dz = 21im \ u(z)(p~(z)dz
JI—>00 * ” /7—>00 J”
Следовательно
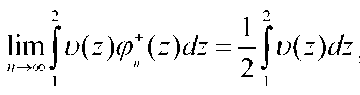
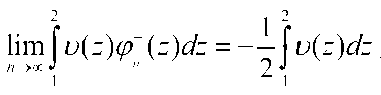
Аналогично доказывается, когда ^{z} строго возрастающая функция
Теорема доказано.
Из теоремы 2 следует, что
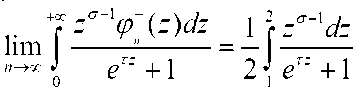
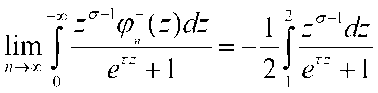
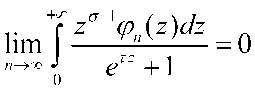
Литературы.
№5(119) 2025


