Исследование интерферометра сдвига в фазоизмерительных приборах и системах расшифровки голографических интерферограмм

Голографическая интерферометрия является высокоинформативным и высокоточным инструментом получения данных. Уникальность методов голографической интерферометрии обусловлена ее возможностями [1]. Эти методы

– позволяют проводить исследования статических и динамических процессов;

– не предъявляют требований к качеству поверхности контролируемых объектов;

– позволяют производить сравнение волновых полей, существовавших в различные моменты времени;

– позволяют получать информацию об исследуемом процессе как в количественном, так и качественном аспектах;

– позволяют воспроизводить трехмерную видеокопию изучаемого объекта.

При исследовании напряженно-деформированного состояния диффузно отражающих объектов используются два подхода. Первый подход заключается в получении голографических топограмм поверхности объекта. Целью второго подхода является получение голографических интерферограмм возмущенного объекта [2].

Методы голографических топограмм в большинстве случаев используются для качественной оценки результатов исследований.

Наиболее информативными и точными являются методы голографической интерферометрии возмущенного объекта. Эти методы используются не только при качественном анализе, но и для количественной интерпретации результатов наблюдений.

Среди методов изучения возмущенного объекта можно выделить метод двух экспозиций. Этот метод достаточно легко реализуется, обеспечивает максимальный контраст интерференционного поля, позволяет одновременно реконструировать объектные волны, существовавшие на различных этапах исследования, а также допускает длительное хранение записанной информации.

Исследования, проводимые с использованием метода двухэкспозиционной голографической интерферометрии, можно разделить на следующие этапы:

– регистрация голографической интерферограммы;

– оптическая обработка полученной интерферограммы;

– анализ полученных данных [3].

Со времени первых шагов голографической интерферометрии по внедрению в научную и лабораторную практику большие успехи достигнуты в методике регистрации интерферограмм. Современный уровень развития вычислительной техники и компьютеризация научных исследований позволяют успешно решать задачи третьего этапа — проводить качественный анализ и количественную интерпретацию полученных экспериментальных данных. Однако нет достаточных оснований утверждать, что решены все проблемы в разработке средств и методов оптической обработки голографических интерферограмм.

Изучение существующих подходов к считыванию информации с голографической интерферограммы показало, что наиболее точными и информативными являются фазоизмерительные гетеродинные системы [4], в которых фазовые характеристики интерференционного поля трансформируется в фазу электрического сигнала. Измерение последней осуществляется с применением электронной аппаратуры. Использование указанного технического решения позволяет в значительной степени снизить погрешность измерений и расширить диапазон определяемых величин.

ПОСТАНОВКА ЗАДАЧИ

Для анализа функционирования системы обработки голографических интерферограмм с применением двухчастотного излучения необходимо конкретизировать вид используемого интерферометра сдвига и получить аналитическое выражение для разности фаз лучей, прошедших интерферометр. Из соображений виброустойчивости, а также простоты конструкции в работе предлагается использовать интерферометр Жамена, образованный двумя идентичными плоскопараллельными пластинами [5–9]. Точность, на которую претендуют данные измерений по методике, предлагаемой в настоящей работе, требует анализа интерферометра в строгом изложении.

Информация о векторе смещения содержится в изменении разности фаз ∆ φ . Метод гетеродинной голографической интерферометрии предполагает преобразование фазы интерференционных полос φ в фазу электрического сигнала Ф, которая измеряется с помощью электронной техники.

Однако сигнал интерферометра формируется в результате интерференции всех присутствующих на выходе интерферометра лучей [6, 12, 13]. Поэтому зависимость Ф от φ носит сложный характер. Для оценки погрешности измерений необходимо выяснить, как влияет наличие составляющих

U И — амплитуды, вносимой интерферометром, и U ∑ — суммарной амплитуды выходного интерференционного сигнала на зависимость Ф( φ ).

Нелинейность зависимости разности фаз выходных лучей интерферометра в пределах апертурного угла наблюдения с необходимостью приводит к деформации интерференционного поля и, как следствие, падению амплитуды выходного сигнала. Поэтому для определения верхней и нижней границ диапазона измерений необходимо рассмотреть график зависимости амплитуды выходного сигнала от угла наклона пластины интерферометра ξ .

ВЛИЯНИЕ ПЕРЕКРЕСТНОЙ ИНТЕРФЕРЕНЦИИ НА ТОЧНОСТЬ ИЗМЕРЕНИЙ

Аналитическое рассмотрение

Итак, фаза интерференционных полос φ в направлении, характеризуемом апертурным углом α = α 0 , изменилась от значения φ = φ 01 до φ = = φ 02 = φ 01 + Δ φ . Соответствующее изменение фазы выходного сигнала — от Ф = Ф 1 до Ф = Ф 2 = Ф 1 + + ΔФ. Изменение фазы выходного сигнала ΔФ обусловлено изменением фазы полос Δ φ . Получим зависимость ΔФ от Δ φ в следующем виде:

ф =

= arctg{[^оИ8т фо + U0Z sin^oz + Uод siwA0 ]x x [U0И cosФио + UoZ cosФо^ + U0Д cosФдо]-1} . (1)

Далее, при настроенном интерферометре можно констатировать явное доминирование изменения амплитуды сигнала U 0Δ над U 0И . Поэтому, воспользовавшись малостью величины χ = U 0И / U 0Δ , разложим выражение для Ф в ряд, пренебрегая членами второго и более высоких порядков малости

Ф = Ф (0) + ^{дф (0)} x .

d x

Функция Ф при χ = 0 принимает следующий вид:

Ф(0) = φ ₀ – φ _0И.

Соответственно для первой производной получим дФ(0)       .        1 . п

—---= - sin Ф о + —^sin2 Ф o .

d x     L 4        _

Тогда

Ф = φ 0 – φ 0И – [sin φ + sin2 φ ].

Принимая во внимание, что

Ф 1 = Ф( φ 0 = φ 01 ); Ф 2 = Ф( φ 0 = φ 02 ); φ 02 = φ 01 + Δ φ ,

запишем

ΔФ = Δφ + δφ, где для ошибки, обусловленной перекрестной интерференцией, имеем следующее выражение:

'

8ф = sin Ф 01 + 4^Sin2 Ф o1 X 1

—

—

sin ( ^ 01 ^{+ А} ф ) + 4sⁱⁿ ( 2 ^ 01 + ^{2 А} ф ) X

Таким образом, выражение (2) оценивает влияние перекрестной интерференции на точность измерений.

Расшифровка голографических интерферограмм по методу Александрова и Бонч-Бруевича

Согласно этому методу [7], три искомых уравнения получаются за счет изменения направления наблюдения k H анализируемой точки поверхности объекта. Вектор смещения d при этом не меняется, и Δ d = 0. Следовательно, (2) принимает следующий вид:

фазы полос происходит за счет изменения вектора смещения при переходе от одной анализируемой точки поверхности объекта к другой. Поэтому, в соответствии с [8, 14, 15],

2 π

Аф = —а Аd , λ где Δd — разность величины смещения между двумя точками поверхности.

Для рассматриваемого режима переход от одной точки поверхности к другой сопровождается расcтройкой интерферометра. Поэтому χ 1 ≠ χ 2 . Если принять, что d 1 — смещение в начальной точке анализа, Δ d — изменение величины смещения, то получим

5ф =

—

5ф =

sin Ф 01 + 4Sin2 ф o1

— sin ( Ф 01 + А ф ) —

sin ф о1 + 4Sin² Ф o1

Sin ( ф 01 ^+А ф )

--Sin

( 2 ф 01 + 2 А ф )

χ ,

где χ = χ 1 = χ 2 .

Наличие в полученном выражении в качестве аргумента функции sin величины Δ φ позволяет сформулировать следующий вывод: если изменение направления наблюдения подчинить условию, что изменение фазы полос будет кратно 2 π , ошибкой δφ , обусловленной перекрестной интерференцией, можно будет пренебречь.

Режим измерения относительного изменения фазы интерференционных полос

Этот режим может быть реализован в случае обработки двухэкспозиционных голограмм сфокусированных изображений, а также в случае, когда голограмма регистрируется в полосах конечной ширины. Для этого режима изменение

ф = arctg <

λ d πα 1Н

+ —Sin

( 2 ф 01 + ^{2 А} ф )

X

2 А d

^{X .}

, . 2Аdna d sin Н                            (5)

1 λ

Выведенные соотношения (3) и (5) снимают вопрос о влиянии перекрестной интерференции при оптической обработке голографических интерферограмм с применением сдвиговой интерферометрии. Возникающая при этом погрешность, во-первых, доступна оценке, во-вторых, является величиной контролируемой и управляемой в зависимости от геометрии схемы наблюдения, шага изменения фазы полос при съеме информации, а также от несущей частоты голографического интерференционного поля.

С целью графической интерпретации сформулированных выводов на рис. 1–4 представлены результаты расчетов фазового отклонения величины ΔФ от истинного значения Δ φ . Расчет фазовой ошибки δφ производился по следующей формуле:

5ф = А ф — [ф 2 ( ф ио , ф о , А ф , А d ) —

— Ф1 ( фио, фо, Аф, А d )], где Δφ — изменение фазы интерференционных полос; Ф — фаза сигнала:

_Sin ^{2 па} н ^d и          _Sin ^{2 na} H ^{( d} и ^{+ d + А d} )                     _Sin ^{2 na} H ^{А d}

-----^ ---^Sin ф ио +----------- ^Sin ( ф ио + ф о + ^А ф )-- ^ ---^{Sin А} ф d и                 d и + d + А d                          А d

X

X

2πα d sin Н И

---^--cos Ф ио ⁺ d _Н

. 2nd _Н ( d И + d + A d )

λ

d И + d + A d

. 2па A d sin ^Н cos ( ф _И0 + ф ₀ + А ф )-- -^---cos А ф

1 -1'

2 πα d       2 πα d

Ф ио = Л^; Ф о = ~~ λ λ

.

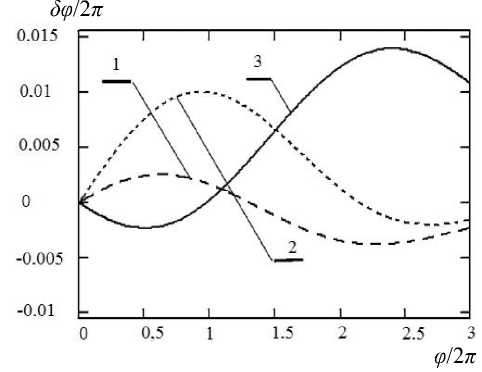
Рис. 1. Фазовая погрешность в режиме расшифровки голографических интерферограмм по методу Александрова и Бонч-Бруевича.

1 — α _Н = 0.1 рад, 2 — α _Н = 0.15 рад, 3 — α _Н = 2 рад

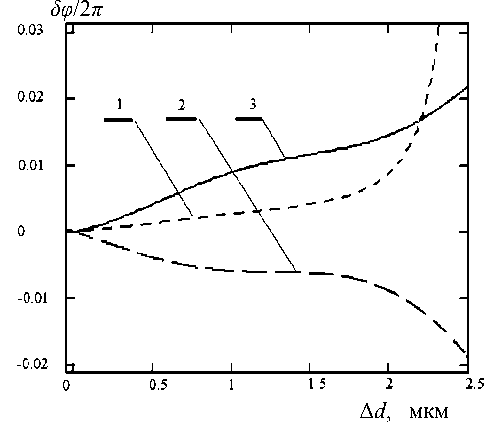
Рис. 2. Фазовая погрешность в режиме измерения относительного изменения фазы интерференционных полос.

1 — α _Н = 0.1 рад, 2 — α _Н = 0.15 рад, 3 — α _Н = 2 рад

Расчеты проводились для рассмотренных выше случаев.

В режиме относительных измерений (рис. 2) d = dИ+ Δd, где Δd — величина смещения, характеризующая расстройку интерферометра;   Аф = —a Ad —

λ изменение фазы полос при сканировании голограммы; Ф1 = Ф(φ0, φ0,0,0), Ф2 = Ф(φ0, φ0, Δφ, Δd).

Расчеты выполнены для различных величин апертуры фотоприемника. Как следует из графических зависимостей, при малой расстройке интерферометра (до ~2 мкм) меньшая фазовая ошибка соответствует большей апертуре фотоприемника, что физически объясняется значительным превышением компоненты U ∆ над U И и U ∑ . Однако по мере увеличения расстройки интерферометра картина меняется на противоположную: бόльшая апертура фотоприемника обусловливает и бόльшую погрешность. Это объясняется тем обстоятельством, что доминирование амплитуды составляющей U ∆ над U И и U ∑ для меньшей апертуры менее критично к расстройке интерферометра. Таким образом, для расстройки, не превышающей 2 мкм, ошибка измерений в режиме определения относительной величины вектора смещения не превышает 0.015 рад, что составляет 0.002 доли интерференционной полосы.

Для случая обработки голографических интерферограмм по методу Александрова и Бонч-Бруевича настройка интерферометра не нарушается, и dИ = d, Δd = 0, Ф1 = Ф(φ0, φ0,0,0), Ф2 = Ф(φ0, φ0, Δφ, 0).

Как видно из графиков (рис. 2), ошибка измерения фазы также не превышает 0.002 полосы.

Зависимость фазовой погрешности от величины измеряемого смещения

Величина смещения d определяет соотношение между амплитудами составляющих U ∆ , U И и U ∑ , что обусловливает величину фазовой погрешности.

δφ /2 π

0.02

20        25        30

Δ d , мкм

Рис. 3. Зависимость фазовой погрешности от величины смещения ( d = 0–30 мкм).

1 — α _Н = 0.1 рад, 2 — α _Н = 0.15 рад, 3 — α _Н = 2 рад

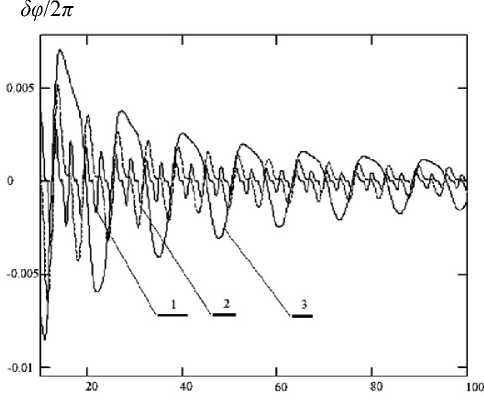
Δ d , мкм

Рис. 4. Зависимость фазовой погрешности от величины смещения ( d = 15–100 мкм).

1 — α _Н = 0.1 рад, 2 — α _Н = 0.15 рад, 3 — α _Н = 2 рад

На рис. 3 представлена графическая интерпретация данного утверждения.

Для небольших величин d превышение U∆ над UИ и U∑ не столь очевидно. Как следствие — относительно большая погрешность измерения (до 0.06 /2π). Однако с ростом d отношение U∆/(UИ, U∑) растет, погрешность падает. Также из графиков на рис. 4 следует, что зависимость δφ от величины смещения d можно сделать сколь угодно малой, придавая объекту между экспозициями дополнительное искусственное смещение. Так, из рис. 4 следует, что при дополнительном смещении ~10 мкм максимальная ошибка не превышает 0.001 доли интерференционной полосы.

УРАВНЕНИЕ ИНТЕРФЕРЕНЦИИ ДЛЯ ИНТЕРФЕРОМЕТРА СДВИГА

Очень важным является вопрос о границах применимости интерферометра. Эта информация может быть получена при строгом анализе разности хода интерферирующих лучей.

Сдвиг в разность фаз, а также в пространственное положение соответственных элементов А и В вносится посредством взаимного наклона пластин интерферометра (рис. 5). Причем угол наклона характеризуется величиной ξ при наклоне пластины II относительно оси Y2 и величиной ζ — при наклоне относительно оси Х 2 . Амплитуда сигнала на выходе интерферометра (при настроенном интерферометре) постоянна и не зависит от величины измеряемого смещения. Однако функция разности хода интерферирующих лучей от координат поля интерференции на выходе интерферометра показывает нелинейность этой зависимости. Следовательно, разность хода лучей, распространяющихся от соответственных элементов, не может быть скомпенсирована разностью хода, вносимой интерферометром для всех точек поля интерференции. Отсюда неизбежное падение амплитуды сигнала при росте величины измеряемого смещения. Кроме того, вектор сдвига, вносимого интерферометром, имеет разную пространственную ориентацию относительно плоскости расположения соответственных элементов (или их изображений) в зависимости от осей наклона пластин интерферометра. Следовательно, нелинейность, создаваемая интерферометром, имеет разную геометрическую зависимость.

С целью графической интерпретации сформулированных выводов имеем выражение следующего вида [9, 15, 16]:

φ И ( α х , α у , ξ , ζ ) = φ 1 ( α х , α у , ξ , ζ ) –

– φ 2 ( α х , α у , ξ , ζ ), (6) где ξ , ζ — углы наклона второй пластины интерферометра вокруг осей Y 2 и Х 1 соответственно; φ 1,2 ( α х , α у , ξ , ζ ) — разность фаз лучей на выходе первой и второй пластин интерферометра соответственно;

^ 2 ( ^a x , ^a y , ^ , ^Z ) =

4 π nh λ

1 -

cos2α tg (ax + Z ) + tg (ay + Z ) ---_ v ' cos (ax + ^)

n 2 tg ² ( ^a x + ^Z ) + tg ² ( ^a y + ^Z )

cos ² α_x

^ 1 ^{( a} x , ^a y , ^Z, ^Z ) = ^ 2 ^{( a} x , ^a y , ^Z, ^Z )| ^ , _z = 0

cos ² ( ^a x + ^Z ) _

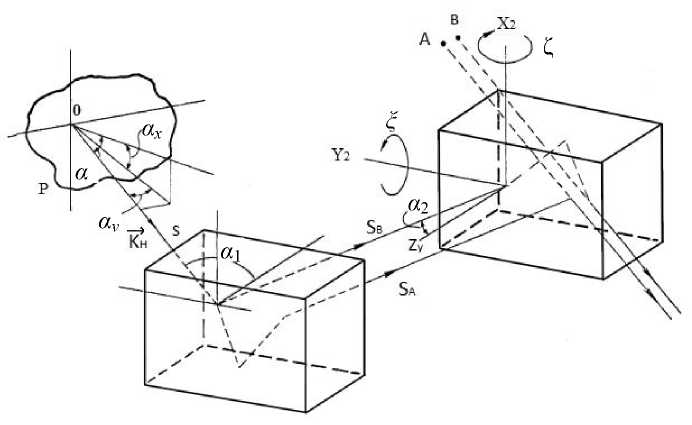
Рис. 5. Геометрия хода лучей в интерферометре Жамена.

P — объект; A, B — соответствующие элементы; X₂, Y₂, Z _y — оси вращения второй пластины интерферометра; S — объектная волна; S A , S B — объектные волны после прохождения первой пластины интерферометра; α — угол наблюдения; α х , α у — соответствующие проекции угла наблюдения; α 1 , α ₂ — углы наблюдения на первой и второй пластинах интерферометра; ξ — наклон второй пластины по оси Y 2 ; ζ — наклон второй пластины по оси Х 2 ; K _Н — волновой вектор, характеризующий направления наблюдения

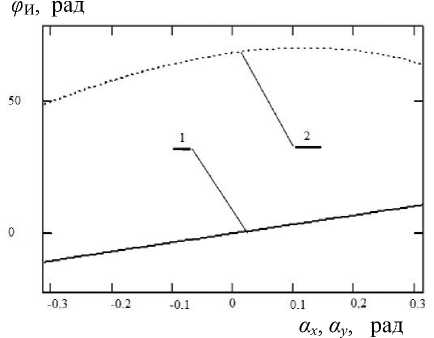
Рис. 6. Изменение фазового сдвига, вносимого интерферометром, по угловой апертуре интерференционного поля при наклоне пластины интерферометра относительно оси Y 2 (1), относительно оси X 2 (2)

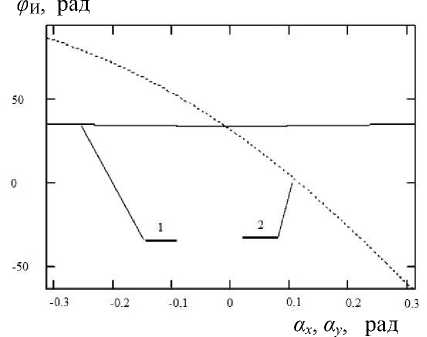
Рис. 7. Изменение производной фазового сдвига, вносимого интерферометром, по угловой апертуре интерференционного поля при наклоне пластины интерферометра относительно оси Y 2 (1), относительно оси X 2 (2)

При наклоне пластины 2 относительно Y2 имеем

φ И ( α х , α у , ξ , ζ ) = φ 1 ( α х , 0, 0, 0) – φ 2 ( α х , 0, ξ , 0).

Графическая зависимость φИ от αх, как следует из рис. 6, достаточна прямолинейна на участке, значительно превышающем практически используемую апертуру наблюдения 2αН. Производная 6фИ !бах (рис. 7) постоянна на этом участке.

Для случая вращения пластины 2 относительно Х 2 график зависимости разности фаз и производной от угла α у носит существенно нелинейный характер, что приводит к деформации интерференционного поля и погрешности считывания информации. Результаты проведенного анализа подтверждают правильность выбора оси наклона пластины интерферометра относительно оси Y 2 , сформулированного на основании приближенных оценок.

ПРЕДЕЛЫ ИЗМЕРЕНИЙ ВЕЛИЧИНЫ СМЕЩЕНИЯ

Максимальная величина измеряемого смещения

Проведенный выше анализ разности фаз лучей на выходе интерферометра позволяет определить подход к анализу диапазона измерений величины вектора смещения.

Амплитуда сигнала рассчитывается по формуле

α _Н

U = J cos [^ ( ^a x , ^a y , £ ) ] d ^a x .        (7)

^{- a} Н

Рассчитанные зависимости амплитуды сигнала U от угла наклона представлены на рис. 8.

В процессе измерений вектора смещения интерферометр настраивается таким образом, что

φИ(αх, ξ) = φ(αх, d), где φИ(αх, ξ) — разность фаз лучей, вносимая интерферометром и определяемая формулой (6); φ(αх, d) — разность фаз лучей от соответственных элементов поверхности при восстановлении изображения объекта с голограммы.

Поскольку настройка интерферометра сдвига производится по максимуму величины выходного сигнала, который определяется минимально возможным градиентом фазы составляющей по эффективной апертуре фотоприемника, связь между величиной смещения и углом наклона можно получить из линейных соотношений [11– 16]. Отсюда dn 1 5 = 17 .

h 2 n ²

Подстановка полученного выражения для ξ в (7) дает прямую зависимость амплитуды выходного сигнала от величины смещения.

Графическая зависимость амплитуды выходного сигнала от величины смещения представлена на рис. 9. Задавшись количественным критерием экстремального падения амплитуды выходного сигнала, можно обозначить верхнюю границу диапазона измерений. Так, если допустить, что амплитуда выходного сигнала не может быть меньше 1/10 своего максимального значения, из рис. 9 следует, что верхняя граница диапазона измерений величины вектора смещения равна 1.5 мм.

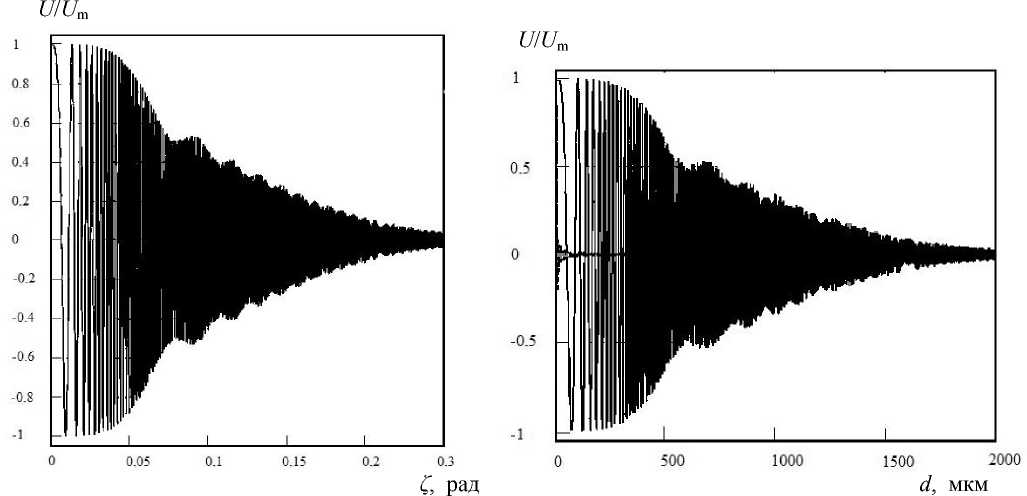
Рис. 8. Зависимость амплитуды выходного сигнала интерферометра от угла наклона пластины

Рис. 9. Зависимость амплитуды выходного сигнала интерферометра от величины измеряемого вектора смещения

Минимальная величина измеряемого смещения

Погрешность определения вектора смещения находится из следующего выражения:

δ d = λδϕ , 2 π sin α ₀

где δφ — погрешность определения фазы интерференционных полос.

Как следует из рис. 1, погрешность определения фазы интерференционных полос при малых d определяется влиянием дополнительных интерферирующих источников и составляет ~ 0.02·2π рад. Поэтому для нижней границы определяемого смещения с использованием (8) можно получить следующую оценку: при λ = = 0.63 мкм, α 0 = 0.1 рад, d И = 0.01 мкм.

ЗАКЛЮЧЕНИЕ

Таким образом, представленное исследование интерферометра поперечного сдвига в фазоизмерительных приборах и системах расшифровки голографических интерферограмм имеет огромное практическое значение для оптического приборостроения. Впервые проведен анализ влияния перекрестной интерферометрии на точность измерений, а также приведены границы применимости интерферометра. В работе получены выражения для максимальной и минимальной величин измеряемого смещения, что позволяет определить класс контролируемых объектов.