Исследование изгибно-продольных колебаний роторов бытовых машин при упругой подвеске

Во многих механизмах основные рабочие органы представляют собой быстро вращающиеся детали – роторы (центрифуги, якоря электроприводов, детали на осях и т.д.). При вращении на больших скоростях как вращающиеся так и неподвижные детали зачастую подвергаются колебаниям. В подавляющем большинстве случаев вибрации возникают вследствие несбалансированности вращающихся деталей. Колебания вызываются периодическими силами, возникающими из-за периодических толчков и больших ускорений периодически движущихся неуравновешенных масс.

Причинами возникновения вибраций также могут быть неправильная центровка соединяемых валов, неточность выполнения элементов кинематических пар и их изнашивание в процессе эксплуатации, люфты в соединениях механизмов, неправильный выбор конструктивных и динамических параметров системы, в результате чего из-за неизбежных деформаций звеньев могут возникать резонансные явления.

Существует большое количество методов для изучения динамических характеристик вращающихся элементов машин, в которых измерение вибраций сводится к измерению частоты колебаний, амплитуд смещения, скорости и ускорения, фазы колебания и т.д.

Однако остается актуальным создание новых устройств для изучения динамики роторных машин, отвечающих современным требованиям, а также методов расчета и улучшения динамических параметров этих механизмов в зависимости от их эксплуатационных условий.

При силовом воздействии на вращающийся ротор в каждом из слоев возникнут нормальные деформации ε jj обусловленные изгибом a( x – r ) и продольной силой b :

ε zz,j = ai(x – r)ejωt + bi ej(ωt-φ);       (1), где εxx,j = εyy,j= σε zz,j .

Тогда тангенциальная деформация

8 xy , i — 8 xz , i — 8 yz , i   0 .          (2).

xy ,        xz ,        yz ,

Нормальным деформациям соответствуют напряжение zz,i    Ei[a(x   r)ej( t i)   bei( t i )], xx,i        yy,i        xy,i        xz,i        yz,i , где    сдвиг фазы между продольными деформациями стержня, r координата нейтрали. Средняя за период и потеря энергии х сечения i-го слоя составят zz,i zz,i

T ,    , dt E [a (x   r)...

W1       2             i.

i T

0  ...2ab(x  r)cos b2];(4)

T

^W         zz , i

zz,i dt     Ei [a2 (x   r)2...

...  2ab(x  r) cos

Суммирование по совокупности всех слоев 1 приводит к соотношениям, характеризующим колебательный процесс стержня в целом: _n    x _i

F          _zzdx  b Re ^{j (    )} aQe ^j . (6)

^{i 1 x} i 1

Изгибающий момент n xi

M        ( x  r ) _zz dx  bQe ^{j (    )} aBe ^j .(7)

i 1 x _{i 1}

Средняя за период энергия n xi

W        Wdx   ( a ² B  2 ab cos Q  b ² R ).

i 1                 ⁴

xi 1

Потеря энергии за период n   xi

W       W dx   ( a ² B  2 ab cos Q  b ² R ).

i 1 x _{i 1}

Декремент колебаний

W     a2B  2abcos Q  b2R d                                                  ,(

4 W     a ² B  2 ab cos Q  b ² R

10) где:

nn

Q      E i P i ; Q      E i P i ;

i 1                          i 1

_P    ( x_i r )²   ( x_{i 1} r )² ;

i ₂

R'

B B B ; tgV     ;

B nn

B       E_iI_i ; B       E _i I _i ; (11).

i 1                         i 1

Здесь P i , I i —статический момент и момент инерции сечения i-го стержня относительно общей нейт р альной оси.

Величины F и М могут быть представлены в матричной форме

F

M

Re i

Qe i

Qb

Ba

(12),

где R — отношение продольной силы к продольной деформации ротора, т. е. жесткость на растяжение; В вел(и5-) чина отношения изгибающего момента к изгибной деформации, т. е. жесткость на изгиб; Q отношение изгибающего момента к продольной деформации.

При соблюдении независимых условий,

_Qⁿ_EiPi    ⁿ_Ei ( x i    r )²   ( x i 1    r )²    ₀ (13)

i1              i1

и Q n EP n E (xi  r)2 (xi 1 r)2

i1              i1

Равенства (13) и (14) удовлетворяются при выполнении условий Ei E const , Ei E const , обо- значающих переход к однородному стержню при выполнении условия i Ei Ei const .

Последнее означает равенство коэффициентов потерь составляющих слоев при неравенстве E и E . В момент, когда колебательная скорость i - го слоя равна нулю, модуль упругости равен значению его активной составляющей.

Когда же скорость максимальна, м одуль упр угости приближается к

E2 E 2 E tg .

В отсутствии потерь, или в момент времени, когда скорость колебаний равна нулю, положение нейтральной сои определяется уравнением ni

Eihi     hp   hi r i1        p1        2

n Eh ii i1

r

В момент времени, когда колебательная скорость максимальна, нейтральная плоскость будет занимать крайнее положение, определяемое величинами E = Ei (1 + ihi ) :

ni

Eihi     hp i1        p1

i     iEihi     hp   hi i1           p1       2

h 1 + a|(2+j3) + i[n2oc|3(2 + p)]

2        1 + a |3 + ia$n

получим при Ct«1, P, T|~1,

n

E i h i i 1

Принимая в (6 - 10) для чисто продольных колебаний а =0 и для чисто изгибных колебаний b =0, получим соотношения для продольных и изгибных

сил.

Аналитические исследования колебаний ротора позволяют рассчитать следующие параметры колебательной системы в зависимости от набора приме-

няемых в конструкции материалов и геометрии. Относительный прирост реактивной и активной составляющей жесткости стержня при внесении демпфи-

рующего материала с относительным ве-

сом ц

R-E 1 h 1   M - p 1 h 1 _ R-E1 h 1 p 1 _

E 1 h 1   "   p 1 h 1      M-p_x h 1 EV

R"-E"₁h 1 ,M-p_x h 1 _ R"-E"\ p 1 , E 1 h 1   '  p_x h 1   ~ M-p_x \ E ^;

Отношение абсолютного прироста временного и пространственного коэффициентов потерь к относительному весу демпфирующего материала

П-П 1 Ц

n iEihi i 1

n

Eihi i 1

i

P 1 h   ;

M- P1 h 1

y-y!_л I® B” ⁴ M    ту,      P| h 1    .  (18)

и      ⁴     в- 54     I e h ;   M- Pt h 1

.           12pT_

Оценим порядок величины смещения нейтральной плоскости в процессе колебаний. Для этого возьмем составной стержень, состоящий из стальной основы и вибропоглощающего слоя. Приняв Ct = E 2,/ ^E „ p = h ₂, !h_x =2, n 1 = 0, T|2 = 1,

И переписав (16) в виде

1 + pap (2 + P)L

. 2 P'"

...»r(1 + 2,5-10"3) . (20)

Как показали исследования, относительное изменение декремента затухания вследствие смещения нейтральной плоскости составит около 0,5%. Среднее за период смещение нейтральной плоскости в л /2 раз меньше максимального.

Поправка на смещение нейтральной плоскости станет существенной лишь при некоторых типах особо жестких демпфирующих материалов. Например, в качестве вибропоглощающего слоя можно использовать вместо резины поропласт.

Таким образом, используя данные теоретических исследования, можно эффективно применять комбинации виброизолирующих и демпфирующих прокладок для получения наибольшей устойчивости ротора в опоре с минимальными отклонениями траектории его верха с учетом изгибно - продольных колебаний и применения упругой вставки.

При проведении аналитических исследований динамических параметров роторов выявлено, что представление колебательной системы - ротор с упругой подвеской позволяет разработать аналитическую модель в виде составного стержня из жестких слоев. Представленная аналитическая модель позволяет предложить упрощенный вариант расчета, используя лишь данные о комплексных модулях упругости и декрементах колебаний.

Метод расчета диссипативных параметров позволяет учесть изгибные и продольные колебания стержня и позволяет получить основные формулы для расчета параметров жесткости стержня в зависимости от используемых различных

h1 1 + ap(2 + P) I

7   1+ot

демпфирующих и виброизлирующих материалов.

Метод также позволяет перейти к упрощенным показателям в виде соотношения параметров массы и геометрии элементов колебательной системы, а также подобрать оптимальные параметры материала подвески ротора. Исследования позволяют дать практические рекомендации для снижения амплитуды отклонений и позволили установить, что применение методов неразрушающего контроля колебаний обеспечило оперативно и с достаточной степенью точности провести комплекс исследований динамических параметров роторов.

При испытаниях вибрационных параметров роторов показано, что замена наполнителя из резины на полиуретан существенно снижает амплитуды отклонений верха оси, что подтверждает аналитические, расчетные и экспериментальные исследования, рис.1. На рис. показана эффективность демпфера на резонансных частотах

Исследование энергетических параметров показало, что энергоемкость роторов существенно растет в период разгона и на резонансах и снижается при достижении рабочих частот. Исследования по совершенствованию эксплуатационных параметров базовых устройств позволили сделать вывод о необходимости изменить конструкцию верхней части гнезд подшипников веретена, что исключает разогрев и преждевременное его разрушение.

При исследованиях по увеличению долговечности верхней опоры роторов отработаны методы крепления датчиков температуры на тормозе стенда и на наружном кольце подшипника. При испытаниях роторов на диссипацию выявлено, что независимо от конструкции амортизатора энергопотери связаны лишь с переходным динамическим процессом. Опытные конструкции показали положительные результаты при производственных испытаниях в течение года.

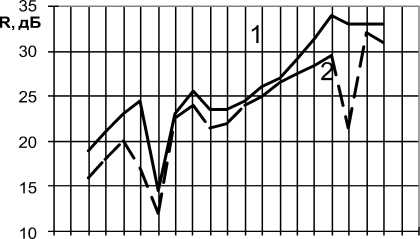
125  250  500  1000 2000 4000

частота, Гц

Рисунок 1 – Виброакустическая эффективность демпферов из разных материалов:

1 – Спектр при установке демпфера из пористого полиуретана; 2 – Спектр при установки демпфера из резины