Исследование излучения атома водорода под действием импульса титан-сапфирового лазера

Ридберговские состояния вследствие большой удаленности от атомного ядра, высоких значений главного квантового числа являются классическим пределом атома. Ридберговские атомы имеют макроскопические размеры, макроскопическое время жизни и экстремально слаб ую связь электрона в атоме, по причине близости энергетических уровней возбужденного электрона к континууму, отличаются высокой чувствительностью к воздействию внешних электромагнитных полей. Волновые пакеты, включающие ридберговские состояния, характ е-ризуются черт ами одновременно и квантовых, и классических объектов: им может быть свойственна локализация в пространстве, эволюция вдоль классической кеплеровской траектории.

Особые свойства таких состояний определяют их применение для изучения принципа соответствия классического предела атома, установления связей между орбитами классически хаотических систем и движением квантового волнового пакета, для решения задач управления поведением ридберговского электрона [1], сжатия электромагнитного поля в резонаторе [2]. В последнее время ридберговские атомы исследуются в качестве источников и детекторов излучения в терагерцовом диапазоне [3-4], имеющем важное значение для биофизики и материаловедения.

Были предложены различные способы теоретического описания ридберговских волновых пакетов [5] и методы их экспериментального получения, основанные на взаимодействии атома с различными комбинациями специально подобранных внешних полей [6-11].

Один из способов получения ридберговских волновых пак етов под разумевает д ействие на атом водорода короткого лазерного импульса высокой интенсивности [8-11]. Данный метод интересен тем, что открывает возможность формирования локализованных волновых пакетов, ограничиваясь только лазерным возбуждением, в отличие от других сложных технологий. Особую актуальность такая методика приобретает в настоящее время в связи с созданием сверхмощных лазерных систем [12] с параметрами, подходящими по интенсивности для решения исслед уемой проблемы.

В данной работе представлены результаты численного моделирования взаимодействия импульса титан-сапфирового лазера с атомом водорода. Ис-след ует ся возможность формирования локализованного волнового пакета под действием лазера. С уч е-том сверхмалой длительности импульса и высокой интенсивности лазерного поля были рассмотрены как переходы на дискретные уровни, включая состояния с высокими значениями квантовых чисел, так и переходы в состояния непрерывного спектра.

Особенностью рассматрив аемой задачи является то, что несущая частота титан-сапфирового лазера существенно отличается от частот переходов между состояниями дискретного и непрерывного спектра. Мы имеем дело со сверхсильным, сверхкоротким и сильно нерезонансны м воздействием на атом, что вызывает необходимость прямого непертурбативного решения уравнения Шредингера и практически исключает интерпретацию результатов в терминах переходов с поглощением/испусканием определенного числа фотонов.

На основе полученного решения уравнений для амплитуд заселенностей исслед уются спектральные характеристики излуч ения атома и возможность генерации в терагерцовом диапазоне под действием импульса титан-сапфирового лазера. Для решения этой задачи рассматривается временная эволюция среднего значения дипольного момента и рассчитывается его спектр Ф урье.

Модель взаимодействия атома водорода с лазерным импульсом

Для исследования динамики заселенностей в атоме численно решается уравнение Шредингера для амплитуд заселенностей в базисе стационарных состояний атома водорода дискретного и непрерывного спектра. Для ограничения числа уравнений непрерывный спектр задается в дискретном представлении [11] с использованием набора состояний, заданных через равные значения волнового числа k . Всего учитывалось двадцать состояний непрерывного спектра с энергиями от 0 до 0,3 в атомных единицах.

Ранее другими авторами [12] было показано, что дипольное приб ли жен ие действует для переходов межд у уровня ми со значениями главных квантовых чисел до 20. Поэтому исследование динамики заселенностей под действием лазерного поля выполня лось для дискретных уровней со значениями главного квантового числа n = 1 + 20. Лазерное поле предполагается циркулярно-поляризованным, поэтому в испо льзуемую модель включены то лько переходы, соответствующие правилам отбора A l = 1, A m = 1, где l и m - орбитальное и магнитное квантовые числа. Предполагается , что перед действием импульса атом находится в основном состоянии . Волновая ф ункция такой системы мо жет быть представлена в виде суперпозиции собственных состояний дискретного и непрерывного сп ектра атома водорода [11]:

Ж t) = ££ C„ (t) RnlYl, m=I + n l=m ZIA

+ЕЕ Ckl (t)RklY,m = W , k l=m где Сnl (t) и Сkl (t) – амплитуды заселенностей дискретных уровней и состояний непрерывного спектра; Rnl, Rkl – радиальные ф унк ции состояний дискретного и непрерывного спектра; Yl,m – сферическая функция; wk = k2Ak - весовой множитель.

Первая сумма в выражении (1) представляет стационарные состояния, вторая – состояния непрерывного спектра. Для учета необратимого характера ионизации в уравнения для амплитуд заселенностей вводилась феноменологическая ширина уровня для состояний непрерывного спектра:

Г к =AE_k a, (2)

где AE_k = E_{k + 1} - E_k , E_k - энергия состояния для данного к ; a - константа. Нами выполнялось исследование для a = 1.

Возможность формирования волновых пакетов, включающих состояния с высокими значениями орбитального и магнитного квантовых чисел, возникает в процессе многократных переходов между состояниями континуума и дискретными уровнями [13]. Для описания подобных эффектов требуется включение в рассмотрение состояний с различными значениями l и m и учет всех возможных переходов между ними, в том числе так называемых «горизонтальных» переходов между подуровнями с одинаковым главным квантовым числом n , но различными орбитальными и магнитными квантовыми числами. С этой целью рассматривались состояния дискретного и непрерывного спектра с l и m до 10. Учитывались все возможные переходы между ними. Система уравнений для амплитуд заселенностей в этом случае может быть представлена в виде (3)

dCnTt) = iЕ Е dnkl±1 exp [±i (-i- Ek) t] x dt           к l '=l ±1

xE (t)• Ckl ±1( t) wk +

EX ' J n' l ±1      Г • / 1      1 Л T',/.z\ Z~'/

Е dnl explz (-2- - ) t IE (t ). Cn'l ±1( t), n' l '= l ±1                  LJ dCkl (t)

= ^- T ^{C kl (} t )⁺

+iЕ Е di±1 expГ±i(-n2 - Ek) t] E(t). Cnl±1(t), n l '=l ±1                 Lj ikl±1 in'l±1 ini±1

где d_nl , d_nl , d_kl – дипольные матричные элементы переходов; E ( t ) – напряженность внешнего электрического поля. Огибающая импульса задается гауссовой формой E(t ) = E 0 • exp[-(2( t - 1 ₀) / T )² ]sin(® t ), T – продолжительность импульса, E ₀ – амплит уд а импульса, to - его частота, 1 ₀ - соответствует центру импульса. Для моделирования использовались параметры импульса существующей мультитера-ваттной лазерной системы [14].

Такой подход позволяет удовлетворительно описать динамику заселенностей в системе. Необходимо отметить, что в выражении (3) при n ' = n подразумеваются переходы между под уровнями с одинаковым значением главного квантового числа.

Предполагается, что атом в начальный момент времени находится в основном состоянии. Поэтому начальные условия к системе уравнений для амплитуд заселенностей (3) могут быть представлены в виде: C ₁₀ (0) = 1, для n = 1, l = 0; C_nl (0) = 0, для состояний дискретного спектра с n = 2 ^ 20; C_kl (0) = 0 для всех состояний непрерывного спектра.

Уравнения (3) решались численно, на основе метода Рунге-Кутта четвертого порядка с использованием программного пакета Mathematica 6.0.3.

Результаты численного моделирования

Исследования динамики заселенностей в системе показали, что под действием импульса с амплитудой 4,59·108 В/см, длиной волны 780 нм и продолжительностью 48 фс [14] наблюдается практически полное опустошение основного состояния (1,8%). Основная часть заселенности (=72%) теряется в результате ионизации . Оставшаяся часть распределяется межд у дискретными уровнями с различными значениями главного, орбитального и магнитного квантовых чисел. Распределение заселенностей дискретных уровней по l и m представлено на рис. 1, а по n – на рис. 2. Поскольку несущая частота импульса принадлежит ближней инфракрасной области и намного меньше частот переходов из основного состояния в возбужденные, естественно, заселяются низко-лежащие возбужденные уровни, однако заметную заселенность приобретают и уровни с n от 10 до 16.

Снижение величин заселенностей при l и m , равных 7 и 9, заметное на рис. 2, является следствием переходов между дискретными уровнями и состояниями непрерывного спектра. В этом случае преимущественно заселяются состояния непрерывного спектра с нечетны ми значениями орбитального и магнитного квантовых чисел, а обратные переходы заселяют дискретные уровни с четными l и m .

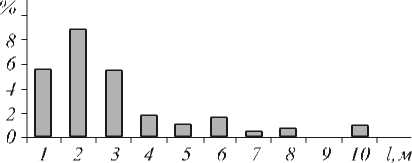
Рис. 1. Распределение заселенностей в процентах по l и m в атоме водорода под действием импульса титан-сапфирового лазера продолжительностью 48 фс, с длиной волны 780 нм и амплитудой 4,59·108 В/см

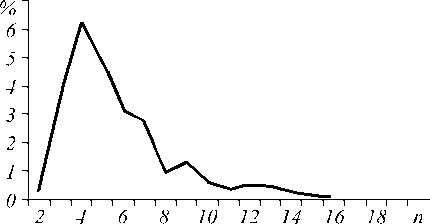
Рис. 2. Распределение заселенностей в процентах по n в атоме водорода под действием импульса титан-сапфирового лазера продолжительностью 48 фс, с длиной волны 780 нм и амплитудой 4,59·108 В/см

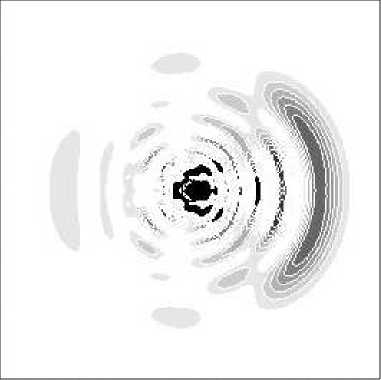
Распределение плотности вероятности волнового пакета, сформированного в результате действия импульса, представлено на рис. 3. Полученное состояние, как видно из рисунка, характеризуется частичной локализацией как по угловой, так и по радиальной переменной. Такая форма пакета также объясняется значительным вкладом в суперпозицию низ-колежащих уровней.

Изучение спектральных характеристик излучения атома

Ранее во введении говорилось, что ридберговские атомы рассматриваются как источники и детекторы излучения в терагерцевом диапазоне, находящего применение в материаловедении и биофизике. Волновые пакеты, включающие ридберговские состояния, также могут представлять интерес в этом смысле. В ходе проведенного анализа выяснилось, что под действием лазерного импульса близки е к терагерцевому диапазону переходы межд у возбужденными уровнями, также как и «горизонтальные» переходы, вносят значительный вклад в динамику заселенностей.

о

-100

-200

-300

-300 -200 -100    0    100 200 300

Рис. 3. Распределение плотности вероятности в атоме водорода под действием импульса титан-сапфирового лазера продолжительностью 48 фс, с длиной волны 780 нм и амплитудой 4,59·108 В/см

Классическое спектральное разложение интенсивности дипольного излучения имеет вид

I ₌ d ε ω ₌ 1 4ω⁴ I _d ^{2 ω} d ω 2π 3 c ³ d ω ^,

где d ε_ω – количество энергии, излученной в единицу времени в интервале частот d ω /2π ;

T – продолжительность импульса;

1T d =   d(t)e dt – Фурье-компонента дипольного

T 0

момента.

В качестве излучающего дипольного момента рассмотрим квантовое среднее d ( t ) = (Ψ( r , t ) d Ψ( s , t ) оператора d дипольного момента атома, где Ψ(r,t) – волновая функция системы, определяемая выражением (1).

Исследование проводилось для импульса титан-сапфирового лазера продолжительностью 48 фс, с центральной длиной волны 780 нм и амплитудой 4,59·108 В/см. Средние значения дипольного момента системы были получены численным инт егриро-ванием для 200 равноотстоящих моментов времени. В разложение волновой функции (1) включались собственные состояния дискретного и непрерывного спектра, умноженные на соответствующие амплитуды вероятности, полученны е в результате численного решения уравнений (3). При интегрировании не учитывались состояния дискретного и непрерывного спектра, число атомов в которых составляло менее 0,0025% первоначального. При этом исключалось большое число состояний непрерывного спектра, так как их заселенность быстро терялась вследствие заданной в используемой модели диссипации. В ременная эволюция среднего значения дипольного момента в атомных единицах представлена на рис. 4.

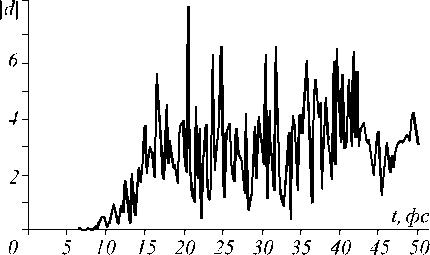
Рис. 4. Динамика среднего значения дипольного момента (в атомных единицах) под действием импульса титан-сапфирового лазера продолжительностью 48 фс, с длиной волны 780 нм и амплитудой 4,59·108 В/см

По рассчитанной временной последовательности средних значений дипольного момента был найден его Фурье-образ d _ω (рис. 5), зависимость которого от частоты ω свидетельствует о том, что основная часть испущенных квантов при ходится на низкочастотное излучение, в том числе в терагерцевом диапазоне.

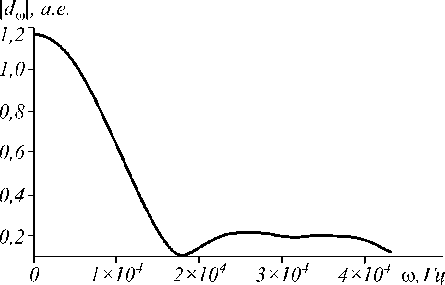
Рис. 5. Фурье-спектр дипольного момента атома водорода под действием импульса титан-сапфирового лазера продолжительностью 48 фс, с длиной волны 780 нм и амплитудой 4,59·108 В/см

Заключение

В результате действия импульса титан-сапфи-рового лазера при реальных значениях продолжительности, амплитуды и частоты импульса может быть сформирован волновой пакет, включающий состояния с различными значениями главного, орбитального и магнитного квантовых чисел. Основная часть заселенности при этом теряется вследствие ионизации, заметно заселяются также низколе-жащие уровни. Тем не менее титан-сапфировый лазер может применяться для формирования волновых пакетов, характеризуемых частичной локализацией как по угловой, так и по радиальной переменной и включающих одновременно с ридберговскими низ-колежащие состояния атома. Повысить значения квантовых чисел во всех степенях свободы возможно с помощью цуга сверхкоротких импульсов [15-16]. Последующие импульсы обеспечивают рост как главного квантового числа, так и орбитального и магнитного квантовых чисел. Снизить ионизационные потери позволяет применение еще более коротких импульсов с частотой в оптическом диапазоне [1516]. Спектральный анализ индуцированного импульсом среднего дипольного момента атома, меняющегося во времени, указывает на наличие широких полос, в том числе в низкочастотной области спектра.