Исследование изменения пластической анизотропии и кристаллографической структуры на различных этапах производства листов из технического алюминия

Характерной особенностью алюминиевых сплавов является склонность к формированию в листах при прокатке структуры с неблагоприятной кристаллографической ориентацией, что вызывает значительную анизотропию деформационных характеристик [1]. При последующем формообразований изделий из таких материалов происходит преимущественное развитие деформации по толщине листа и его разрушение, искажаются форма и размеры изделий, возникает фестонообразование и разно-толщинность стенки детали по его высоте, что в конечном итоге приводит к завышению размеров заготовок, увеличению веса конструкций [2-4]. Предлагаемые решения этих проблем

сводятся, как правило, к механическому учету фактора анизотропии в технологических расчетах и рекомендациям по соответствующей корректировке формы и размеров заготовки и инструмента [5-8].

С другой стороны, перечисленные выше недостатки алюминиевых сплавов могут быть устранены, если при прокатке целенаправленно формировать кристаллографическую ориентацию структуры с учетом требований процессов последующего формообразования заготовок в условиях конкретного напряженно-деформированного состояния [1, 9]. Однако, для решения этой задачи в технологических расчетах необходимо использовать показатели, количественно характеризующие кристаллографическую ориентацию.

Для характеристики направления преимущественного развития деформаций при пластическом течении широко применяются деформационные показатели анизотропии, к которым относятся коэффициенты Пуассона в пластической области или коэффициенты поперечной деформации, представляющей собой отношение логарифмической деформации по ширине к деформации по длине образца при его одноосном растяжении [1]. Как видно из определения, хотя коэффициенты поперечной дефор- мации характеризуют пластическую анизотропию материала, они не учитывают физических основ возникновения анизотропии свойств, т.е. кристаллографической ориентации структуры. А значит – не позволяют решить обратную задачу, т.е., исходя из требований пластического формообразования заготовок, определить наиболее эффективный состав компонент текстуры, который необходимо сформировать в процессе производства конструкционных материалов.

В связи с этим, в данной работе установлена взаимосвязь между значениями коэффициентов поперечной деформации и параметрами преимущественной кристаллографической ориентации структуры, а также на примере прокатки технического алюминия Al99 исследовано изменение кристаллографии структуры и показателей анизотропии.

ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Воспользуемся критерием пластичности, в основные уравнения которого введены параметры строения материала [9]:

22 { ⁿ 12 ⁽ ° 11 - ° 22 ) ^{+ n} 23 ( ° 22 - ° 33 ) ^{+ П} 31 ⁽ ° 33 ^— ° 11 ) ⁺

+ 4

5 I 2      I 5 I 2 I 5 I 2

2 - - 7 12 I ° 12 + 1 2 - ⁿ 23 I ° 23 + 1 2 - ⁿ 31 I ° 31

где ° i - интенсивность напряжений; °y -компоненты тензора напряжений; ( i, j = 1, 2, 3; 1 – направление проката, 2 – поперечное направление; 3 – направление по толщине листа); Пу - обобщенные показатели анизотропии:

15 (A —1)I

П» — 1^i + А— Al     ;

ij        3 + 2 A ' ( i j k 5 J

A - параметр анизотропии кристаллической решетки:

A — SUU—Sm;

2 ^S 2323

S ijkl

– упругие константы кристаллической решетки;

А i - параметры кристаллографической ориентации структуры:

_А i _—    £   p ^{{ hkl} К ^uv w а^ К ^uv w _;    (4)

{ hkl }^ uvw^

{ hkl }( uvw^

^p – весовая доля i -ой компоненты { hkl } ( uvw ); A ^{{ hkl }} uvw^ – ориентационный фактор идеальной кристаллографической ориентировки { hkl } ^ uvw ^:

,9,9  ,9,9  ,9,9

{ hkl }( uvW) _ h i k i + k , l , + 1 , h i ,

^А i                    i                    \ 2 ^;

( h ² + k ² + l² )

h _i , k _i , l _i – индексы Миллера, определяющие i -е направление в кристалле относительно системы координат, связанной с образцом.

При использовании критерия пластичности (1) уравнения связи между линейными деформациями Ey и напряжениями ° ij с учетом параметров строения материала имеют вид:

^E 11 ^— Т~ ^{[ п} 12 ⁽ ° 11 ^— ° 22 ^{) + П} 31 ⁽ ° 11 ^— ° 33 ) ] ,

2 °i e22 — Т“i“[п12 (°22 — °11) + п23 (°22 — °33 )], (6) 2 °i

^E 33 ^—Т“^{L[ п} 23 ⁽ ° 33 ^— ° 22 ^{) + П} 31 ⁽ ° 33 ^— ° 11 ^)] ,

2 °i где Ei - интенсивность напряжений.

Определим зависимость коэффициента поперечной деформации от направления в плоскости листа. Рассмотрим растяжение образца, вырезанного под углом ^а к направлению прокатки. В этом случае коэффициент поперечной деформации выражается следующим образом:

Ца — — EO+90^, (7) Еа где Еа+9о» - поперечные пластические деформации сжатия при линейном растяжении плоского образца; Еа - продольные пластические деформации растяжения.

Напряжения и деформации, которые возникают при растяжении образца, вырезанного под углом а к направлению прокатки, связаны следующими зависимостями с напряжениями и деформациями в главных осях анизотропии [10]:

° 11 — °_а cos ² а ,

• 2

° 22 — °_а sin а ,              (8)

° 12 — °_а sin а cos а , 2        .              • 2       .

Е_а — E ncos а + E 22 sin а + E 12 sin а cos а , (9) где °_а - предел текучести при линейном растяжении образца, вырезанного под углом а к направлению прокатки.

Подставляя выражения (9) в (7), с учетом зависимостей (8) и (6) после преобразований получим:

Ц а ^{— 1 — [} П 23 sin^{2 а +} П 31 ^c oS^{2 а ] [} ( П 12 ⁺ П 23 ) ^sin4 ^{а +}

— 1    (10)

.

I 5 I

+ ( П 12 + Л 31 ) cos а + 61 j — n ^,12 J sin а cos а

Используя зависимость (10), можно определить величину коэффициента поперечной деформации в любом направлении плоскости листа, если известны обобщенные показатели анизотропии материала. При этом выражения для коэффициентов поперечной деформации в направлении прокатки, под углом 45° к направ- лению прокатки и поперечном направлении запишутся следующим образом:

;

^п 21 + ^п 31

4Л12 + п23 + п31 -10 ;

4Л12 - п23 - П31 -10

^п 12 + ^п 23

МЕТОДИКА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА

Исследования проводились на слитках толщиной 400 мм из технического алюминия Al99, которые обрабатывались по маршруту, приведенному с указанием режима отжига, температуры нагрева под прокатку и степеней обжатия при горячей и холодной прокатке на рисунке 1. Остальные параметры соответствовали общепринятой технологии прокатки. На каждом этапе производства отбирались образцы для рентгеноструктурного анализа и механических испытаний.

Текстурные измерения в виде построения полюсных фигур осуществляли на образцах, вырезанных из поверхностных и серединных плоскостей по толщине листа. Плоскость съемки полюсных фигур была параллельна плоскости прокатки. Текстуру в виде неполных полюсных

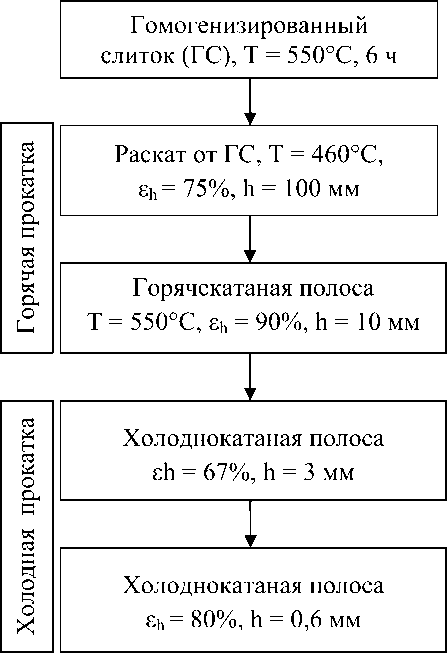
Рис. 1. Схема прокатки слитков из технического алюминия Al99

фигур {111}, {200}, {220} и {311} исследовали методом «на отражение» с использованием рентгеновского дифрактометра в CoK a -излучении. Функцию распределения ориентировок (ФРО) рассчитывали по экспериментальным полюсным фигурам. По полученным ФРО рассчитывали обратные полюсные фигуры для трех взаимно перпендикулярных направлений в образце (направление нормали к плоскости прокатки; направление прокатки; поперечное направление).

Из анализа сечений ФРО определяли преимущественные кристаллографические ориентировки и их объемные доли. Критерием адекватности выбора набора таких ориентировок являлся минимум величины среднеквадратичного отклонения между экспериментальной и рассчитанной по сумме отдельных ориентировок ФРО. Затем по формулам (4) и (5) рассчитывались ориентационные факторы текстуры. На основании результатов текстурного анализа по формулам (11) рассчитывались значения коэффициентов поперечной деформации.

Для изучения пластической анизотропии вырезали по 3 образца на каждое направление под углами 0°, 45° и 90° к направлению прокатки. Размеры образцов выбирались по ГОСТ 11701-84 и ГОСТ 1497-84 в зависимости от толщины листа. Испытания проводили на электромеханической испытательной машине. Коэффициенты поперечной деформации рассчитывали по формуле (7).

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

В результате текстурного анализа установлено, что в раскате из технического алюминия Al99 наблюдается неоднородность текстуры по толщине. Для поверхностного слоя гомогенизированного слитка характерны идеальные ориентировки {110}<233>, {123}<139>, {139}<123> (таблица 1). В центральном слое преобладают ориентировки типа { 127 } (123^ , { 139 } (123) , { 100 } (100). В центральном слое раската наблюдаются преимущественно ориентировки {130}<139>, {139}<123>, {100}<100>, а в поверхностном слое - {139}<123>, {100}<110>, {100}<100>.

Максимальные значения коэффициентов поперечной деформации соответствуют таким ориентировкам, как {110}<233>, {233}<123>, {110}<332>, {332}<203>, {123}<139>, {110}<100>, а минимальные ориентировкам {100}<100>, {100}<110>, {139}<123>, {130}<135>, {130}<139>, то, как видно из таблице 1, коэффициенты поперечной деформации принимают минимальные значения. Выравниванию коэффициентов анизотропии в плоскости проката способствуют ориентировки {110}<233>, {120}<125>, {120}<112>, {126}<124>, {332}<203>.

Таблица 1. Изменение преимущественных кристаллографических ориентировок при прокатке слитков из технического алюминия Al99

Состояние материала	Основные ориентировки { hkl } yivw>	Весовые доли ориентировок p { hkl }( uw	Коэффициенты поперечной деформации ориентировок, p ija (определены по формулам (11))
			№	Ц 1	Ц 12
Гомогенизированный слиток (ГС), Т = 600°С, 6 ч (поверхность)	{110}<233> {123}<139> {139}<123> {100}<100> {120}<125> {130}<135>	0,3812 0,2908 0,1453 0,0702 0,0642 0,0482	0,663 0,500 0,284 0,500 0,401 0,294	0,561 0,480 0,523 0,142 0,484 0,503	0,425 0,715 0,284 0,500 0,523 0,326
Гомогенизированный слиток (ГС), Т = 600°С, 6 ч (центр)	{120}<112> {123}<139> {110}<111> {113}<125> {135}<123> {100}<100>	0,5385 0,2313 0,1457 0,0694 0,0081 0,0071	0,524 0,500 0,500 0,548 0,673 0,500	0,434 0,480 0,614 0,384 0,462 0,142	0,402 0,715 0,380 0,514 0,462 0,500
Раскат от ГС, Т = 460°С, sh = 75%, h = 100 мм (поверхность)	{139}<123> {100}<110> {100}<100> {110}<100> {126}<124> {124}<123>	0,3034 0,3033 0,2184 0,1686 0,0045 0,0019	0,284 0,142 0,500 0,500 0,415 0,414	0,523 0,500 0,142 0,391 0,458 0,552	0,284 0,142 0,500 0,857 0,404 0,414
Раскат от ГС, Т = 460°С, Sh = 75%, h = 100 мм (центр)	{130}<139> {139}<123> {100}<100> {233}<123> {100}<110> {110}<100>	0,3270 0,2981 0,1959 0,1689 0,0073 0,0028	0,421 0,284 0,500 0,541 0,142 0,500	0,387 0,523 0,142 0,640 0,500 0,391	0,489 0,284 0,500 0,567 0,142 0,857
Горячекатаная полоса Т = 550°С, Sh = 90%, h = 10 мм	{100}<010> {139}<321> {320}<001> {125}<311> {331}<323> {311}<233>	0,1056 0,1040 0,0915 0,0742 0,0624 0,0616	0,500 0,284 0,500 0,452 0,474 0,336	0,142 0,523 0,347 0,447 0,635 0,570	0,500 0,284 0,775 0,483 0,432 0,272
Холоднокатаная полоса sh = 67%, h = 3 мм	{110}<332> {100}<010> {139}<321> {123}<153> {211}<111> {311}<011>	0,1365 0,1232 0,1150 0,1035 0,1008 0,0864	0,663 0,500 0,284 0,705 0,499 0,272	0,561 0,142 0,523 0,441 0,614 0,570	0,425 0,500 0,284 0,537 0,380 0,336
Холоднокатаная полоса Sh = 80%, h = 0,6 мм	{100}<010> {311}<233> {135}<132> {110}<111> {123}<139> {332}<203>	0,1540 0,1404 0,1106 0,1104 0,0920 0,0915	0,500 0,336 0,673 0,500 0,500 0,550	0,142 0,570 0,462 0,614 0,480 0,603	0,500 0,272 0,462 0,380 0,715 0,659

Проверка достоверности разработанной модели взаимосвязи показателей анизотропии с характеристиками текстуры осуществлялась путем сопоставления значений коэффициентов поперечной деформации, вычисленных по формулам (11) по данным о текстуре образца и по формуле (7) по данным механических испытаний образцов на рас-

Таблица 2. Сопоставление расчетных и экспериментальных значений коэффициентов поперечной деформации технического алюминия Al99

Исследуемый материал Коэффициенты поперечной деформации расчетные, определены по формулам (11) экспериментальные, определены по формуле (7) cal ^21 cal А1 cal ^12 ^7 ^7 ^7 Горячекатаная полоса, sh = 90%, h = 10 мм 0,516 0,471 0,523 0,462 0,430 0,448 Холоднокатаная полоса, sh = 67%, h = 3 мм 0,422 0,483 0,444 0,392 0,460 0,452 Холоднокатаная полоса, sh = 80%, h = 0,6 мм 0,470 0,508 0,474 0,460 0,489 0,405 тяжение (7) (таблица 2). Расхождения в расчетных и экспериментальных значениях µij не превышают 10% и объясняются разбросом значений полюсной плотности, а также отражают тот факт, что µiejxp характеризуют анизотропию не исходного, а деформированного растяжением образца.

В целом результаты исследований свидетельствуют о достаточно хорошей сходимости расчетных и экспериментальных данных, следовательно модель (10) отражает реальную анизотропию деформационных характеристик листовых материалов, а критерий пластичности (1) адекватно описывает пластическое течение анизотропного материала с учетом его кристаллографической ориентации структуры.

ЗАКЛЮЧЕНИЕ

Проведенные исследования формирования компонент текстуры и показателей анизотропии на основных стадиях прокатки, сопоставление расчетных и экспериментальных значений коэффициентов поперечной деформации подтверждают принципиальную возможность формирования в листах заданной кристаллографической ориентацией структуры, требования к которой можно сформулировать на основании анализа процессов формообразования листовых заготовок с использованием разработанного авторами критерия пластичности.

Исследование выполнено в рамках госзада-ния (тема FSSS-2020-0016).