Исследование явления скольжения в кристаллических материалах методами имитационного моделирования

In the modified barrier model of a constant linear tension all stages of process of origin and propagation of elementary crystallographic slip in a field of discrete obstacles of the dislocation nature are simulated and explored

Среди известных микромеханизмов, лежащих в основе пластичности кристаллов, наиболее распространено явление скольжения. Пластическая деформация скольжения часто выступает как основной или единственный способ формоизменения кристаллов при механических воздействиях на них. В свою очередь, пластичность скольжения является результатом многочисленных кристаллографических скольжений и некристаллографических деформаций, обусловленных диффузионным массопереносом [1]. Поэтому для понимания природы пластичности кристаллов необходим синтез знаний о микромеханизмах пластичности на уровне единичного кристаллографического скольжения, при котором происходит относительное смещение частей кристалла по определенной кристаллографической плоскости и в определенном кристаллографическом направлении на наименьший вектор трансляции решетки в направлении скольжения.

Такой выбор обоснован, прежде всего, потому, что в условиях внешнего механического воздействия на кристалл именно на этом уровне действуют основные движущие силы микромеханики пластичности скольжения – силы Пича – Кёлера. На уровне элементарного скольжения совершается работа этих сил, происходит изменение конфигурационной и кинетической составляющих энергии кристаллической решетки, связанной с его дефектной подсистемой, осуществляется диссипация энергии. При рассмотрении элементарного кристаллографического скольжения как единого целостного процесса может быть в полной мере реализован энергетический подход и применен закон сохранения энергии для получения необходимых характеристик, описывающих это явление.

Распространение элементарного скольжения в объёме кристалла осуществляется посредством перемещения его границы, общепринятой моделью которой, несомненно, упрощенной, является дислокация. Принимая такую модель, вышесказанное означает, что фронт скольжения, распространяющегося в объёме кристалла под действием напряжений, созданных деформирующим воздействием, образует расширяющаяся замкнутая планарная дислокация (дислокационная петля), поэтому динамика кристаллографического скольжения может рассматриваться как динамика связанной с ним дислокационной петли.

Естественным аппаратом для описания распространения элементарных кристаллографических скольжений является понятийный и математический аппарат микромеханики дислокаций, включая его статические, кинематические и динамические аспекты.

При изучении элементарных кристаллографических скольжений появляются трудности принципиального характера. Казалось бы, зарождение и распространение кристаллографического скольжения можно описать на основе уравнений динамики дислокаций. Однако уже описание конфигураций прогибающегося индивидуального дислокационного сегмента в отсутствие препятствий на основе дифференциального уравнения струны возможно лишь до достижения этим сегментом критической конфигурации. В процессе распространения элементарного скольжения ограничивающая его расширяющаяся замкнутая дислокация пересекает десятки тысяч дислокаций других систем скольжения. При контактном взаимодействии дислокаций возникают дефекты дислокации: пороги и перегибы, дислокации вступают между собой в дислокационные реакции [2]. Кроме того, дислокации взаимодействуют с атомами растворенных элементов, частицами второй фазы и т.д. (препятствиями, стопорами). Разумеется, взаимодействие дислокации со стопором оказывает влияние на ее взаимодействие с другими стопорами; то есть задача описания движения дислокации, осуществляющей кристаллографическое скольжение, является разновидностью проблемы многих тел, которая относится к числу неинтегрируемых. Аналитические решения таких задач принципиально невозможны. Далее, дислокации некомпланарных систем скольжения, пересекающие плоскость скольжения, ориентированы и распределены в пространстве случайным (или ещё каким-либо) образом. Учет случайности в расположении препятствий приводит к соответствующим теоретико-вероятностным проблемам, серьёзно усложняя и без того сложную задачу.

Многое дает реальный эксперимент. Но в обсуждаемых вопросах далеко не все: действительные деформационные дефекты структуры, формирующиеся в процессе деформации и осуществляющие ее, существуют в динамике и в сложных взаимодействиях. Экспериментатор же имеет дело с реликтовыми структурами, сохранившимися в материале после релаксационных процессов динамического возврата, и поэтому крайне сложно проследить динамические эффекты. Диаметр элементарных скольжений довольно велик по сравнению с межатомными расстояниями в кристалле: он составляет в реальных кристаллах от десятков до сотен микрометров [3]. В этом проявляется основная трудность наблюдения элементарных кристаллографических скольжений с помощью методов просвечивающей электронной микроскопии. Эксперименты подобного рода уникальны и крайне редки.

Таким образом, многофакторность, сложность и линейные масштабы процесса распространения элементарного кристаллографического скольжения, а также высокая скорость этого процесса приводят к тому, что в настоящее время его не удаётся проследить ни аналитическими, ни существующими экспериментальными методами. Приемлемым выходом из этой ситуации представляется воспроизведение зарождения и распространения элементарного кристаллографического скольжения посредством машинных экспериментов, которые должны описывать: 1) докритические конфигурации дислокационного сегмента, являющегося потенциальным источником при его выгибании под действием внешнего напряжения; 2) прохождение выгибающимся дислокационным сегментом околокритических конфигураций и конфигурации потери механической устойчивости; 3) дальнейшее выгибание дислокации-источника после потери устойчивости, ее замыкание и отделение от нее замкнутой расширяющейся планарной дислокационной петли; 4) расширение отделившейся замкнутой планарной дислокации до диаметра порядка среднего диаметра наблюдаемых экспериментально кристаллографических скольжений; 5) конфигурации дислокаций-источников в начале второго цикла их действия.

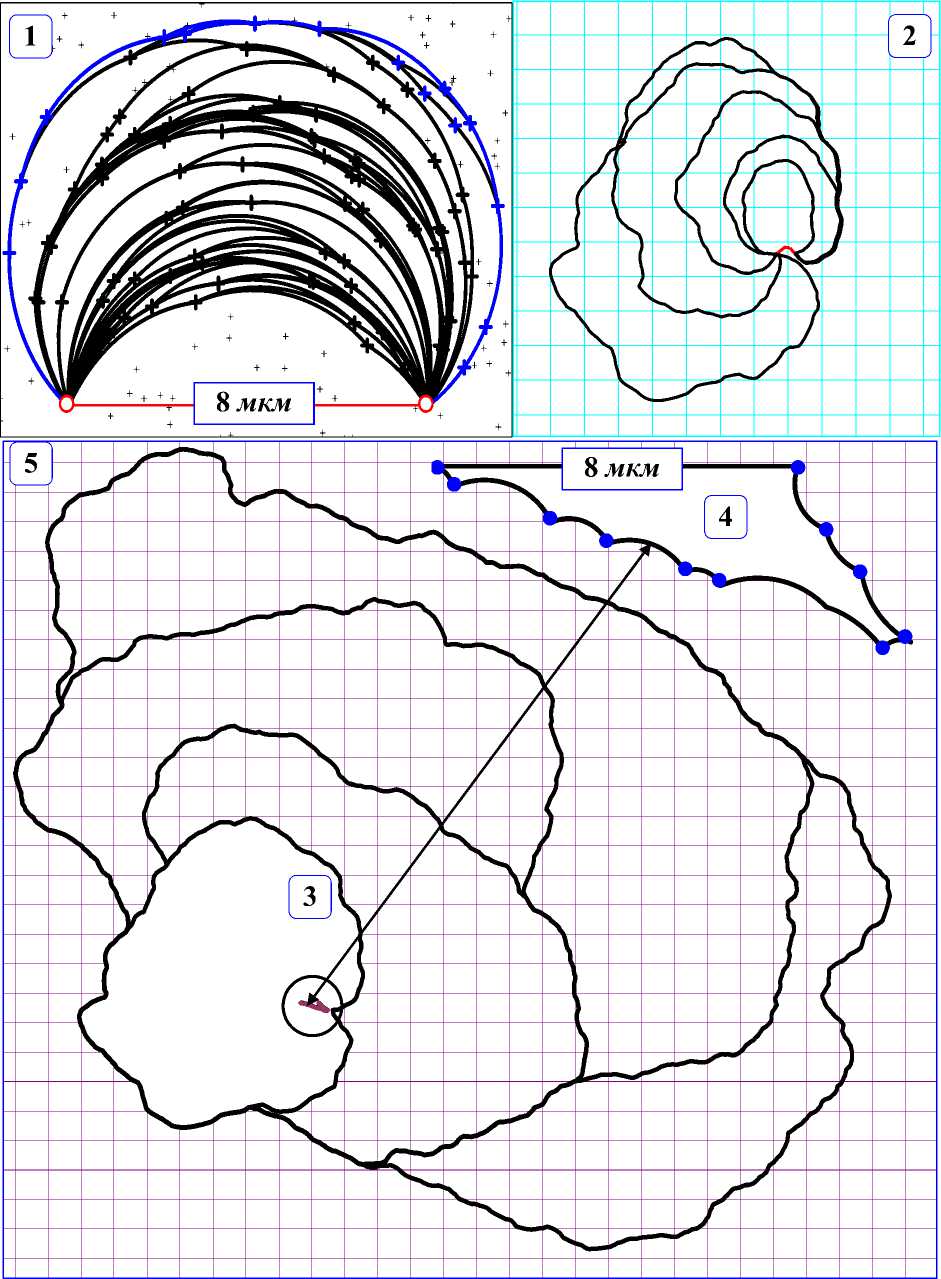
Рис. 1. Эмиссия дислокационной петли сегментом-источником длиной 8 мкм в поле слабых однородных препятствий

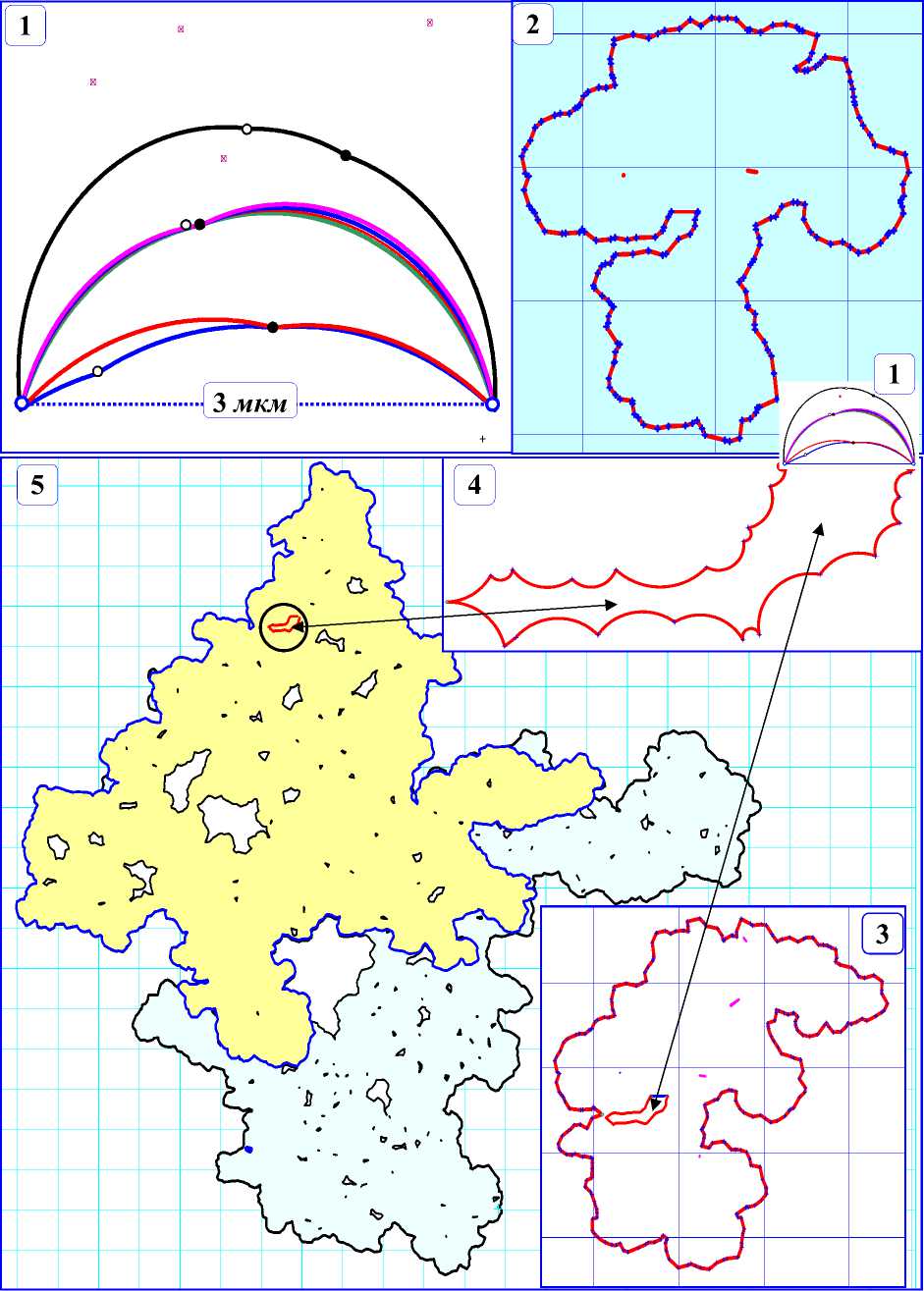
Рис. 2. Эмиссия дислокационной петли сегментом-источником длиной 3 мкм в поле препятствий дислокационной природы (без учёта реакции аннигиляции)

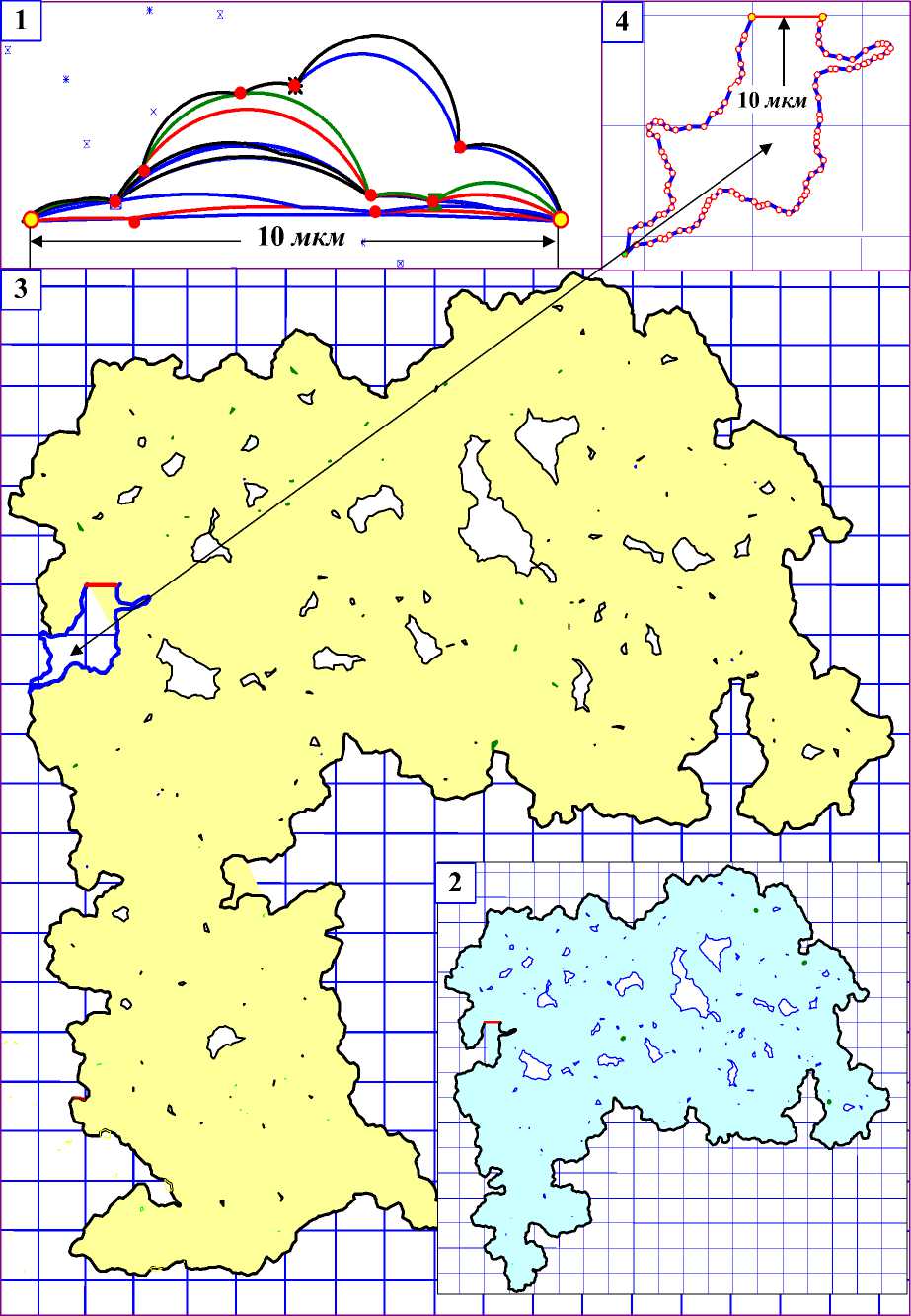
Рис. 3. Эмиссия дислокационной петли сегментом-источником длиной 10 мкм в поле препятствий дислокационной природы (с учётом реакции аннигиляции)

Физическая модель распространяющегося в объёме кристалла единичного кристаллографического скольжения, методика моделирования на ЭВМ расширения связанной с этим скольжением замкнутой дислокации, алгоритмы и программы, позволяющие методами имитационного компьютерного моделирования воспроизводить, исследовать и описывать элементарное скольжение как единый целостный процесс, значения параметров, при которых реализованы машинные эксперименты (применительно к монокристаллам меди ориентированным для множественного скольжения в плоскостях типа {1 1 1} с осью деформации <0 1 0> и исходной плотностью дислокаций некомпланарных систем скольжения 10⁸ см ^-2), приведены в [4, 5]. Отметим здесь только, что в формулировке дислокационной микромеханики это соответствует моделированию действия дислокационного источника и двухмерного процесса расширения замкнутой планарной дислокационной петли, образующей фронт элементарного скольжения, в поле случайно расположенных дискретных препятствий на участке плоскости скольжения, соизмеримым с размерами экспериментально наблюдаемых зон сдвига в реальных кристаллах.

Компьютерные эксперименты проведены в трёх вариантах модели: а) плоскость кристаллографического скольжения содержит только однородные слабые препятствия, прочность которых соответствует нереагирующим дислокациям некомпланарных систем скольжения [6] (рис. 1); б) содержит сильные и слабые препятствия – реагирующий и нереагирующий, соответственно «лес» [7, 8] (Рис. 2); в) в модель б) добавлены препятствия, прочности которых соответствуют реакции аннигиляции [9, 10] (рис. 3). На рис. 1-3: фрагменты 1 соответствуют прогибанию потенциального сегмента-источника в поле препятствий под действием приложенного напряжения до конфигурации потери устойчивости [11]; 2 – последняя из наблюдаемых дислокационных конфигураций, предшествующих моменту замыкания дислокации в дислокационную петлю; 3 – момент отделения дислокационной петли от источника; 4 – восстановленный источник (начальная конфигурация дислокационного источника второго цикла действия); 5 – эволюция дислокационной петли после её образования. Препятствия на большинстве фрагментах рисунков не показаны. В этом случае в каждом квадрате сетки фрагмента в среднем по 225 препятствий.

Анализ и обработка большого числа компьютерных имитаций процесса зарождения и распространения элементарного кристаллографического скольжения позволяют сделать следующие выводы.

В зависимости от длины сегмента-источника, свойств и расположения препятствий в плоскости кристаллографического скольжения атермическое напряжение старта дислокационного источника τ st (минимального напряжения, при котором начинается атермическое необратимое кристаллографическое скольжение) превышает напряжение Франка – Рида [12] в 1,2…6 раз (рис. 4), а вклады в τst , обусловленные полем препятствий и средней кривизной дислокации-источника в момент потери устойчивости, аддитивны, но с определенными коэффициентами (не весами) в их линейной комбинации; строго аддитивное представление возможно при введении поправок на различие соответствующих критических конфигураций и конфигураций потери устойчивости. Поправки пренебрежимо малы в модели слабых однородных препятствий и значимы в моделях дискретных препятствий с дисперсией по прочностям; абсолютная величина поправок возрастает с увеличением длины сегмента-источника [13]. В модели однородных слабых препятствий термические активации уменьшают τ st вплоть до напряжения Франка – Рида τ F -R (минимального напряжения активации источника в отсутствие препятствий) независимо от длины источника. Время достижения конфигурацией потери устойчивости определяется приложенным напряжением и температурой: при низких температурах и τ → τF-R оно становится бесконечно большим по отношению к продолжительности традиционных лабораторных испытаний, при напряжениях, превышающих τF-R всего на 3%, – не превосходит 0,1 с и быстро уменьшается до долей наносекунд с увеличением напряжения и температуры [14]. При наличии в плоскости залегания источника дислокационных препятствий различной прочности роль термических активаций значительно меньше (в среднем они лишь на 9% снижают напряжение начала необратимых кристаллографических скольжений по сравнению с атермическим напряжением старта дислокационного источника). С уменьшением длины источника влияние активационных процессов уменьшается и возрастает доля экспериментов, в которых наблюдаются одинаковые атермические и термоактивационные напряжения старта [15].

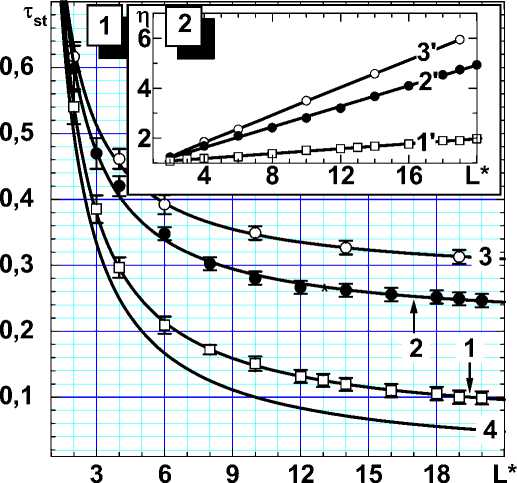
Рис. 4. Атермическое напряжение старта дислокационного источника в зависимости от длины источника L и свойств препятствий: 1 – поле слабых термоактивируемых препятствий, 2 – препятствия дислокационной природы без учета (3 – с учетом) реакции аннигиляции. На фрагменте 2 – соответствующие (та же нумерация со штрихами) зависимости превышения η атермического напряжения старта источника по отношению к напряжению

Временные, масштабные и динамические характеристики элементарного скольжения, полученные при последовательном рассмотрении двухмерной модели, связанной со скольжением замкнутой дислокации с учетом её нелокальной кривизны, имеют принципиальные отличия от представлений, сложившихся на основе рассмотрения движения бесконечных квазипрямолинейных дислокаций. При распространении скольжения баланс сил, обусловленных линейным натяжением и приложенным напряжением, нарушается все в большей степени, движение дислокации переходит в надбарьерный динамический режим. Дислокационная петля быстро ускоряется до скоростей, близких к скорости распространения поперечных звуковых колебаний в кристалле. Квазистационарное термоактивируемое скольжение дислокаций, описываемое традиционными моделями и приводящее к проблеме un-zipping’а [16-18] (эффекта молнии), реализуется лишь в малой области, составляющей менее 0,1% площади дислокационной петли в момент ее отделения от источника. Однако основной вклад в величину времени эмиссии петли вносит время пребывания дислокации в конфигурациях, принадлежащих именно этой области [19]. Другими словами, единичное скольжение в кристалле происходит в две стадии: термоактивируемое скольжение и атермическое скольжение. Стадии разделены конфигурацией потери устойчивости выгибающейся дислокации-источника. Лишь в небольшой части активной плоскости скольжения движение дислокаций осуществляется с помощью тепловых флуктуаций. На всей остальной площади активных плоскостей скольжения дислокации движутся атермически в надбарьерном режиме. Эти результаты подвергают сомнению правомерность относить термоактивационные параметры, найденные из макроскопических экспериментов, ко всему процессу движения дислокаций [20-26].

Распространение кристаллографического скольжения, в зависимости от свойств препятствий, может сопровождаться отделением от скользящей дислокации замкнутых вогнутых дислокационных петель, ограничивающих острова незавершенного кристаллографического сдвига (рис. 2, 3), что приводит к увеличению работы внешних сил в процессе скольжения и может быть причиной дополнительного деформационного упрочнения [27]. Интенсивность процесса петлеотделения определяется, прежде всего, дисперсией прочностей препятствий (в модели однородных слабых препятствий (рис.1) отделения вогнутых петель не наблюдалось), приложенным напряжением и прочностью сильных препятствий (в [28] появление вогнутых петель связано только с прочностью препятствий). В поле препятствий дислокационной природы интенсивность петлеотделения возрастает с увеличением напряжения, а при постоянном внешнем напряжении она увеличивается по мере распространения фронта скольжения [27]. Острова представляют собой кластеры от 3 препятствий до 10 тысяч, преимущественно сильных, концентрация которых вдоль границы острова (вдоль вогнутой петли) почти на порядок величины превышает долю сильных препятствий в плоскости скольжения, а среднее расстояние между препятствиями вдоль вогнутых петель значительно меньше соответствующего значения вдоль расширяющейся дислокационной петли [27]. Преобладающая часть (не менее 92%) вогнутых дислокационных петель, связанных с островами, аннигилирует в динамическом режиме под действием сил линейного натяжения и сил, обусловленных внешним напряжением, и лишь небольшая часть (около 7%) – с помощью термических активаций за время порядка десятков наносекунд. Устойчивые острова в поле препятствий дислокационной природы крайне редки [29]. Поскольку аннигиляция вогнутых дислокационных петель, ограничивающих острова незавершенного сдвига, и все сопутствующие эффекты происходят за время порядка наносекунд, их наблюдение возможно только непосредственно в процессе деформации и только в окрестности фронта скольжения. Острова незавершенного кристаллографического сдвига – концентраторы диссипации энергии в активной плоскости скольжения, так как линейная плотность энергии вогнутой дислокационной петли, связанной с незавершенным скольжением, может на несколько порядков величины превышать линейную плотность собственной энергии покоящейся дислокации. В локальных областях аннигиляции вогнутых замкнутых петель энергетически возможны переход атомов в возбуждённые состояния и связанное с этим электромагнитное излучение [29].

Дислокация-источник обладает определенной кинетической энергией в момент восстановления и под действием сил Пича – Кёлера приобретает дополнительную кинетическую энергию в процессе перехода из этой конфигурации в конфигурацию потери устойчивости сегментом-источником в первом цикле его действия. Поэтому однажды активированный источник вслед за первой дислокацией производит в едином процессе серию замкнутых планарных дислокационных петель, что приводит к локализации скольжения, обусловленной динамическими свойствами дислокаций как замкнутых линейных дефектов. Такая динамическая локализация происходит при деформации скольжения во всех кристаллических материалах и является неотъемлемым свойством кристаллографического скольжения. В [30] на основе анализа геометрических характеристик восстановленных источников и конфигураций потери устойчивости дислокационными источниками установлена зависимость величины динамической локализации скольжения, связанной с активностью одного источника, от длины источника и механизма его действия.