Исследование явных численных методов решения уравнений параболического типа

Оригинальная статья / Original article

EDN:

Разработка новых численных алгоритмов для решения задач теплопроводности имеет большое значение для развития науки и техники, а также для практического применения в различных отраслях промышленности и энергетики. Явные и неявные трехточечные численные алгоритмы1 являются широко используемыми методами для решения таких уравнений. Однако явные схемы имеют серьезные ограничения на шаг интегрирования по времени, а неявные методы не всегда обеспечивают требуемую точность при больших значениях шага интегрирования.

Цель данной работы состоит в исследовании явных численных алгоритмов для решения нелинейных уравнений теплопроводности.

• ¹    Численное решение многомерных задач газовой динамики / С. К. Годунов [и др.]. М. : Наука, 1976. 400 с.; Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. М. : БИНОМ. Лаборатория знаний, 2003. 632 с.

Technical sciences                                                                 65

ОБЗОР ЛИТЕРАТУРЫ

В данной области проведено большое количество исследований. В настоящее время активно развиваются новые алгоритмы решения уравнений параболического типа. Так, рассмотрены принципы построения схем численного интегрирования по времени параболических уравнений [1]. Разработан подход к интегрированию по времени системы нестационарных уравнений динамики сжимаемого теплопроводного газа [2]. Создан метод численного решения нелинейного уравнения, описывающего диффузионный перенос энергии излучения [3]. Алгоритмы решения уравнений параболического типа являются явными с отсутствием диффузионного ограничения на шаг интегрирования по времени, что может значительно увеличить скорость получения результатов при решении практических задач [4–6]. Метод, основанный на использовании многочленов П. Л. Чебышева, позволяет уйти от ограничения шага интегрирования по времени, используя итерации внутри одного шага интегрирования [1]. Метод, основанный на гиперболизации исходного уравнения, заключается в введении в исходное уравнение второй производной по времени, умноженной на малый параметр [3]. В силу явности таких методов для них легко могут быть построены параллельные вычислительные алгоритмы.

МАТЕРИАЛЫ И МЕТОДЫ

Предполагается проведение программной реализация трех численных методов решения уравнений параболического типа: классической явной схемы, метода локальных итераций и метода гиперболизации. Алгоритмы реализованы на языке C++.

Анализ численных алгоритмов для решения уравнений теплопроводности будет проводиться для первой краевой задачи с переменными коэффициентами.

p ( x , t )

a u ( x, t ) __a

<

8 1     8 x ^

^{8 u} ( ^x ■ t ) 1 a x _?

+ f ( x, t ) ,0 <  x <  l ,0 <  t <  T,

u(x,0) = v(x), u(0,t) = Ф1 (t). u(l,t) = Ф2 (t), где функция u(x, t) является искомой; u(x, 0) – начальные условия; u(0, t), u(l, t) – граничные условия.

Рассмотрим пространственно-временную сетку:

ꭥh,τ=ꭥh×ꭥτ , где QT ={tn nт, 0 < n < NJ - сетка по времени с шагом т = T/Nт, Qh = {xi = ih, 0 < i < Nh}; Ωh – пространственная сетка, зависящая от шага сетки h = L/Nh, характеризующего размер ячеек; T – время, до которого ведется расчет; L – длина расчетной области.

Явная схема для уравнения (1) представлена в следующем виде:

n + 1     ,,n                          ,,n     ,,n                   Iiⁿ Iiⁿ

p ( X i , t n ) u = 1 1 a ( x_M, t ⁿ ) u - a ( X i , t ⁿ ) u^ 1 + f ( X i , t ⁿ ) ,

/ - 1, N - 1, u 0 - Ф 1 ( t n ) , u N - Ф 2 ( t n ) , u - v ( x i )

Коэффициенты a ( x_i , t ) определяются из выражения a ( x_i, t ) = 0,5 ( k ( x_i, t ) + k ( x_{i – 1} , t )).

Отсюда получаем явное выражение для нахождения u_i^{n + 1} на следующем шаге по времени.

Алгоритм схемы локальных итераций ЛИ-М подробно описан в работ ах [3; 5]. Алгоритм перехода от слоя tn к слою t n+ ¹ явно-итерационный. В цикле по l = 1,2 p - 1 вычисляется U :

u¹ = — {uⁿ + т bu' - 1 + t Lu' - 1 + t f ^{n +0}4

1 + t b l^V         '           h                ^;

Результат (2 p – 1)-ой итерации принимается в качестве функции на верхнем слое uⁿ + ¹ = U. Здесь Lh - диффузионный оператор; p = 0,25^ A t X _max + 1 - степень чебышевского многочлена; λ _max – значение верхней границы спектров дискретных операторов, отвечающих аппроксимациям процессов диссипативных членов. В соответствии с теоремой Гершгорина о кругах² величину Л max можно рассчитать, вычисляя для каждого узла сетки сумму модулей коэффициентов разностных аппроксимаций диссипативных членов. b_l – итерационные параметры, составленные особым образом из упорядоченного множества нулей многочлена Чебышева [1; 7].

Метод гиперболизации [3] основан на введении в параболическое уравнение второй производной по времени с малым параметром ω:

S u     S ² u S (      S и ^

р ( x ’ t Ь ^{+ Й}^Г⁼     k ( x ’ t )     ⁺ f ( x ’ t ) .

S t      S t² S x ^       S x J

Трехслойная разностная схема для этого уравнения строится следующим образом:

u n ^{+ 1}

—

2 т

u n ^{— 1}      u n ^{+ 1} — 2u n + u n ^{— 1}          1

-^ + W - i ----2---'— = -J---r

^{:                      т}               p ( X i , t n ) h

nn     n a (xi+„tn) u"/; — a (xi, tn) u-

V              ^h

—

h

n u—1

+ f ( X i , t n ) ,

где ω – малый параметр. Отсюда получаем явное выражение для нахождения u_i^{n+ 1} на следующем шаге по времени.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Проведено исследование трех вышеизложенных методов для решения следующего уравнения теплопроводности с переменными коэффициентами:

X u

Ht

ci (        си Л

= — ( e^x + 1 ) — + ( e dx ^        X .x)

■^x - 2 te^{2 x} -

u ( x ,0 ) = 0, u ( 0, t ) = t , u ( 1, t ) = te ¹.

Данное уравнение (2) имеет аналитическое решение:

u ( x , t ) = te^x .

Проводились расчеты на сетке с шагом h = 10^–3 м до времени T = 0,2 c.

Для явной схемы шаг по времени τ = 10^–7 с определен из условия устойчивости. Для схемы локальных итераций примем шаг интегрирования τ = 10^–3, для метода гиперболизации – τ = 10^–5 с.

• ²    Гантмахер Ф. Р. Теория матриц. М. : Наука, 1966. 576 с.

Technical sciences

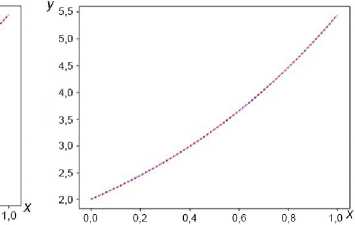
На рисунке представлены результаты расчетов по этим схемам и точное решение. Очевидно, все рассмотренные методы демонстрируют хорошую сходимость к точному решению. Для более детальной оценки порядка аппроксимации каждого метода вычислена средняя ошибка как норма разности между точным и приближенным решением.

Для оценки экспериментального порядка точности [8] по пространству были проведены расчеты на последовательности сгущающихся сеток h = 10^–3 м, h = 10^–3/2 м с сохранением числа Куранта. В результате для всех методов был получен порядок аппроксимации, равный 2, что соответствует теоретическому порядку аппроксимации каждой схемы.

Также были проведены замеры расчетного времени с заданными τ и h для каждого алгоритма (таблица).

В результате установлено, что схема гиперболизации показала наименьшее время расчета по сравнению с другими явными схемами.

• ^y    Л-------------------Л ^У5-⁵

  
  
  

• 5 .0                                     У5.0

• 4 ,5                          /4.5

• a)                                      b)c)

Р и с у н о к. Сравнение численных и аналитических решений: a) явная схема; b) метод локальных итераций; c) метод гиперболизации

F i g u r e. Comparison of numerical and analytical solutions:

• a) explicit scheme; b) local iteration method; c) hyperbolization method

Источник: составлено авторами.

Sources: compiled by the authors.

Т а б л и ц а. Анализ алгоритмов

T a b l e. Analysis of algorithms

Метод / Method	Явный / Explicit	ЛИ / LI	Гиперболизация / Hyperbolization
Отклонение между точным и приближенным решением / Deviation between the exact and approximate solution
Ошибка / Error	5,42846e-07	0,00155567	3,70791e-06
Порядок аппроксимации по пространству / The order of approximation
k	2,01954	1,90624	2,3244
Время выполнения алгоритмов, h = 10–3 м / The execution time of algorithms, h = 10–3 m
τ , с	10–7	10–3+173 итерации	10–5
Время, мс / Time, ms	65428	6654	1336

Источник: таблица составлена авторами на основе данных вычислительных экспериментов.

Sources: the table was compiled by the authors based on the data from computational experiments.

ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ

В работе реализованы численные схемы для решения уравнений параболического типа: широко известная явная схема, метод локальных итераций и метод гиперболизации. Численное исследование этих схем показало, что каждая из них имеет второй порядок аппроксимации по пространству. Однако расчетное время рассмотренной задачи у метода гиперболизации меньше. При решении систем уравнений параболического типа с применением явных схем метод гиперболизации позволяет существенно сократить время вычислений при сохранении требуемой точности.

Таким образом, исследование численных методов решения уравнений параболического типа является актуальной и важной задачей в области математики и информатики. Полученные результаты помогут сделать выбор наиболее подходящего алгоритма решения параболических уравнений при решении практических задач.