Исследование эффекта Баушингера и границы текучести при упругопластическом деформировании металлов

В теории пластичности тензоры напряжений и деформаций представляют [1-5] в виде

T o = ( с j = с о ( 5 j ) + ( S j) , Т_; = ( е j ) = е ₀( 5 j ) + ( Э у ), ( i , j = 1,2,3), (1)

где 5 j - символ Кронекера;

с о =а и /3, Е о = е п /3, ( i = 1,2,3)                 (2)

• -    средние напряжение и деформация (компоненты шаровых тензоров);

S j = с j - 5 j с о , Эу =е j - 5 j Е о , ( i , j = 1, 2,3)             (3)

• -    компоненты тензоров-девиаторов напряжений и деформаций соответственно.

Тензорам напряжений и деформаций (1) в линейном тензорнокоординатном евклидовом пространстве E 6 поставлены в соответствие векторы напряжений и деформаций [1-5]:

S = S0 + О, Ё = £0 + э, где

ё ⁰ _ с • ё-° _ гл • S ^_ S o i o, ^{£ _} ^ о i o

• -    векторы напряжений и деформаций объемного растяжения

и сжатия;

А    -- А

О = S k i k , э = Э k i k  ( k = 1,2,...5)                   (6)

векторы напряжений и деформаций формоизменения в пяти- мерном девиаторном подпространстве E5; |ik } - ортонормированный фиксированный базис А.А.Ильюшина тензорно-координатного подпространства E5;

<

S о = Ла ₀ , S = jlS_m S ₂ = -^-( S 22 - S зз ) , S з ='' S |₂ , S 4 = ■' S 23 , S 5 = ■' S ,3 ,

3 » =

1¹ - ^{3 2} = J- ( ^{3 22 - 3 33} ), ^{3 з} = Д > . , ^{3 4} = Д ^{3 23} . ³ 5 = Д ^{3 ,3}

• -    компоненты векторов напряжений и деформаций.

Модули векторов напряжений и деформаций в пятимерном подпространстве формоизменения E ₅ равны модулям тензоров-девиаторов:

°=V S ^ S T= _х^ , 3 = 33 = 33 , ( k = l,2,...5), ( i , j = l, 2,3).

В теории пластического течения вводятся две основополагающие гипотезы [3, 6]. Первая гипотеза состоит в разложении тензора-девиатора деформаций на упругие е j и пластические £ Р части, что позволяет ввести понятие о мгновенной гипотетической поверхности текучести f ( о , Э^р ) = 0, разделяющей в подпространстве формоизменения E ₅ область активного пластического деформирования и область упругой разгрузки [3, 6] (рис. I). Принцип градиентальности Драккера позволяет определить приращения векторов упругих и пластических деформаций [6] для активного и пассивного процессов деформирования соответственно.

= 7°, dЭ^p = d X grad f ,( do • grad f >  0),

• 2 G

• = d° , dЭ^p = 0, ( do • grad f <  0).

2 G

/^{Э е} dЭ ^e

Вторая гипотеза относится к возможности разложения полного вектора напряжений (рис. I) [6-8]:

о = о 0 + a ,                           (io)

где о 0 - вектор активных напряжений; a - вектор добавочных остаточных микронапряжений в E ₅.

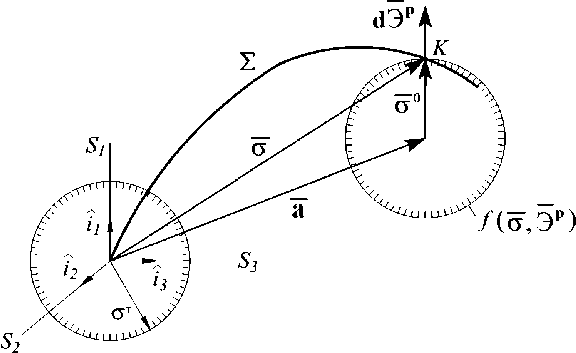
Рис. 1. Разложение полного вектора напряжений в E 5

Математические модели (определяющие соотношения) теории течения отличаются формой поверхности текучести. В наиболее распространенном на практике варианте теории с трансляционно-изотропным упрочнением материала она имеет форму сферы:

2 f = О ⁰ • О ⁰ - C p ( s^p ) = 0, (11)

которая может изменять свои размеры и местоположение [6-8]. Здесь а0 = Cp (sp) - скалярная функция изотропного упрочнения, равная радиусу поверхности текучести; sp - длина дуги траектории пластического деформирования. В начальном состоянии при sp = 0 радиус гипотетической начальной поверхности текучести а0 = а1 = V2/3а т (см. рис. 1), где ат - начальный предел текучести при простом нагружении, определяемый по техническому допуску на остаточную деформацию Эр « 3/2 еЦ = 0,245 % (ep = 0,2 %). Принимается универсальный закон упрочнения Одквиста-Ильюшина а = Ф( s), (12) мало отличающийся от закона единой кривой при простом нагружении а = Ф(Э). За новый предел текучести принимается точка K начала разгрузки (12).

Эффект Баушингера при знакопеременном нагружении в E ₅ оценивается [9] безразмерным параметром

7 = |^а М |/ ^а К                           (13)

при соответствующей величине дуги траектории пластического деформирования s^p , где а К - новый предел текучести на диаграмме растяжения в некоторой точке К начала разгрузки; а^Т_М - вторичный предел текучести при разгрузке из той же точки К при «протыкании» поверхности текучести по диаметральному направлению в результате излома траектории на 180° в E 5 , определяемый по допуску на остаточную деформацию Э*⁷. Радиус а ⁰ = C_p гипотетической текущей сферической поверхности текучести, изменяющийся в результате пластического деформирования [3, 10] при условии сохранения ее формы

_ т т 0      аК аМ а = Cp = —2—,               (14)

а смещение ее центра т т     _а К + а М a = ак -Cp = —2—•              (15)

Экспериментальное исследование функций а0 = Cp (sp) и a(sp) проводилось в опыте при знакопеременном нагружении-разгужении на автоматизированном испытательном комплексе на сложное нагружение CH-ЭВМ им. А.А.Ильюшина в лаборатории механических испытаний кафедры «Сопротивление материалов, теория упругости и пластичности» Тверского государственного технического университета. В опыте использовался тонкостенный трубчатый образец из стали 45 в состоянии поставки с площадкой текучести, который имел толщину стенки h = 1 мм, радиус срединной поверхности поперечного сечения R = 15,5 мм и длину рабочей части l = 110 мм. В результате испытания образец подвергался многократному знакопеременному нагружению через равные приращения АЭ, = 0,5 % при растяжении (рис. 2, 3), с последующим знакопеременным нагружением на |АЭ| ~ 0,75 - 0,9% при сжатии. Опыт в режиме непрерывного деформирования продолжался в течение 8 часов. На рис. 4 представлены полученные опытные зависимости параметра у от длины дуги траектории пластического деформирования sp, характеризующие эффект Баушингера, на рис. 5 - изменение радиуса а0 гипотетической сферической поверхности текучести, а на рис. 6 - график смещения центра гипотетической сферической поверхности текучести в зависимости от параметра sp. Все представленные зависимости построены при различных допусках на остаточную деформацию в*7 = 0,2; 0,1; 0,05; 0,025%, что в E5 составляет Эр = 0,2 45; 0,1225; 0,06125; 0,030625% соответственно.

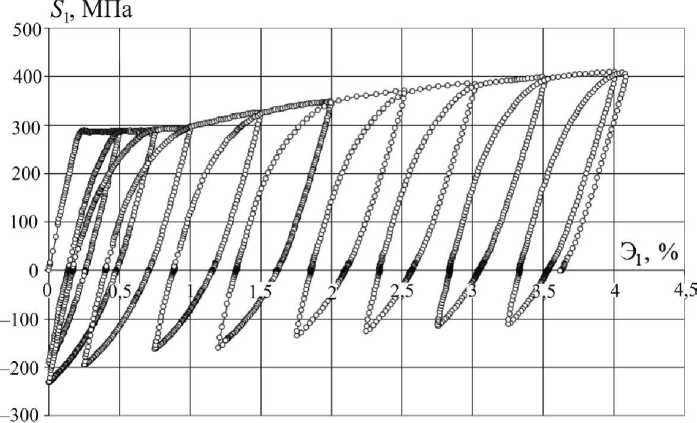
Рис. 2. Локальная диаграмма знакопеременного нагружения S 1 - Э 1

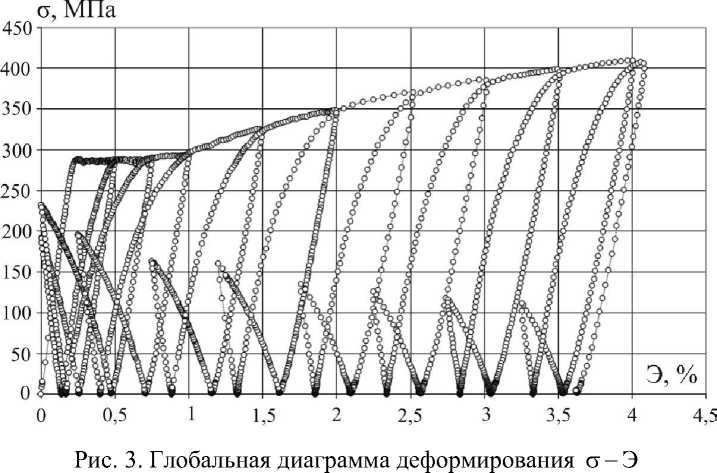
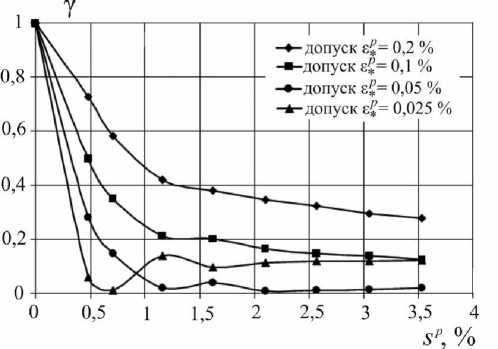
Рис. 4. Эффект относительного изменения предела текучести по Баушингеру

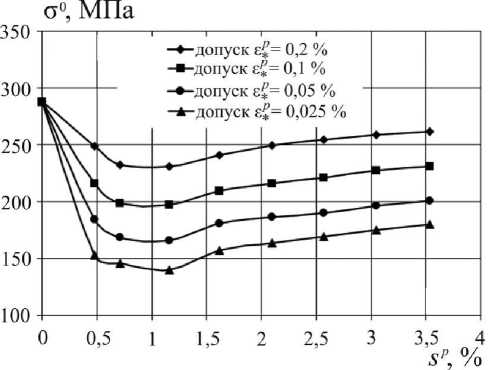
Рис. 5. Изменение радиуса гипотетической поверхности текучести

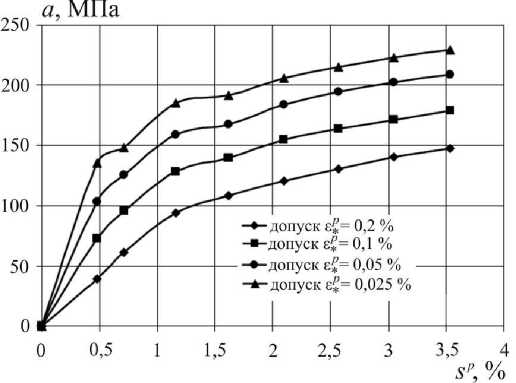
Рис. 6. Смещение центра гипотетической поверхности текучести

С ростом допуска на остаточную деформацию радиус поверхно- 0

сти текучести о увеличивается, а смещение ее центра а уменьшается. Максимальное отклонение для рассмотренных крайних допусков на остаточную деформацию а*⁷ = 0,2% и а*⁷ = 0,025% для радиуса о ⁰ гипотетической поверхности текучести составляет примерно 45 % (см. рис. 5), а для смещения ее центра - примерно 55 % (см. рис. 6). При максимально достигнутом уровне пластической деформации s^p значения параметра а при различных допусках на остаточную деформацию не превысили значения начальных пределов текучести о ¹ , следовательно, центр текущей поверхности находится внутри начальной поверхности текучести.

За технический предел текучести о _т в теории пластичности принимается такое напряжение при растяжении, при котором остаточные деформации становятся одного порядка с упругими ( а « 10 ^{— 3}). За такую остаточную деформацию, как правило, принимают а*⁷ = 0,2% = 2 - 10 ^{— 3} (Э*⁷ = 0,245 %). Начальная поверхность текучести в девиаторном пространстве А.А. Ильюшина при данном допуске на остаточную деформацию описывается сферой Мизеса для начально изотропных тел. При меньших допусках очертание сферы Мизеса искажается и теряет свою форму [8]. На девиаторной плоскости окружность Мизеса и вписанный в нее шестиугольник Сен-Венана приобретают тройную симметрию [11]. При этом начальные условия текучести Мизеса и Сен-Венана определяются формулами [3-5]

• ^{1                2              2              2}     _т

°=-R^°1    ) +(°2— о3 ) +(°3-°1) =о ,

³                                                       (16)

С™ — о,,

Tmax =---2---= k (m < n’ m, n = 1,2,3), где оi (i = 1, 2, 3) - главные нормальные напряжения; k - предел текучести при плоском чистом сдвиге. Уже при а*7 = 0,1% классическая теория пластичности лежит за пределами ее инженерного контроля [3, 6, 8]. К сожалению, в некоторых математических моделях теории течения величине допуска на остаточную деформацию не придают значения и не связывают их с определением предела текучести. В про- цессе нагружения при трансляции предельной поверхности она вытягивается в направлении развития процесса вследствие развития деформационной анизотропии [3, 6].

По результатам экспериментально проведенного исследования можно сделать выводы.

• 1.    Эффект Баушингера для стали 45 с площадкой выражается уменьшением по модулю вторичного предела текучести с _м и параметра у с ростом длины дуги пластического деформирования s^p . Параметр у при различных допусках на остаточную деформацию стремится к некоторому стационарному значению при s^p >  3 %.

• 2.    С ростом допуска на остаточную деформацию Э^р параметр у увеличивается и при максимально достигнутом значении s^p для общепринятого допуска е * = 0,2% (Э ^р = 0,245%) составляет примерно 0,3.

• 3.    Радиус гипотетической сферической поверхности с ⁰ = C_p ( s^p ) совершает временное понижение типа «нырка», а затем увеличивается. При повышении допуска Э^р примерно до технического и более очертание поверхности стремится к сферической. При этом отклонение радиуса при крайних значениях допуска на остаточную деформацию достигает 45 %.

• 4.    Отклонения параметра смещения центра предельной поверхности a ( s^p ) для рассмотренных различных допусков на остаточную деформацию при определении пределов текучести достигают 55 %.

• 5.    В некоторых математических моделях теории течения временное убывание функции с ⁰ = C_p ( s^p ) в начале процесса пластического деформирования не связывают с определением пределов текучести по допуску на остаточные деформации и искажением гипотетической сферической поверхности текучести, что абсолютно нереально и не вызывает доверия к ним.