Исследование эффективности и динамики проектно-производственных процессов в авиастроении

Каждый ТП можно охарактеризовать набором приписываемых ему структурных компонентов для моделирования текущего режима, а также весовы-ми характеристиками относительной важности этих компонентов в множестве структур моделей, например , в виде ориентированного графа производственной системы при расчете текущего режима функционирования.

Задача может быть решена в рамках предлагаемого способа формального выбора требуемого подмножества из фиксированного множества допустимых вариантов.

Пусть задано конечное множество структурных компонентов D={D_l,...,D_m}, i=l,m, включающее непересекающиеся подмножества D_i={d_i1,...,d_ik}, конечное множество режимов a _icj=j(d_ic,l_j), i = 1,m, j = 1,n, с = 1,k, трактуются как значения с-го элемента структурного компонента D_i вектор-строки в режиме функционирования l_j, представленном вектор-столбцом. Каждому элементу подмножества D_iмножества структурных компонентов D приписывается весовая оценка ω⁰_ic, ω⁰_i=(ω⁰_i1,…,ω⁰_ik), определяющая важность элемента d_ik для формирования структуры модели ТС.

Пусть Iⁱ_j — столбец с номером j матрицы А⁽ⁱ⁾. Выделим в матрице А⁽ⁱ⁾ какие-либо b строк и пусть множество M^b_ij — логически упорядоченный набор из b элементов а_ibj матрицы А⁽ⁱ⁾, стоящих на пересечении каждой из выбранных строк с j-м столбцом M^b_ij={a_i1j,…,a_ibj}, bкции F^b_ij(M^b_ij), которые определены для всех j= 1,n на всевозможных упорядоченных наборах М^b_ij элементов, дают интегральную оценку b-го варианта i-го структурного компонента.

Следовательно, область определения M^b_ij,– наборы значений подмножеств подмножества структурных компонентов D_i на l_j, а F^b_ij — оценка этих наборов. Следовательно, индекс b в функции F^b_ij будет определять количество возможных вариантов набора элементов (подмножеств) для каждого подмножества D_i структурных компонентов при l j .

Функции F^b_ij будем считать монотонными: с увеличением мощности подмножеств значение F ^b_ij не убывает. Определены и имеются наборы чисел P_ij, i=1,m, j=1,n, используемые при задании ограничений снизу на значения F^b_ij, а также заданы числа X icr , c=r, i=1,m, c,r=1,k, характеризующие возможную корреляцию между отдельными элементами в подмножествах D_i при l_j.

Из множества D структурных компонентов для каждого подмножества Di при lj из b вариантов необходимо выбрать подмножество Sopij ={di1j,…,dibj} таким образом, чтобы была удовлетворена система неравенств вида mxFbj (Mj) = minFbj (^(dj,-,^(dblj^P i = 1, m , j = 1, n

Такой подход позволяет показатели оптимальности Рij интерпретировать как уровни обеспечения значений критериев оптимизации для заданных условий разработки проекта технологической системы. Каждой из поставленных целей соответствует своя функция Fbij и свой уровень критериев Рij. Чем ниже уровень критериев, тем с меньшими затратами средств дос-тигается реализация проекта при определенных условиях производства.

Сложность любой системы обусловлена числом ее компонент и способом их взаимосвязи. Такая сложность относится к реализации системы. Исходя из вышеприведенных рассуждений, определим ТС как множество разнородных взаимодействующих единиц, в число которых включены проектная Х и производственная Y системы, образующие динамическую систему, описываемую двумя связанными автономными нелинейными уравнениями (автономность означает, что время не входит в качестве свободного параметра):

= f , ( X , Y , m )            (1)

— - f _г ( X , Y , m )           (2)

Система эволюционирует в двухмерном пространстве состояний переменных Х, Y. В каждой точке траектории, заданной выбором конкрет- ных начальных условий Х(0)=Х10, Y(0)= Y10, наклон определяется величиной dY = A dX f, .

Особые точки (стационарное состояние) на траектории – это точки, в которых f2=0 и f1=0, т.е. не определена касательная. С другой стороны, замкнутые траектории, соответствующие периодическому режиму, имеют основной период, определяемый по формуле

T _{= (}f--- dX---

J f ,( X , Y , m ) .

Исследуем устойчивость стационарных состояний, вводя малые возмущения х(t) от положения равновесия, а именно возмущения, удовлетворяющие ограничениям x(t) = X - X(t)| << E y(t) = Y - Y(t )| << v где e, v - положительные числа, задаваемые исходя из обеспечения стационарного режима.

Для данного стационарного состояния мы разлагаем правые нелинейные части динамических уравнений в ряд Тейлора относительно стационарного значения отдельной переменной и, если функции fi достаточно гладкие, удерживаем в разложении только линейные члены.

Мы получаем:

dx ( t ) dt

dy ( t ) dt

= ( X - X *) \ ^df^Y |

^uw у X = X *

= (Y - Y4^f I

ay

/ Y = Y *

(свободный член разложения Тейлора равен нулю). f( X *, Y *, m) = 0, dX *

так как dt

= 0 и

dY * dt

= 0 .

На функциональном уровне сложность определяется многообразием технологических действий в системе.

Рассмотрим задачу проектирования производственных процессов, связанной с необходимостью определения степени приоритетов весовых коэффициентов потоков в дугах графа системы как модели по условиям качества выполняемых сборочных операций. Например, трудоемкость сборочных операций Х или реализации сборочных процессов в систему поступают различные ресурсы D от управляющей структуры Х. Производственная система Y полученные ресурсы от Х преобразует на производстве в реальные агрегаты самолета. Следовательно, производственная структура Y должна обладать такими свойствами, которые обеспечивают выполнение проектных решений ТС с заданными показателями эффективности и качества. Для обеспечения жизнедеятельности в нее поступают денежные средства D финансово-кредитных структур, которые суммируясь с оборотными фондами и оборотными средствами проектной структуры Х, увеличивают сумму денежных средств этой структуры (Х растет на D). Производственная структура Y получает средства от Х на постановку производства изделий (авиационной техники). Наконец, производственная структура Y, вступая в контакт с рынком авиационной техники (заказы – денежные средства на производство изделий В) создает эту технику (рис. 1).

Такая схема применима к процессам производства в условиях возможной неоднозначности производственной ситуации.

Обозначим переменные состояния Хi и Yi при zi, zj через

^f- )

I a z, \    .• ,            (7)

V j 7 Z=Zj где bij – параметр, характеризующий взаимодействие и описывающий степень воздействия переменной Хi на переменную Yj , причем в общем случае bij= bji. Равенство bij =0 может указывать на отсутствие переменной Хi в многочлене fi. Элементы bij образуют так называемую матрицу взаимодействия В.

Линеаризованная система дифференциальных уравнений с возмущениями хi (t) в качестве неизвестных функций имеет теперь вид dzi N

§ (8)

или x=Ax.

Выбирая возмущения Х; ( t ) ~ e ^X t , получаем линейную систему

N

Xz = У bnz i ii           ij  j j=1

или в матричной форме Xz = Az.

Требование нетривиальности решений [zi(t) ?0] приводит в нашем случае к характеристическому уравнению

b11 - X b12 = 0 b21 b22 - X (10) или

(b_u-X) • (b 22 -X) - b₁₂^b 2! = 0;           (11)

X² - (b_n b 22 ) • X + (b^- b i2 ^b 2i ) = 0, (12)

которое можно представить в виде

X ² - k X + у = 0 .           (13)

В общем случае мы получим X12 = (X’+j X’’).

Возникающее стационарное состояние неустойчиво, если Re{ лi}<0 при i =1 и i=2. Если X’1= X’2=0 и X’’=0, мы имеем режим на границе области устойчивости, или нейтральную устойчивость; иначе говоря, система совершает периодическое движение с частотой X’’ по замкнутой траектории вокруг стационарного состояния, причем радиус траектории может быть малым но зависящим от начальных и граничных условий. Число возможных состояний системы может достаточно большим для всех возможных случаев в зависимости от параметров k и у, поэтому проведем исследование реальной системы (рис. 1)

Функционирование должно протекать следующим образом:

D + X —mX ,(14)

X + Y " >nY,(15)

X + B —k3^ C + B,(16)

где k1, k2, k3 – константы скоростей реализации проектов.

Соответствующие дифференциальные уравнения относительно Х и Y могут быть выведены непосредственно на основе подсчета приращений и убылей материально-финансовых средств и числа реализованных проектов. Например, Х возрастает со скоростью k1DX и убывает со скоростью k2XY, поэтому dX

— = kDX - k.XY

.

С другой стороны, Y возрастает со скоростью k2XY и убывает со скоростью k2BY, поэтому

— = k.XY - k.BY dt 2           3       .

Нелинейные правые части – многочлены – имеют вид:

f1 = k1DX – k2XY и f2 = k2XY – k3BY.

Параметры k1, k2, k3, D, B являются управляющими параметрами, заменяющими в формальных

Восстановление ресурсов

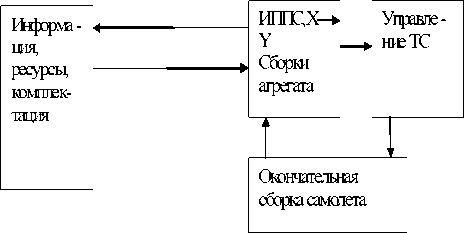
Рис. 1. Схема взаимодействия ТС сборки агрегата с ИППС уравнениях динамической системы - параметр р.

Определим стационарные состояния. Решая систему уравнений f1=0, f2=0, мы находим два вещественных решения

Стационарное состояние II. Производя анализ, аналогичный проделанному выше, но вычисляя теперь значения производных в точке Х^*₁₁ =0, Y^*₁₁ =0, получаем

X, * = К з В

'       K 2 ,

Y * = ^K ' D '       K 2 ^,

b" = K ' A    b '₂ = 0

b 21 = 0    b ₂₂ = - K ₃ B

X _п* = 0 , Y _n* = 0 .         (20)

которые представлены на рис. 2.

Исследуем каждое из них на устойчивость.

КОНКРЕТНЫЙ АНАЛИЗ ТЕХНОЛОГИЧЕСКИХ ПРЕОБРАЗОВНИЙ В ОПЕРАЦИЯХ СБОРКИ

Стационарное состояние I. Требуется вычислить собственные значения матрицы В линеаризованной системы, что сводится к вычислению коэффициентов b_ij. Получаем

Характеристическое уравнение в этом случае имеет вид

(K 1 D - X)- (K 3 B + X)=0 (24) и собственные значения оказываются равными X 1 = K 1 D >0 и X 2 = - K 3 B <0.

Стационарное состояние (0,0) неустойчиво.

Так как рассматриваемая система функционирует в пространстве состояний переменных Х,Y, то замкнутые траектории, соответствующие периодическому режиму, имеют основной период, определяемый по формуле

b ''

b 2'

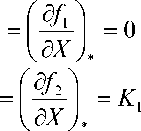
b '2

b 22

5 f . ) a y ) * (f' Id Y

= K ₃ B

T _f

dX

f ( X , Y , k ' , k 2 , k 3 , A , B ) .

= 0

*

где звездочка означает, что численные значения производных следует брать при

KB KD

X * = —³—   y * = —'—

'      K ₂ ,     ' K ₂

Из характеристического уравнения (13) находим

X = ±V K ' K ₃ DB .         (22)

Это означает, что стационарное состояние 1 нейтрально устойчиво и, когда система под действием слабого возмущения покидает это состояние, она переходит на периодическую траекторию, размеры которой определяются величиной возмущения, и описывает ее с циклической частотой, равной X = ± д/ K ' K ₃ DB (двигаясьв про-

странстве состояний, где значения переменных растут от начала, всегда по часовой стрелке).

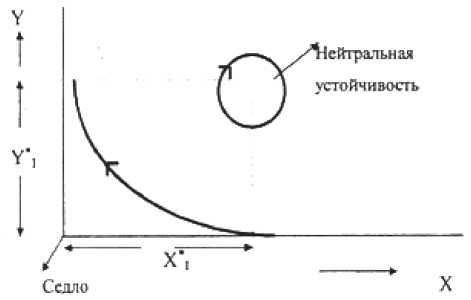
Рис. 2. Устойчивые режимы модели ИППС

При этом k1, k2, k3, D, B учитывают скорости протекания реальных процессов в системе и показатели, характеризующие систему, которые разбиваются в нашей системе на два уровня (проектный и производственный).

Отметим, что одним из эффективных методов в исследовании многокомпонентных производственных систем является интегральный метод в решении задач факторного анализа.

Развитие интегрированных проектно-производственных систем (ИППС) при разработке ТС представляет собой многофакторный процесс. В то же время организационная структура производственной системы, представляющая собой сложноорганизованную иерархию, определяет свойства функциональных элементов, упорядоченным образом связанных друг с другом , а изучение соотношений между этими элементами, составляет основу исследования операций.

Например, если Q является семейством всех независимых множеств графа G, то число a [G ] = max |S | является числом S e Q независимости графа G, а множество Si , на котором этот максимум достигается, становится наибольшим независимым множеством.

Такие соотношения подмножеств графа системы должны поддерживаться моделями проверок системы при неизвестном распределении времени ее безотказной работы . Известно только значение Р – квантиля t_p функции F(F _(tp) = P) , а также максимально возможное время работы системы F. Предположим, что мы исследуем фактор – интенсивность отказов:

X (u) = [ F(u + A ) - F(u) ] /G(u) , где

G(u)-1 - F(u), u >  0, A >  0 - неубывающая функция, найдем минимальную стратегию проверок Р’’ такую что

L'' = L(P' ',F'') = min L(P, F'') = min max L(P, F), P                PF где L – функция издержек, трудоемкости процесса. Считаем что проверки в автоматизированных линиях сборки мгновенны, а проверка в момент Т обязательна. Если отказ прозошел до момента Т, то издержки равны C+Rt, т - время от момента отказа до его обнаружения.

Стратегию проверок ищем в виде

P {0 т < .„• t, -Т}, где ti (i=1, …,N; i=m+1) – моменты проверок, а в моменты tm+1=tp проверка может не проводиться. Предположение о том, что А=1, Т=1 не ограничивает общности решения. А – стоимость одной проверки.

Также имеем в этом случае:

n-1                  n

L = A ^ G(t , ) +R £ G(t , )(t , + i -t_l)- J G(t)• d(t)

1=0                  l=00

l^m+1l

+ C • F(T).

При этом оптимальная стратегия от С – сложности компонент ТС не зависит. Следовательно, в результате практического решения такой задачи факторного анализ можно выделить три основных подхода к задаче повышения устойчивости и надежности ТС:

• 1)    Физический – внедрение более совершенных с большим средним временем безотказной работы компонент системы;

• 2)    Структурный – разработка методов и способов синтеза системы ТП и алгоритмов ее функционирования, в сочетании с требуемым техническими средствами;

• 3)    Функциональный – проектирование эффективной системы управления с учетом реальной производственной среды.

Решение задачи представим также примерами компоновки системы с точки зрения структуры и ее функций в виде двух схем (рис. 3):

Соответственно надежность определяется:

Ra=A1 A2(2 – A1)(2 - A2); Rb =A1 A2(2 – A1 A2).

Тогда надежности двух схем при нагруженном резерве выражаются через надежность элементов

A₁ иA₂ , где A₁ и A₂ – функции времени, а из неравенства (1 - A 1 )( 1 - A 2 ) > 0 получим, R a > R₆, где равенство возможно только при абсолютной надежности компонент ТС.

Следовательно, в графе системы сборки вводится два или более вариантов весов качества системы ТП, а плотность соответствующего подграфа определяется как фактическое максимальное число вершин графа. Тогда кликовое число графа как плотность вероятности состояния ТС в производственном потоке определяется степенью связности его вершин. Для снижения объема вычислений в этом случае применим систематический метод перебора, снижающий объем вычислении, и не требующий запоминания генерируемых независимых соответствует максимальной связанности его вершин. С другой стороны, степень независимости системы снижается в связи с увеличением числа компонент, обеспечивающих высокую функциональность и качество ТС. В целом при нахождении всех максимальных независимых множеств графа по исследуемым факторам с наибольшим числом вершин (порядка 20) предлагается использование метода последовательного перебора независимых множеств с одновременной проверкой каждого множества на максимальность значения исследуемого фактора путем добавления к исследуемому множеству дополнительной, не принадлежащей ему вершины и выяснения условий сохранения независимости с последующим запоминанием текущих максимальных множеств., полученных ранее, и становятся не максимальными на данном этапе решения. множеств с целью проверки их на максимальность ,допустим, способом сравнения с ранее сформулированными множествами.

Предлагаемый подход позволяет определить методику обеспечения устойчивости системы сборки по доминирующим критериям оптимизации производственных схем с учетом требований по качеству сборок и ритмичности поставок комплектующих. Для практического применения методики применимы соответствующие алгоритмы:

• -    алгоритм решения задач об оптимальном начальном запасе и графиках поставок по критерию минимума среднего запаса;

  (a)

  

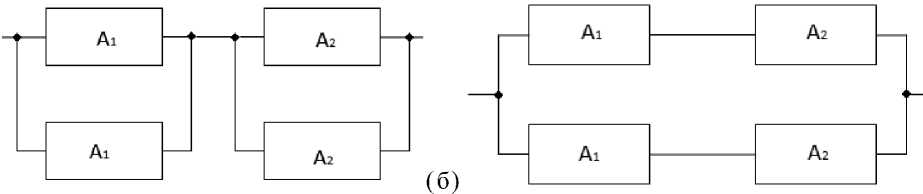
  Рис. 3. Две схемы структурных соединений компонент рабочих мест исполнителей

  
  

• -    алгоритм определения практического приближения к оптимальному управлению по математическому моделированию и способами управления технологическими системами.

Проблема управления системой сборки в данной постановке занимает важное место в теории автоматического управления процессами на производстве. Она обеспечивает реализацию концепции упреждающего управления ,которая основана на том, что значение управления в текущий момент времени t менее подвержено действию различного рода возмущений, если найдено с учетом знания будущего поведения системы на интервале времени ( t, t + h ) длины h >  0. Применительно к дискретной системе с интервальными коэффициентами концепция требует прогнозирования состояния сборочного пространства на несколько тактов времени вперед, т.е. представления его в виде линейной комбинации неопределенных векторов. Если потребовать, чтобы линейная комбинация совпадала с положением равновесия, то естественно приходим к необходимости решения линейного алгебраического уравнения с интервальными оценками коэффициентов. В данном случае используется понятие частного решения в пределах возможности универсальных решений интервальных задач. Оно позволяет найти стабилизирующее управление в виде линейной функции текущих координат потоков сборки, оценить степень близости решения дискретной системы к положению равновесия, получить условия на интервальные коэффициенты, гарантиру-ющие притяжение траекторий замкнутой системы к положению равновесия.

ЗАКЛЮЧЕНИЕ

Предлагаемая методика выбора модели ТС, методов ее оптимизации и определение стационарных устойчивых состояний позволяет при удовлетворении заданным и начальным граничным условиям вычислять такие параметры производственных процессов, которые соответствуют устойчивости функционирования агрегатносборочного производства. Обеспечивается также возможность мониторинга сборочного производства в непрерывном режиме. Предлагаемая методика расчета параметров устойчивости и стационарности системы позволяет в процессе проектирования операций сборки прогнозировать возможные критические состояния производства с большой вероятностью роста интенсивности отклонений. Способ выбора моделей ТС с введением и ранжированием весовых характеристик дуг графа как моделей общей системы позволяет проводить необходимую в производственных условиях работу по перераспределению потоков в системе для обеспечения устойчивых состояний отдельных рабочих мест исполнителей в допустимых режимах работы, освоения других изделий и более совершенных технологий, например, GPPM. Предлагаемый подход связан с решением задач контроля сборочных процессов и получения количественных и качественных оценок их эффективности. В этом случае обеспечивается планомерное наращивание показателя прироста качества и стоимости создаваемого изделия при расходе некоторых ограниченных ресурсов. Установлены основные предпосылки обеспечения устойчивости ТС, базирующиеся на аппарате математического моделирования и решения адекватных систем линейных и дифференциальных уравнений, что позволяет представлять текущую информацию в общей информационной системе предприятия в цифровом виде для обработке в автоматизированной системе проектирования и управления производством.