Исследование эффективности парадигмы факторной оценки знаний на примере тестирования студентов по теории автоматического управления
Автор: Нейдорф Рудольф Анатольевич, Обухова Елена Николаевна
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 3 (82) т.15, 2015 года.
Бесплатный доступ
Разработаны актуальный алгоритм построения тестовых материалов и методика оценивания результатов тестирования, позволяющие сочетать высокую оценочную способность и объективность тестов. Тестовую систему в таком случае можно рассматривать как аппарат оценивания уровня знаний при изучении соответствующих модулей. Для систематизации знаний производится декомпозиция знаний на множество разделов. При этом каждому разделу сопоставляется множество подразделов, которое, в свою очередь, состоит из подмножества вопросов, ответы на которые раскрывают уровень знаний каждого раздела. Задание теста формулируется таким образом, что при ответе на него должен быть дан набор ответов, раскрывающих уровень знания определенного подраздела. Поскольку процесс разработки тестового вопроса рассматривается как построение многофакторной зависимости, то предлагается к его построению подойти с позиции планирования многофакторных экспериментов. В этом случае множество ответов представляется как набор факторов, принимающих определенные значения. При их варьировании на двух уровнях, задача сводится к построению эксперимента, реализующего все возможные сочетания факторов, т.е. к полному факторному эксперименту. Предложена методика применения технологии планирования двухуровневых многофакторных экспериментов, позволяющих формализовать оценку частично неполных знаний и реализацию формирования многофакторных тестов различной сложности. Для иллюстрации данной методики рассмотрены примеры построения тестов для дисциплины «Теория автоматического управления», оценивающих степень сформированности уровня знаний. Статистическая обработка результатов тестирования показала уровень знаний испытуемых, а также степень доверия к этим знаниям.
Тестирование, фактор знания, тестовый вопрос, оценка ответа, вариативность ответа, неравномерность знаний
Короткий адрес: https://sciup.org/14250156
IDR: 14250156 | УДК: 517.977:62 | DOI: 10.12737/12596
Текст научной статьи Исследование эффективности парадигмы факторной оценки знаний на примере тестирования студентов по теории автоматического управления
Введение. Проблема оценки и аттестации знаний студентов в условиях введения новых федеральных государственных образовательных стандартов является актуальной для всех российских ВУЗов. Особое внимание уделяется подходам и методам, позволяющим повысить эффективность использования имеющихся средств контроля знаний в условиях ограниченности материальных ресурсов [1–4].
Удобным и эффективным средством контроля знаний является тестирование [1, 2]. Несмотря на то, что тестовый контроль является одним из перспективных методов оценки знаний и определения уровня подготовки обучаемых, существует множество проблем, с которыми сталкивается преподаватель при внедрении его в учебный процесс. Эти проблемы связаны как с подготовкой тестов, так и с оценкой результатов тестирования [5, 6].
Одна из проблем связана со сложностью задачи составления тестов и создания достаточно развитых баз тестовых заданий по учебным дисциплинам. Это, конечно же, требует не только больших трудозатрат преподавателей, но и, в первую очередь, конкретной, доступной, и, желательно, универсальной методики построения тестов. Кроме того, желательно, чтобы эта методика была поддержана необходимым алгоритмическим и программным обеспечением с развитым, удобным и легко расширяемым интерфейсом [7–10].
Кроме этого, проблемой внедрения тестирования является ограниченность возможностей существующих тестовых технологий. Это относится и к целенаправленному формированию функционала и структуры тестов, и к оценке качественной составляющей знаний студентов, а также к процессу проверки и обработки результатов тестирования [11, 12].
Под качественной составляющей тестового задания здесь понимается возможность оценить степень усвоения учебного материала через выставляемую в виде балла оценку.
В частности, возможности теста расширяются, если используется несколько допустимых ответов с разной степенью достоверности ответа. Тогда, даже в случае дозволенности одного ответа на вопрос, тестируемый будет иметь оценку, выраженной долей полного знания [13]. Недостатком такого подхода является то, что он не защищен от угадывания правильного ответа. Тестируемый в этом случае, имея даже приблизительные знания о вопросе, с большой вероятностью имеет шанс угадать ответ с достаточно высокой оценкой. При этом невозможна оценка достоверности результата тестирования.
Эту проблему частично решают системы тестирования, допускающие выбор нескольких ответов, кажущихся тестируемому наиболее близкими к истине. Тогда возникает возможность оценить и уровень знаний, и степень их «размытости».
Общая характеристика проблемы. В работах авторов [14, 15] предложен и в значительной степени развит подход к описанной проблеме, а также даны различные частные примеры ее решения. В данном подходе авторы исходят из того, что основным постулатом тестирования является наличие вычлененного из изучаемого материала множества
Q = { qi\i = 1 -n\ (1)
вопросов q i , отражающих в совокупности его знание. Степень знания обучающимся вопроса q i считается в процессе тестирования «фактором знания» (ФЗ) и обозначается x i . Таким образом, тестирование превращается в факторный эксперимент, задача которого дать общую оценку совокупности знаний обучающимся изучаемого материала.
Факт знания тестируемого учебного материала отображается отношением
^•^ ( q k ) ^ a k е A = V*klk = 1 .-•» } , (2)
Где A t — множество правильных ответов a‘k на вопросы qk е Q в (1).
Естественно, факт незнания некоторых элементов изучаемого материала отображается отношением
S.'S ( q l ) ^ a { е A f = { a lf |l = 1 ,..n } , (3) Где Af — множество неправильных ответов a { на вопросы q l е Q в (1).
Вполне очевидно, что формулировки как правильного, так и неправильного ответа можно сформулировать различным образом. Это зависит от особенностей языковой среды, используемых для раскрытия знания исходных материалов (монографий, учебников), особенностей терминологии их авторов, субъективных особенностей преподавателя, разрабатывающего текст, и многого другого. Однако будем считать, что в конкретной образовательной среде сформированы свои конкретные q k , q l , a kt и a lf . Тогда ответ на вопрос по ФЗ можно считать абсолютной оценкой этого элемента знания.
Следовательно, мы имеем факт двоичной оценки ФЗ: «знает — не знает». Такой структуре теста соответствует двухбалльная оценка знаний: «0 – 1». Однако степень подготовленности тестируемого определяется совокупным множеством ответов на множество вопросов, оформленных на основе выделенных ФЗ изученного материала. Таким образом, степень знания одного вопроса тоже может быть разной и оценивать общую картину знания обучаемого сле-
Информатика, вычислительная техника и управление
дует по доле правильных ответов в полном множестве (1). Но тест, оформленный как последовательный процесс ответов по всем ФЗ даже небольшого раздела дисциплины получается слишком громоздким и утомительным.
В тестах, учитывающих этот фактор, множество Q целесообразно разбивать на подмножества Q i , причем
П Q i = Q, , (4)
где каждое подмножество Q i представляет собой отдельный тестовый вопрос (ТВ), содержащий некоторое количество ФЗ, объединенное общей смысловой направленностью [16, 17].
Для выявления уровня знания каждого вопроса Q i ему сопоставляется подмножество ответов A i , причем
A^A , |П A , = (A i , A f ) } , (5)
т.е. в множестве A i ответов, предлагаемых на вопрос Q i должны обязательно содержаться ответы содержащие все правильные (2) и все неправильные (3) ответы по ФЗ. В противном случае тест приобретает характер либо провокации, либо подсказки.
Остальные варианты ответов A ij в (5) могут содержать некоторую долю неправильных ответов a ijf согласно (3). Если условная доля содержания правильной информации в таком ответе определена, то таким ответам можно сопоставить различные баллы, по которым можно оценивать степень знания вопроса. Комбинируя множества таких ответов можно составлять тесты, которыми можно оценивать «палитру» знаний [16, 17]. Условие (4) при этом обеспечивает совокупную оценку всего знания представленного множеством Q в (1).
Однако необходимо учесть еще один недостаток, свойственный традиционной структуре процесса тестирования. Выбор единственного ответа на тестовый вопрос значительно снижает эффективность даже предложенного выше усовершенствованного подхода к тестированию, т.к. при неполном знании возникает возможность проявления стойких эффектов, как угадывания, так и невезения. В работах [13–17] авторами предложен кардинально отличный подход — дать испытуемому возможность выбора нескольких вариантов ответов, которые на его взгляд кажутся наиболее близкими к правильным, не исключая права тестируемого выбрать один вариант ответа. Последнее характеризует уверенность его знания и соответствует выбору одного и того же ответа несколько раз.
Пример решения задачи тестирования знаний на основе парадигмы их факторной оценки. В работах [13–19] проанализированы возможности изложенного выше подхода и проверен ряд его положений. Практика использования факторных тестов показала, что наиболее эффективны для оценки знаний 3-факторные тесты, описанные и проиллюстрированные примерами в работах [18, 19]. В связи с этим в настоящей статье подробно рассматривается процесс составления, использования и последующей обработки именно 3-факторных тестов.
На основе методики составления многофакторных двухуровневых тестов были сконструированы тестовые задания и проведено тестирование для выявления знаний обучающихся, изучающих дисциплину «Теория автоматического управления». Каждому испытуемому было предоставлено девять различных трехфакторных ТВ Q i , отражающих знание подраздела «Линейные непрерывные модели и характеристики систем управления». На каждый из этих ТВ по теории двухуровневого трехфакторного эксперимента можно составить комбинаторно различное множество A i из восьми комплексных ответов A ij . В данном примере испытуемым предлагалось множество A i из четырех вариантов комплексных ответов A ij , включающих различные совокупности ответов a itj и a ifj . Такие тесты названы авторами усеченными трехфакторными (УIIIФ-тесты).
Тесты построены на основе сформулированных ФЗ, позволяющих, по мнению разработчиков, по факту понимания их сущности оценить уровень подготовки тестируемых по данной теме. В соответствии с изложенной в [18, 19] методикой каждое усеченное задание сформулировано как тестовый вопрос (ТВ), на который предлагалось четыре варианта ответов, выбранных случайным образом из полного трехфакторного тестового задания, содержащего 8 вариантов ответов.
Содержание этих усеченных трехфакторных ТВ приведены в таблице 1. В этой таблице использованы следующие обозначения: ПФ — передаточная функция; ДЗ — динамическое звено; ДУ — дифференциальное уравнение; ЛАЧХ — логарифмическая амплитудная частотная характеристика; ФЗ — фактор знания; АФЧХ — амплитудная фазовая частотная характеристика; АЧХ — амплитудная частотная характеристика; ФЧХ — фазовая частотная характеристика; ВЧХ и МЧХ — вещественная и мнимая частотные характеристики; ММ — математическая модель; ХП — характеристический полином.
Предложенные рассматриваемыми в таблице 1 вариантами ТВ правильные и неправильные ответы, относящиеся к включенным в него ФЗ, сведены в таблицу 2.
Таблица 1
Примеры усеченных трехфакторных тестовых вопросов
|
№ ТВ (ТВ i ) |
№ ФЗ в ТВ i |
Формулировка фактора знания |
Формулировка тестового вопроса |
|||||
|
ТВ 1 |
х 1 |
связь структуры ПФ со структурой линейного ДУ ДЗ |
По заданному ДУ следующего вида: d 2 y dy dх —Y + 6 — + 5 y = 2— + 12 х , описывающему, ДЗ найти пере- dt 2 dt dt даточную функцию и определить ее нули и полюса. |
|||||
|
х 2 |
смысл понятия нуля ПФ |
|||||||
|
х 3 |
смысл понятия полюса ПФ |
|||||||
|
ТВ 2 |
х 1 |
тип ДЗ |
▲ L(w) 40 s 201g к 0 Z> ► >8"' |
По виду асимптотической ЛАЧХ ДЗ L ( w ) , проходящей через точки 20 дБ и +1, выявить суть ФЗ. |
||||
|
х 2 |
ПФ ДЗ |
|||||||
|
х 3 |
наклон ЛАЧХ ДЗ |
|||||||
|
ТВ 3 |
х 1 |
ПФ в общем виде |
j lL(w) 40 / 20 20 lg^ / *+20 дБ\дек 0 1 |
По виду асимптотической ЛАЧХ ДЗ определить ПФ в общем виде, коэффициент усиления и значение постоянной времени. |
||||
|
х 2 |
значение коэффициента усиления |
|||||||
|
х 3 |
значение постоянной времени |
|||||||
|
ТВ 4 |
х 1 |
представление ПФ ДЗ в частотной форме - АФЧХ |
По передаточной функции ДЗ W(p) = — определить ча- 4 р стотные характеристики: АФЧХ, АЧХ и ФЧХ. |
|||||
|
х 2 |
получение АЧХ по ПФ |
|||||||
|
х 3 |
получение ФЧХ по ПФ |
|||||||
|
ТВ 5 |
х 1 |
получение ВЧХ по ПФ |
По передаточной функции ДЗ W(p) = 50 р , найти частотные характеристики: ВЧХ и МЧХ и представить ПФ в показательной форме. |
|||||
|
х 2 |
получение МЧХ по ПФ |
|||||||
|
х 3 |
Представление ПФ ДЗ в показательной форме |
|||||||
|
ТВ 6 |
х 1 |
получение коэффициента усиления по ПФ |
По ПФ w ( p ) = —120 p + 12— определить коэффициент p 3 + 10 p 2 + 100 p усиления k, оценить условие физической реализуемости и наличие или отсутствие астатизма. |
|||||
|
х 2 |
знание условия реализуемости ПФ |
|||||||
|
х 3 |
оценка астатизма по ПФ |
|||||||
|
ТВ 7 |
х 1 |
нахождение системной матрицы А |
. x 1 = x 1 + x 2 , . X 2 =- 5 X j + X 3 , . x 3 x = - 3 x 1 - 2 x 2 - x 3 + 4 u , У = x i. |
По ДУ в переменных состояния, получить ММ объекта в матричновекторной форме |
||||
|
х 2 |
нахождение матрицы управления В |
|||||||
|
х 3 |
нахождение матрицы выходов С |
|||||||
|
ТВ 8 |
х 1 |
нахождение ПФ в общем виде |
;l Im -X—X--►^ p=O/ p= -0,1 |
По расположению корней ХП ПФ на комплексной плоскости определить ПФ в общем виде, тип корней и значение постоянных времени. |
||||
|
х 2 |
определение типа корней |
|||||||
|
х 3 |
нахождение постоянных времени |
|||||||
Информатика, вычислительная техника и управление
|
№ ТВ (ТВ i ) |
№ ФЗ в ТВ i |
Формулировка фактора знания |
Формулировка тестового вопроса |
||
|
ТВ 9 |
х 1 |
определение по ЛАЧХ ПФ в общем виде |
. lUw) ™^V4O дБ\дек 77----------- ' ► lgw 0 W] W2 |
По виду ЛАЧХ ДЗ определить ПФ в общем виде, наличие астатизма и сопрягающую частоту. |
|
|
х 2 |
определение по ЛАЧХ наличие астатизма |
||||
|
х 3 |
нахождение сопрягающей частоты |
||||
Таблица 2
Правильные и неправильные ответы по факторам ТВ таблицы 1
|
X |
О НН о Е О О Н м |
Ответы по факторам знания |
|||||
|
х 1 |
х 2 |
x 3 |
|||||
|
к |
ТВ 1 |
.... . 2 p + 12 W ( Р ) = 2 \ с p + 6 p + 5 |
Нуль: p = - 6 |
Полюсы: p =- 1; р = - 5 |
|||
|
ТВ 2 |
Интегрирующее звено |
1 0,1 - p |
- 20 дб\дек |
||||
|
ТВ 3 |
W ( p ) = к - (Тр + 1) |
к = 10 |
Т = 0,1 |
||||
|
ТВ 4 |
W ( jw) = - 0,25 jw 1 |
А ( w ) = 0,25 w 1 |
П ф( w ) = - 2 |
||||
|
Ч к |
ТВ 5 |
Re( w ) = 0 |
Im( w ) = 50 jw |
W ( jw ) = 50 w - e1 2 |
|||
|
ТВ 6 |
к = 0,12 |
ПФ — физически реализуемая |
астатическая |
||||
|
ТВ 7 |
А = |
110 - 5 0 3 - 3 - 2 - 1 |
В = |
) ) |
С = 1 0 0 |
||
|
ТВ 8 |
W ( p ) =------- k------- ( T 1 p + 1) - (Т 2 р + 1) |
вещественные полюса |
Т 1 = 2 , Т 2 = 10 |
||||
|
ТВ 9 |
W(p) = 2 2 k------ (T 2 p 2 + 2^ Тр + 1 ) |
объект статический |
w 1 — сопрягающая ча стота |
||||
|
R |
ТВ 1 |
\ p 2 + 6 p + 5 W ( p ) = _, 2 p + 12 |
Нули: p = - 1; р = - 5 |
Полюс: p = - 6 |
|||
|
ТВ 2 |
Дифференцирующее звено |
20 - р |
+20 дб\дек |
||||
|
1) ° в 8 О Н m |
Ответы по факторам знания |
|||||
|
х 1 |
х 2 |
x 3 |
||||
|
ТВ 3 |
W(p) = —к— (Tp + 1 ) |
к = 20 |
Т = 10 |
|||
|
ТВ 4 |
W( jw) = — 0 , 25 jw |
A(w) = - 0 , 25 jw |
Ф ( w ) = +n |
|||
|
ТВ 5 |
Re(w) = 50 |
Im( w) = jw |
W(jw) = - 50 w ■ e1 |
|||
|
ТВ 6 |
к = 0 , 1 |
ПФ — физически не реализуемая |
статическая |
|||
|
ТВ 7 |
А = |
110 - 5 3 0 - 3 - 2 - 1 |
В = |
I |
С = 1 0 0 |
|
|
ТВ 8 |
W(p) = к ■ (T , p + 1) ■ (Т 2 р + 1 ) |
мнимые нули |
Т , = 0,5 Т 1 = 0,1 |
|||
|
ТВ 9 |
W(p) = к ■ (T 2 p 2 + 2^ Тр + 1 ) |
объект астатический |
w 2 — сопрягающая частота |
|||
По вопросам таблицы 1 была проведена аттестация группы студентов. На каждый вопрос предлагалось по четыре варианта ответа, составленных из правильных и неправильных ответов по ФЗ вопроса из таблицы 2. При этом выполнялось условие (5). Общее количество тестируемых составило 10 человек. Оценки ответов и результаты их обработки сведены в таблицу 3.
В таблице 3 цветом выделены вопросы, в которых тестируемые выбрали две строки ответов.
Расчет тестовых оценок начинается с получения оценки ответа j -го тестируемого на i -й тестовый вопрос e ij . Это оценка рассчитывается как среднее значение оценок строк тестового вопроса, которых выбрал тестируемый:
1 k
eij = ■£ elj, k l=1
где к — количество выбранных строк ответов в j -м тестовом задании ( к < 2).
Допущенная вариативность ответа позволяет ввести меру неравномерности знаний испытуемым всех ФЗ i -го
ТВ g ij . Она рассчитывается по формуле:
g i = \ 117■ Ek - e «)2 . k 1 l = 1
Усредненное знание j -м испытуемым всех ФЗ из n вопросов теста естественно оценить показателем е j , рассчитываемым по формуле:
n ej="n £ ' i=1
Информатика, вычислительная техника и управление
Таблица 3
Ответы по факторам ТВ таблицы 1 и данные их обработки
|
№ теста (i) |
Номер тестируемого (j) |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
||||||
|
(’v) / /) ’ 2 ) / |
(eDi/ /°(e^i 1 |
(’v) / X ’ 2 ) / |
(^l/ //a Wi? |
(’v)/ /( ’ 2 ) / |
(S) / y/O (e) i 3 |
(ev) / /)22 )/ |
(el)/ /^ /^(e ) i 4 |
(ev) / /) ’ 2 ) i |
(ei) i Xх /^ 17(e)i5 |
|
|
1 |
0,67 |
0,67 |
0,67 |
0,67 |
1 |
1 |
0 |
0,165 |
0,67 |
0,67 |
|
0,67 |
0 |
0,67 |
0 |
1 |
0 |
0,33 |
0,054 |
0,67 |
0 |
|
|
2 |
0,67 |
0,67 |
1 |
1 |
1 |
1 |
1 |
0,835 |
0,67 |
0,67 |
|
0,67 |
0 |
1 |
0 |
1 |
0 |
0,67 |
0,054 |
0,67 |
0 |
|
|
3 |
0 |
0 |
1 |
1 |
1 |
1 |
0,33 |
0,5 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0,67 |
0,057 |
1 |
0 |
|
|
4 |
0,67 |
0,67 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0,67 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
|
5 |
1 |
0,665 |
0,33 |
0,33 |
1 |
1 |
1 |
1 |
0,33 |
0,33 |
|
0,33 |
0,224 |
0,33 |
0 |
1 |
0 |
1 |
0 |
0,33 |
0 |
|
|
6 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0,835 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0,67 |
0,054 |
|
|
7 |
1 |
0,835 |
0,33 |
0,33 |
0,67 |
0,67 |
1 |
1 |
1 |
0,835 |
|
0,67 |
0,054 |
0,33 |
0 |
0,67 |
0 |
1 |
0 |
0,67 |
0,054 |
|
|
8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
|
9 |
0,33 |
0,33 |
1 |
1 |
1 |
1 |
1 |
1 |
0,67 |
0,67 |
|
0,33 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0,67 |
0 |
|
|
е js |
0,537 |
0,592 |
0,852 |
0,833 |
0,779 |
|||||
|
σ js |
0,176 |
0 |
0 |
0,136 |
0,11 |
|||||
|
№ теста (i) |
6 |
7 |
8 |
9 |
10 |
|||||
|
(’v) / /) ’ 2 )i |
(e"6)i/X ^/O(e)t6 |
(ev\ / /к2)i |
бХ °(e)i7 |
(ev\/ /) ’ 2 ) / |
(S\/ /6 (e) i 8 |
(ev)// /)2г )/ |
(e9)i//// X" ( e ) i 9 |
(ev)/ /) ’ 2 ) i |
(eio)i/^ y/0 (e) i vo |
|
|
1 |
6 |
0 |
0,165 |
0,67 |
0,67 |
1 |
1 |
0,67 |
0,67 |
|
|
0,33 |
0,33 |
0,33 |
0,054 |
0,67 |
0 |
1 |
0 |
0,67 |
0 |
|
|
2 |
0,33 |
0 |
1 |
0,665 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0,33 |
0,224 |
1 |
0 |
1 |
0 |
1 |
0 |
|
|
3 |
1 |
0 |
1 |
0,665 |
0,67 |
0,67 |
1 |
1 |
1 |
1 |
|
0,33 |
0,33 |
0,33 |
0,224 |
0,67 |
0 |
1 |
0 |
1 |
0 |
|
|
4 |
0,33 |
0 |
0 |
0,165 |
1 |
1 |
0 |
0 |
0,67 |
0,67 |
|
0,67 |
0,67 |
0,33 |
0,054 |
1 |
0 |
0 |
0 |
0,67 |
0 |
|
|
5 |
0,67 |
0 |
0,33 |
0,33 |
1 |
1 |
1 |
1 |
0,67 |
0,67 |
|
0,33 |
0,33 |
0,33 |
0 |
1 |
0 |
1 |
0 |
0,67 |
0 |
|
|
6 |
0,67 |
0,67 |
0 |
0 |
1 |
1 |
1 |
1 |
0,67 |
0,67 |
|
0,67 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0,67 |
0 |
|
|
7 |
0,67 |
0,67 |
0,67 |
0,67 |
1 |
1 |
1 |
1 |
0,67 |
0,67 |
|
0,67 |
0 |
0,67 |
0 |
1 |
0 |
1 |
0 |
0,67 |
0 |
|
|
8 |
0,67 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0,33 |
0,33 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
|
9 |
0,33 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0,33 |
0,33 |
|
0,33 |
0,33 |
1 |
0 |
1 |
0 |
1 |
0 |
0,33 |
0 |
|
|
е js |
0,518 |
0,517 |
0,926 |
0,889 |
0,742 |
|||||
|
σ js |
0 |
0,249 |
0 |
0 |
0 |
|||||
Тогда неравномерности знания испытуемым всего материала, охватываемого тестом, оцениваются усредненным значением ст у всех СКО j -го тестируемого, рассчитанных для него по всему тесту (всем ТВ):
n о,=х 1 -Е - j 2. (9)
-
V n М
Таким образом, полученные после статистической обработки факторного теста данные достаточно разносторонни и представительны, т. к. поддержаны всеми ФЗ, входящими во все ТВ теста (в рассматриваемом случае -3х9=27). Наряду с традиционной для процедуры тестирования общей оценкой доли усвоенного материала — ei , а также дифференцированной оценкой хорошо и плохо усвоенных его элементов — eij , факторная структура теста позволяет оценить дополнительные характеристики знания. К таким характеристикам относится возможность более дифференцированной общей оценки каждого ТВ, а также неравномерности знания ФЗ в нем — о у . Также, более дифференцированно оценивается общее знание раздела, т.к. ei характеризуется большей дискретизацией. Кроме того, возникает возможность общей оценки неравномерности этого знания о у .
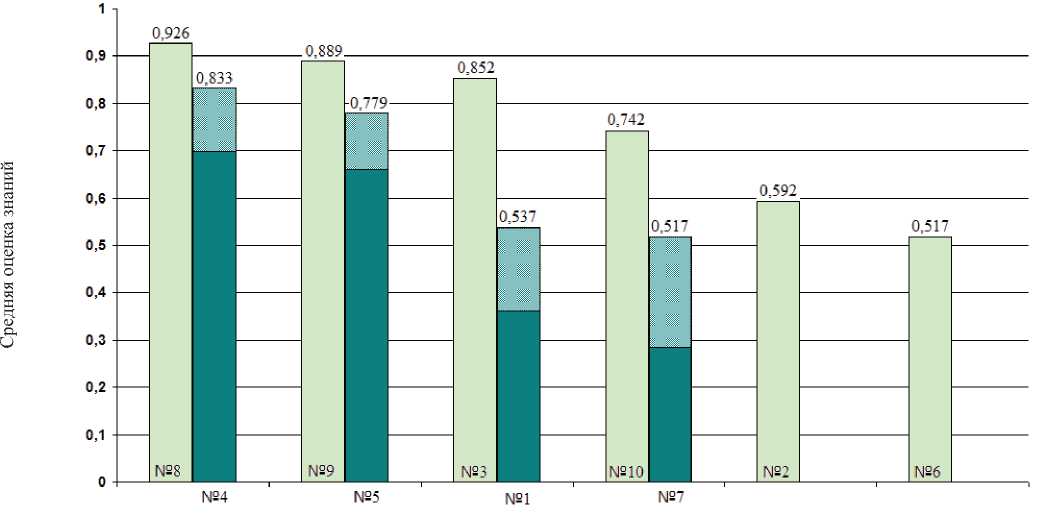
На рис. 1 приведены гистограмма оценки результатов тестирования группы из десяти фигурантов, проходивших тестирование по материалу из таблиц 1, 2, ответы которых приведены в таблице 3. Там же приведены результаты обработки полученных оценок по формулам (6)-(9).
Столбчатые гистограммы построены по полученным усредненным оценкам тестируемых по всему тесту от наилучших результатов к наихудшему.
Столбцы гистограммы № 8, № 9, № 3, № 10, № 2, № 6 построены по оценкам испытуемых, выбравших в качестве ответов по одной строке в каждом тестовом задании. Столбцы гистограммы № 4, № 5, № 1, № 7 характеризуют испытуемых, проявивших неуверенность своих знаний при ответе на определенные тестовые задания и указавших две строки ответов. У этих испытуемых верхушку столбца средней оценки, полученной за тест, «размывает» значение СКО, указывающее на неуверенность знаний тестируемых студентов. Это уменьшает фактическую оценку.
Информатика, вычислительная техника и управление
Тестируемые
Рис. 1. Гистограмма оценки результатов тестирования
Выводы. Рассмотренные примеры тестовых вопросов демонстрируют хороший уровень формализации и удобство составления тестов на основе методики многофакторного планирования двухуровневых экспериментов. Кроме того, хорошо формализуется оценка результатов теста, что повышает его объективность. Важным нововведением является допущение своеобразной «нечеткости» ответа на вопрос теста, и порождаемая этим двухпараметрическая оценка результата теста: оценка неполного знания и степени уверенности этого знания. Результаты тестирований с использованием двухфакторных и трехфакторных тестовых заданий установили роль «факторности» теста, влияющую на ранжирование испытуемых с неуверенными знаниями. Таким образом, предложенная модель оценки результатов факторного тестирования вполне логична, проста и достаточно адекватно отражает состояние знания тестируемого. Она дает дополнительные возможности, как преподавателю для оценки не только среднего знания, но и степени уверенности испытуемого, так и самому тестируемому, давая ему шанс в виде ответов с частичными знаниями. Эти свойства факторного подхода к тестированию подтверждены многократным тестированием студентов кафедры «Автоматизация производственных процессов», изучающих дисциплину «Теория автоматического управления».
Список литературы Исследование эффективности парадигмы факторной оценки знаний на примере тестирования студентов по теории автоматического управления
- Ефремова, Н. Ф. Проблемы формирования фондов оценочных средств ВУЗов/Н. Ф. Ефремова//Высшее образование сегодня. -2011. -№ 3. -С. 17-21.
- Ефремова, Н. Ф. Системность и преемственность в формировании фонда оценочных средств технического ВУЗа/Н. Ф. Ефремова, Б. Ч. Месхи//Совет ректоров. -2011. -№ 5. -С. 33-40.
- Вешнева И. В. Разработка базы моделей интеллектуальной системы мониторинга процесса формирования профессиональных и общекультурных компетенций студентов вузов. Вестник Саратовского гос. техн. ун-та. -2012. -Т.1, № 2(64). -С. 348-355.
- Васин, А. Н. Информационная образовательная среда -путь к повышению эффективности образовательного процесса/А. Н. Васин//Вестник Саратовского гос. техн. ун-та. -2010. -№ 1(44). -С. 121-126.
- Ефремова, Н. Ф. Подходы к оцениванию компетенций студентов первого курса, приступающих к освоению основных образовательных программ/Н. Ф. Ефремова//Вестник Дон. гос. техн. ун-та. -2010. -№ 5. -С. 774-782.
- Ефремова, Н. Ф. Особенности построения региональной системы оценки качества образования/Н. Ф. Ефремова//Вестник Донского гос. техн. ун-та. -2009. -№ 1. -С. 762-772.
- Большаков, А. А. Контроль знаний в интеллектуальной обучающей системе по курсу «Надежность систем автоматизации»/А. А. Большаков, А. Ю. Маркелов//Вестник Саратовского гос. техн. ун-та. -2010. -№ 4(50). -С. 153-156.
- Большаков, А. А. Оценка результативности функционирования автоматизированной обучающей экспертной системы/А. А. Большаков, В. В. Шатохин//Вестник Саратовского гос. техн. ун-та. -2010. -№ 4(50). -С. 149-153.
- Большакова, М. А. Создание автоматизированной обучающей системы для изучения иностранного языка в неязыковых вузах/М. А. Большакова//Вестник Саратовского гос. техн. ун-та. -2010. -№ 4(50). -С. 161-164.
- Большаков, А. А. Управление образовательным процессом на основе автоматизированных комбинированных обучающих систем/А. А. Большаков, О. Н. Долинина, В. В. Шатохин//Вестник Саратовского гос. техн. ун-та. -2008. -№ 3(35). -С. 54-62.
- Черткова, Е. А. Автоматизация анализа и проектирования компьютерных обучающих систем/Е. А. Черткова//Вестник Саратовского гос. техн. ун-та. -2006. -№ 1(11). -С. 97-103.
- Кузнецов, А. В. Оценивание параметров тестов/А. В. Кузнецов//Вестник Саратовского гос. техн. ун-та. -2006. -№ 2(13). -С. 9-13.
- Нейдорф, Р. А. Методология организации тестирования на основе алгоритмов планирования и обработки двухуровневых многофакторных экспериментов/Р. А. Нейдорф, Е. Н. Обухова//Вестник Дон. гос. техн. ун-та. -2014. -Т. 14, № 2 (77). -С. 110-120.
- Нейдорф, Р. А. Методология построения тестов на основе алгоритма планирования двухуровневых многофакторных экспериментов/Р. А. Нейдорф, Е. Н. Обухова//Информационные технологии в управлении (ИТУ-2012): материалы 5-й Рос. мультиконф. по проблемам управления. -Санкт-Петербург, 2012. -С. 861-870.
- Нейдорф, Р. А. Алгоритм расчета и оценки результатов факторно-тестовой оценки/Р. А. Нейдорф, Е. Н. Обухова//Научное обозрение. -2015. -№ 2. -С. 41-56.
- Нейдорф, Р. А. Методика составления тестовых заданий на основе алгоритма планирования двухуровневых многофакторных экспериментов и анализ их использования в образовательном процессе/Р. А. Нейдорф, Е. Н. Обухова//Методики и технологии обеспечения и оценки качества образования сб. материалов междунар. науч. конф. -Киев, 2013. -С. 23-28.
- Обухова, Е. Н. Особенности формирования оценок в строках ответов в двухфакторном тестовом задании/Е. Н. Обухова//Аспирант. -2014. -№ 4. -С. 65-67.
- Нейдорф, Р. А. Анализ применения трехфакторных дробных тестов в учебном процессе/Р. А. Нейдорф, Е. Н. Обухова//Математические методы в технике и технологиях: сб. тр. XXVI междунар. науч. конф. -Н. Новгород, 2013. -С. 320-323.
- Обухова, Е. Н. Построение и исследование тестовых заданий при разбиении их на дробные реплики//Инновация, экология и ресурсосберегающие технологии: тр. X междунар. науч.-техн. форума. -Ростов н/Д, 2012. -С. 363-367.
- Афанасьев, В. В. Теория вероятностей в вопросах и задачах/В. В. Афанасьев. -Ярославль: изд-во Яросл. гос. пед. ун-т им. К. Д. Ушинского, 2004. -249 с.


