Исследование эффективности разведывательно-огневого метода поражения излучающих радиоэлектронных объектов

Анализ локальных войн и вооруженных конфликтов показывает значительное увеличение составляющей высокоточных средств поражения, предназначенных в том числе для уничтожения (вывода из строя) радиоэлектронных объектов противника. Данные обстоятельства, в свою очередь, накладывают жесткие требования к информационной компоненте обеспечения высокоточного поражения как по оперативности, так и по точности вскрытия пространственного размещения уничтожаемых объектов.

Изложенное свидетельствует о высокой интеграции и тесной взаимосвязи информационной и огневой составляющих вооруженного конфликта, что предопределяет возможные взаимные ограничения на количественные значения показателей эффективности каждой из рассматриваемых компонент.

Исходя из этого, целью настоящей статьи является разработка метода, позволяющего с системных позиций реализовать учет возможного влияния разведывательной составляющей информационного обеспечения на процесс огневого поражения радиоэлектронных объектов противника.

Наиболее целесообразно в качестве показателя эффективности огневого поражения излучающего радиоэлектронного средства РЭС определить вероятность поражения P _пор( t ) как величину, отражающую реализацию основного функционала средств поражения и фактически являющуюся оценкой возможности по уничтожению радиоэлектронного объекта РЭОб.

Структурная модель огневого воздействия на РЭОб, сформированная исходя из особенностей внутрисистемных взаимосвязей элементов рассматриваемого процесса, представлена на рис. 1.

Исходя из структуры представленной модели поражения, динамическую модель сформируем в виде ориентированного графа состояний (рис. 2).

На рис. 2 приняты следующие обозначения:

• С 0 – исходное состояние;

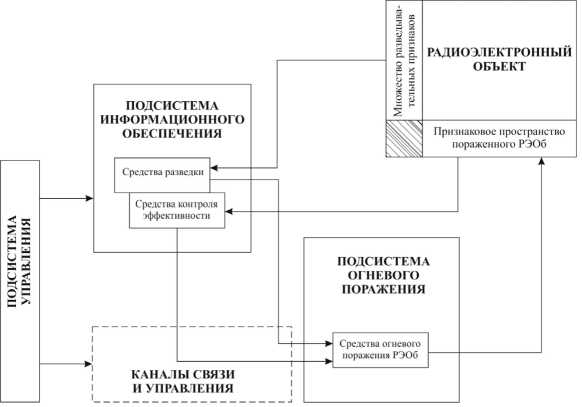
Рис. 1. Структурная модель процесса поражения излучающих РЭС

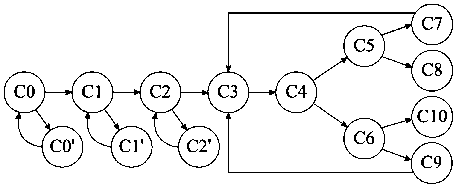
Рис. 2. Ориентированный граф состояний, отражающий динамику комплексного поражения РЭС

• С 1 – поиск и обнаружение РЭС (РЭС обнаружено);

• С₀' – РЭС не обнаружено;

• С 2 - высокоточное определение координат РЭС, подлежащих поражению (оценка координат РЭС произведена);

• С 1 ' – оценка координат РЭС не произведена;

• С 3 - передача информации на огневые средства (артиллерийские батареи) поражения (информация на средства поражения передана);

• С₂' – информация на средства поражения не передана;

• С 4 – попадание снаряда в заданный сектор;

• С₅ – РЭС не поражено;

• С 6 – РЭС поражено;

• С₇ – принятие решения о том, что цель не поражена при ее непоражении;

• С 8 – принятие решения о том, что цель поражена при ее непоражении;

• С₉ – принятие решения о том, что цель не поражена при ее поражении;

• С 10 – принятие решения о том, что цель поражена при ее поражении.

В качестве математической модели процесса поражения рассмотрим полумарковский процесс, протекающий на множестве состояний представленного ориентированного графа.

Введем в рассмотрение передаточную функцию перехода графа ( С , - ^ С) в следующем виде:

h_y ( s ) = L { P j ф у (t)}, (1) где P j ф у (t) - вероятность и плотность вероятности распределения времени ожидания при переходе из i -е в j -е состояние соответственно [1].

В соответствии с передаточной функцией перехода сформируем динамическую модель процесса поражения в виде передаточных функций (рис. 3) [1, 2].

Исходя из топологической структуры модели интервальные вероятности для состояний, характеризующего поражение цели, получим следующее аналитическое соотношение:

P ( s ) =         P 0 H h 0 , 1 ( s ) h l , 2 ( s ) h 2 , 3 ( s ) h 3 , 4 ( s ) h 4 , 6 ( s ) h 6 , 10 ( s )         _x

• ^{10        ( 1} — h 0 , 0' ⁽ s ) h 0' , 0 ⁽ s № — h , 1' ⁽ s ) h 1' , 1 ( ^s № — ^h 2 , 2' ⁽ s ) h 2' , 2 ⁽ s ) )

  
  

____________________1______________________________________

• ¹    — ⁽ h 3 , 4 ⁽ s ) '⁽ h 4 , 5 ⁽ s ) h 5 , 7 ⁽ s ) h 7 , 3 ⁽ s ⁾⁺ h 4 , 6 ⁽ s ) h 6 , 9 ⁽ s ) h 9 , 3 ⁽ s ) )) ’

  

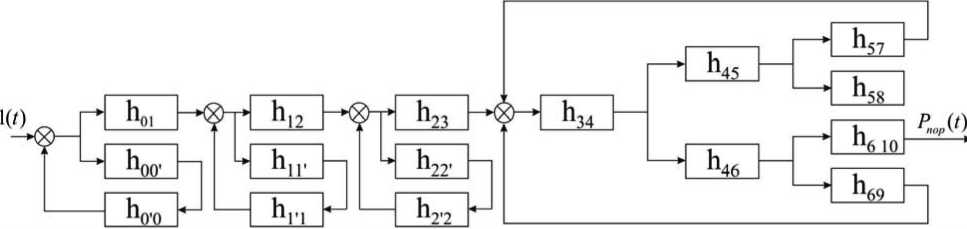
  Рис. 3. Динамическая модель процесса поражения

  
  

Окончательно искомая вероятность при единичном ступенчатом воздействии может быть представлены в виде

( t ) = L -¹ Г 1 P ( 5 ) . £

В интересах обоснования множества исходных данных рассмотрим более детально каждое из состояний приведенного выше графа.

Переход C 0 ^ C 1 связан с вероятностно-временными характеристиками поиска РЭС и выделения истинной цели среди совокупности ложных целей в условиях непреднамеренных и преднамеренных помех.

Поисковую составляющую моделируемого процесса рассмотрим на основании реализации триангуляционно-корреляционного метода местоопределения [3, 4].

Способ заключается в реализации синхронного по пространству и времени пеленгования источников излучения с последующей корреляционной обработкой потока сигналов от каждого из пеленгаторов. Пространственно-временная синхронизация реализуется путем одновременного формирования диаграмм направленности пеленгаторов, направления максимумов которых ориентированы на геометрический центр просматриваемого элемента области поиска.

Для решения задачи поиска истинной цели допустим, что в секторе поиска находится одно РЭС, P D (t ) - вероятность правильного обнаружения, T a - время анализа элемента разрешения, M = M x хM y - число элементов поиска, P ( x, у ) или P ik - вероятность попадания в элемент разрешения.

Опираясь на результаты, полученные в [2], безусловную вероятность правильного обнаружения сигнала определим в следующем виде:

M

P d = Е D k ■ P ' П Fj’ (! - P¹')-

к=1

Для случая равновероятного распределения с перераспределением вероятностей от эле-

D к мента к элементу сектора поиска P, =        , принимая во внимание неизменность услов- m - к +1

ных вероятностей D и F в каждом из элементов разрешения, получим:

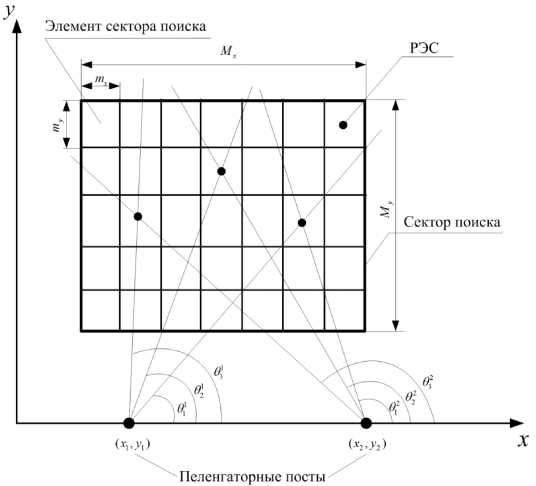
Рис. 4. Триангуляционно-корреляционный метод местоопределения

M

P d = ^- Z F k ^{- 1} .

m k = 1

С учетом времени, затрачиваемого на принятие решения при анализе, окончательное выражение для вероятности правильного обнаружения запишем в виде

M

P d ( t ) = ^- Z ^F k ^{- 1} • h ( t — ^kT a ), m k = 1

где h ( t ) - функция Хэвисайда.

Для перехода C 0 → C 1 приближенно можно воспользоваться финальной вероятностью и средним временем обнаружения, при этом положив:

Ф 01 ⁽ t W⁽ t-T o6H ),

Р 01 ^{= P} 0 - ⁼ lim P D ⁽ t ^).

t

Путем несложных математических преобразований с учетом результатов, изложенных в [2], исходя из (6), ^для T_o6H ^и P 0 D находим:

т =т обн a

1-( M -1) F^{1 M} +MF^{M +1}

(1- F¹ Х1- F ^ M )

P 01= P o D=- m

F^{1 M} -1 "7^?

•

Выражения (8) и (9) описывают процесс поиска и учитывают все составляющие этого про -цесса.

Рассмотрим переход C 1 ^ C 2 , который непосредственно связан с оценкой координат источника радиоизлучения. Время, затрачиваемое на оценку координат, представляет собой детерминированную величину в силу неизменности условия просмотра сектора поиска от цикла к циклу. Однако в этом случае возникает методическая сложность в определении вероятности перехода. Если в основу физической трактовки перехода положить событие, состоящее в том, что оценка местоположения излучающих РЭС будет осуществлена с точностью не хуже заданной по координатам х и у , то вероятность этого события можно использовать в качестве переходной вероятности C 1 ^ C 2 .

Определим указанную вероятность. С этой целью воспользуемся распределением ошибки определения местоположения излучающих РЭС по соответствующим координатам. При этом будем полагать, что оценка ошибки несмещенная, среднее значение ошибки приравниваем к нулю ( m x = m y = 0), а истинное положение излучающего РЭС совпадает со средним значением ошибки. Кроме того, предположим, что воздействие помех сказывается лишь на дисперсии распределения ошибок по координатам х и у.

В этом случае произведение переходной вероятности на плотность распределения времени перехода из состояния C1 в состояние C2 определяется выражением h12 (5) = РпЧ>12 (5) =

f h Л 1 - 2 F\hx- I

VИ x Z

f h

1 - 2 F -y-

И

V y.

■) ■ exp (-ST) ,

где T ₀ - время, затрачиваемое на оценку координат излучающего РЭС после его обнаружения; ст x ² , ст 2 - дисперсии ошибок местоопределения, которые рассчитываются исходя из особенностей триангуляционно-корреляционного метода координатометрии источника радиоизлучения [5, 6]; F ( x ) - функция Лапласа плотности распределения ошибки местоопределения.

Таким образом, полученные выражения характеризуют с вероятностной точки зрения переход C 1 ^ C 2 и учитывают точностные и динамические возможности при оценке местоположения излучающего РЭС.

Переход C₂ ^ C 3 связан с подготовкой и передачей информации на средства огневого поражения. Время передачи информации будет зависеть от используемых для этой цели средств, а также от сложившейся помеховой обстановки.

Передача сообщений реализуется с помощью помехоустойчивого кодирования.

Усредненная вероятность битовой ошибки вычисляется по формуле

n

P b = - Е ( i + 1 ) C n Р(1 — P ) n ^- i, n = t + 1

i n !

где C_n =        ; n - общее число бит информации; t - число исправляемых битовых ошибок;

i !( n - i )!

p – вероятность ошибочного приема канального символа, которая определяется типом сигнала.

К примеру, для сигнала BFSK

P = ^- ■ exp ^f- q | ,                                                       (12)

„ Ec k где q =---- отношение сигнал-шум; k - количество информационных символов сообще-

Nо n ния.

Произведение переходной вероятности на плотность распределения времени перехода из состояния С₂ в состояние С₃ определяется выражением

P ^C t ) = (1 - P_B ) ^L 8 ( t - T_x),                                               (13)

где T — среднее время передачи сообщения; L - число элементов сообщения.

Переход С₃ ^ С₄ характеризуется временем полета снаряда и величиной отклонения снаряда от расчетной точки в плоскости цели. Будем полагать, что в силу случайностей, связанных с удалением РЭОб от средства поражения, время полета снаряда зададим экспоненциальным законом распределения, т.е.

Ф з4 ⁽ t ) = у exp I^- Y | ,                                                     ⁽¹⁴⁾

_                          ^T 2 V ^T 2 )

где Т ₂ - время полета снаряда, полученное на основе усреднения по всем ситуациям, складывающихся значений при поражении РЭОб.

Вре^мя ожидания при переходе C 4 ^ ^С 5 ^{и С} 4 ^ ^С 6 равно 0.

Вероятности переходов С 7 ^ С₃ и С₉ ^ С₃ равны 1.

Переходы С₅ ^ С 7 , С₅ ^ С₈ , С₆ ^ С₉, С₆ ^ С 10 по сути представляют из себя процесс доразведки.

С учетом полученных переходных вероятностей и плотностей распределения времени переходов конечное выражение для вероятности поражения объекта принимает вид

P_w( t ) = L - ¹ ^

1 s

0 i    0 D

• exp ( - s [ T_i4i + T + T ] ) 1 - 2 F I h ^ |

^{L J7} L       V ° - ).

( 1 ^- ( 1 ^{- P} 0 D ) • exP ( ^{- sT}_i4i) ) ¹

-

I

1 -

V V

1 - 2 F I h ^- V ° -

1 - 2 F I h y

V ° y.

f h_v 1 - 2 F

V ° y

p ; _i6 • (i - P b ) ^L • i/f s +11 d

T ²/^V Ti f

( 1 - ( 1 - (1 - P b ) ^L )• e- ^sTT ) -I 1 - _¥ \ s + _¥ |- ( ( 1 - F_[id ) - ( 1 - p;_i6 ) + p;_i6

V ^T 2/ V ^T 2 )

)

• ^exP ( ^{- sT} o )

)

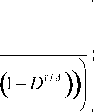
На графиках представлены зависимости вероятности поражения, полученные для следующих исходных данных: D = 0,9; F = 10 ^-4 ; T_a = 40 мкс; о _-у = 20 м; h_-y = 40 м - требуемые размеры области неопределенности для подсистемы поражения; для выбранного кода Голея n = 24, к = 12, t = 3; q = 5; T = 1 мс; P"_op = 0,8 - полигонная вероятность поражения; D^nop = 0,9 - условная вероятность правильного решения при поражении; F^nop = 10 ^-3 - условная вероятность ложной тревоги.

Анализ зависимостей, представленных на рис. 5, позволяет сделать следующие выводы.

Вероятностно-временные показатели уничтожения излучающего объекта существенным образом зависят от динамических и вероятностных характеристик средств огневого поражения. Так, уменьшение полигонных значений вероятности поражения с 0,8 до 0,6 приводит к увеличению времени, необходимого для достижения заданного уровня конечных показателей более чем в 2 раза.

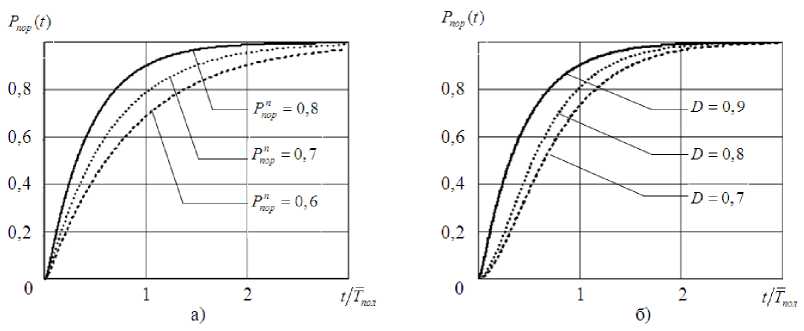
Рис. 5. Графики зависимостей вероятности поражения от относительного времени при различных вероятностных значениях подсистем: а – подсистемы огневого поражения; б – подсистемы обнаружения

Динамические характеристики процессов поиска и координатометрии, а также их «точечные» вероятностные показатели (условные вероятности правильного обнаружения и ложной тревоги, функция распределения оценочных значений координат излучаемого РЭС) в случае сопоставимого значения среднего времени их реализации с динамическими параметрами полета средства поражения в значительной мере влияют на величину конечного показателя либо на временные параметры поражения. Так, при уменьшении условной вероятности правильного обнаружения с 0,9 до 0,7 вероятность поражения цели уменьшается на 17 % (при неизменном времени вероятностных отсчетов).

Таким образом, рассмотренный подход позволяет с единых методических позиций за счет использования математического аппарата полумарковских случайных процессов рассмотреть и взаимно увязать по вероятностным показателям процессы поиска, координатометрии, передачи информации на средства огневого поражения и уничтожения излучающего РЭОб. Результаты исследования возможно использовать как для оценки эффективности каждой составляющей моделируемого процесса, так и для формирования требований к соответствующим подсистемам по значениям показателя уничтожения РЭОб.