Исследование эффективности системы активной виброзащиты с различными типами регуляторов
Автор: Абакумов Александр Михайлович, Рандин Дмитрий Геннадьевич, Азаров Дмитрий Николаевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 6-3 т.17, 2015 года.
Бесплатный доступ
В статье проведено сравнение эффективности системы активной виброзащиты при использовании различных типов регуляторов. На основании полученных ранее в других работах авторов аналитических зависимостей в виде передаточных функций звеньев системы автоматического управления виброзащитой синтезирован регулятор, обеспечивающий желаемый вид логарифмической амплитудно-частотной характеристики замкнутой системы. Эффективность замкнутой системы виброзащиты при действии возмущающего воздействия случайного характера оценивается по принятому квадратичному критерию качества. Проведено сравнение полученных расчетных значений принятого критерия качества при использовании оптимального и регулятор, обеспечивающий желаемый вид логарифмической амплитудно-частотной характеристики замкнутой системы.
Система активной виброзащиты, частотные характеристики, оптимальный регулятор, критерий качества, управляемый магнитореологический демпфер
Короткий адрес: https://sciup.org/148204330
IDR: 148204330 | УДК: 681.516.7
Research of the effectiveness of the active vibration isolation system with different types of regulators
In article comparison of effectiveness of active vibration isolation system with various types of regulators is carried out. On the basis of received earlier in other articles of authors of analytical dependences in the form of transfer functions of links of system of automatic control of vibroprotection the regulator providing a desirable type of the logarithmic amplitude-frequency characteristic of the closed system is synthesized. On the basis of received earlier in other authors articles of analytical dependences in the form of transfer functions of object of vibration isolation system the regulator providing a desirable type of the logarithmic amplitude-frequency characteristic of the closed loop system is synthesized. Efficiency of the closed loop vibration isolation system at action of the random disturbance with variable parameters is estimated by the accepted square criterion of quality. Comparison of the received calculated data of the adopted criterion of quality with using optimal and the regulator providing a desirable form of the logarithmic amplitude-frequency characteristic of the closed loop system is carried out.
Текст научной статьи Исследование эффективности системы активной виброзащиты с различными типами регуляторов
где U - напряжение на обмотке электромагнита демпфера;
к А - коэффициент передачи демпфера; T A 1 , T A 2 - постоянные времени.
С учетом ПФ (1),(2),(3),(4) синтезирован регулятор САВ с МД с использованием логарифмических амплитудно-частотных характеристик (ЛАХ).
На рис. 2 представлены желаемая логарифмическая амплитудная частотная характеристика (ЛАХ) L ^M ( to ) замкнутой САВ с МД.
Вид желаемой ЛАХ Г ЖАЕМ ( to ) сформирован с учетом необходимости снижения до некоторого требуемого значения A 0 или в логарифмическом масштабе до L 0 = 20 lg A 0 виброускорений за-
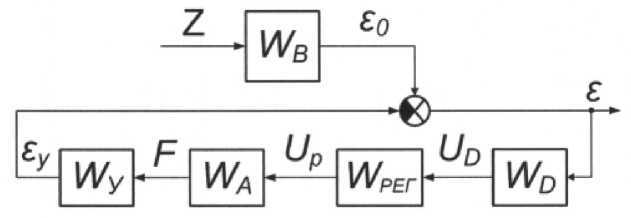
Рис. 1. Структурная схема САВ с МД:
Z - перемещение основания; б - ускорение защищаемого объекта
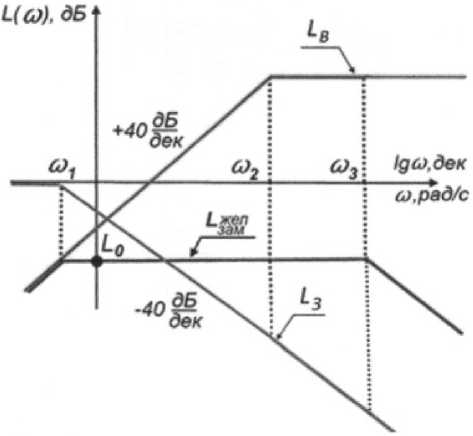
Рис. 2. Частотные характеристики
где A(p), B(p) - полиномы знаменателя и числи-
теля соответственно.
Тогда ПФ замкнутого контура
W 3 (Р) =
£ ( Р ) е о ( Р )
•
1 + W PA3 ( Р )
С учетом (7) ПФ регулятора САВ с МД, обеспечивающего требуемую ЛАХ L3 (ю) замкнутого контура, получена в виде х UP ( р ) 1 - W3 ( р )
WpFF ( Р ) = P ---- =-------------- 3 -------------• (8)
U d ( Р) W y ( Р )W a ( Р )W d ( Р)W 3 ( Р) ( )
По указанной методике получена ПФ регулятора для САВ с МД и численными значениями
параметров: т/С=0,01, ю 1 =0.1 рад/с, ю 2 =10 рад/с,
в 0 =2800
w / (р ) = Up ( p ) W РЕГ ( Р ) тг / X U D ( Р )
0,373 p 4 + 21,4 p 3 + 174,6 p2 + 1919,6 p + 560,7 p
В работе [6] синтезирован оптимальным ре-
щищаемого объекта в частотном диапазоне от ю ^ до ® 2 (или в логарифмическом масштабе от 20lg ю х до 20lg ю 2 ) [5].
Низкочастотный ( ю < ю 1 ) участок желаемой ЛАХ L ^M ( ю ) принят совпадающим с Lb ( ю ) -это упрощает структуру регулятора. ЛАХ Lb ( ю ) получена из ПФ (1) путем приравнивания к нулю постоянной времени T 2 в числителе, определяющей свойства защищаемого объекта на зарезонансных частотах.
гулятор САВ с МД
W^t ( Р ) =
U p ( Р )
3 , 2 , a 0 p + ax p + a 2 p + a 3 +
U D ( Р ) (1 + a 6 Р )
a 4 a 5/
+
/Р /рР
ЛАХ замкнутого контура L 3 ( ю ) определяется по выражению
L 3 ( ю ) = L™ ( ю ) - Lb ( ю ) .
Передаточная функция замкнутого контура с учетом вида L 3 ( ю ) на рис.2 должна иметь вид
(10) где а0 =5,3 . 10-10; а1 = 4,2 . 10-6; a2 =8,9 . 10-6; а3 =3,4 . 10-4; a4 =2,6 . 10-3; a5 =5,4 . 10-3; а6 =0,19, для случайного возмущающего воздействия со спектральной плотностью мощности (СПМ)
Список литературы Исследование эффективности системы активной виброзащиты с различными типами регуляторов
- Maryam Bitaraf, Osman E. Ozbulut, Stefan Hurlebaus, Luciana Barroso. Application of semi-active control strategies for seismic protection of buildings with MR dampers//Engineering Structures № 32, 2010. Pp. 3040-3047.
- Wang Wei, Xia Pinqi. Adaptive Control of Helicopter Ground Resonance with Magnetorheological Damper//Chinese Journal of Aeronautics № 20, 2007. Pp. 501-510.
- Cristiano Spelta, Fabio Previdi, Sergio M. Savaresi, Giuseppe Fraternale, Nicola Gaudiano. Control of magnetorheological dampers for vibration reduction in a washing machine//Mechatronics № 19, 2009. Pp.410-421.
- Рандин Д.Г. Исследование активной системы виброзащиты с управляемым демпфером//Научно-технический вестник Поволжья. 2012. №4. С.177-175.
- Исследование динамических воздействий на блоки сложных изделий при морской транспортировке/А.М. Абакумов, Г.Н. Мятов, С.В. Широков, Д.Г. Рандин//Вестник МГТУ Станкин. 2012. № 4 (23). С. 56-59.
- Исследование системы активной виброзащиты с управляемым магнитореологическим демпфером при случайном характере возмущения/А.М. Абакумов, Э.Г. Чеботков, Д.Г. Рандин//Вестник Самарского государственного технического университета. Серия «Технические науки». 2014. №4(44).
- Abakumov A.M., Miatov G.N. Control algorithms for active vibration isolation systems subject to random disturbance//Journal of Sound and Vibration. №289, 2006. Pp.889-907.
- Абдулаев Н.Д., Петров Ю.П. Теория и методы проектирования оптимальных регуляторов. Л.: Энергоатомиздат. Ленингр. отд-е, 1985. 240 с.
