Исследование экономических временных рядов с общими трендами на основе методов анализа эмпирических данных

Провайдером финансовых данных является сервис Yahoo! Finance предоставляющий в свободном доступе множество исторических котировок для различных финансовых активов [1]. Для проведения анализа получим набор данных, состоящий из дневных котировок для 346 криптовалют в интервале года.

Для повышения качества данных и улучшения финансовых моделей могут использоваться различные способы восстановления пропущенных значений. Одним из них является метод использования регрессионных моделей. Он позволяет до- статочно точно восстановить пропущенные значения, учитывая закономерности в имеющихся наборах данных [2]. Второй метод представляет собой заполнение неизвестных значений предыдущими записями. Он является менее трудзатратным и позволяет не генерировать фиктивные значения, которые могут существенно отличаться от реальных [3].

Попарным сочетанием получим 59685 наборов данных. На примере полученных данных рассчитаем коэффициент линейной корреляции построив затем функцию распределения и функцию плотности распределения значений (рис. 1).

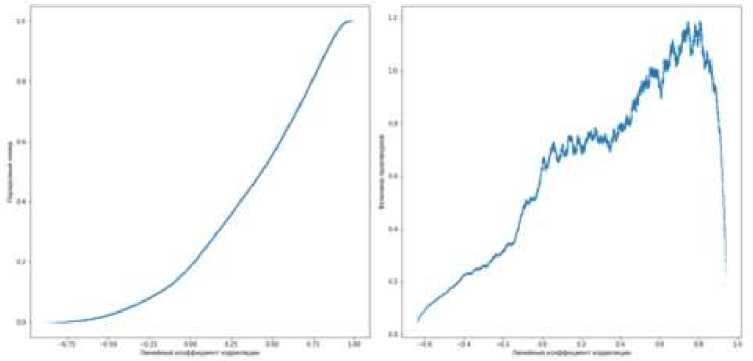
Рис. 1. Распределение значений коэффициентов линейной корреляции

Как можно заметить, исследуемые данные содержат большое количество пар временных рядов со значительной положительной корреляцией, из чего можно сделать вывод о существовании статисти- ческой взаимосвязи между изменениями цен на криптовалюты.

Анализ данных

Рассмотрим пару активов AUTO-USD и

NKN-USD (рис. 2).

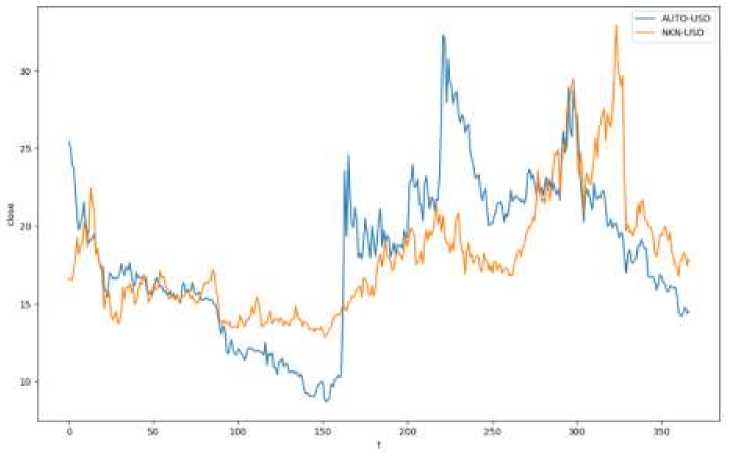
Рис. 2. Пара временных рядов AUTO-USD и NKN-USD

Рассмотрим диаграмму рассеяния дневных цен закрытия торгов для исследуемой пары и рассчитаем коэффициент линейной корреляции г = 0.65 (рис. 3).

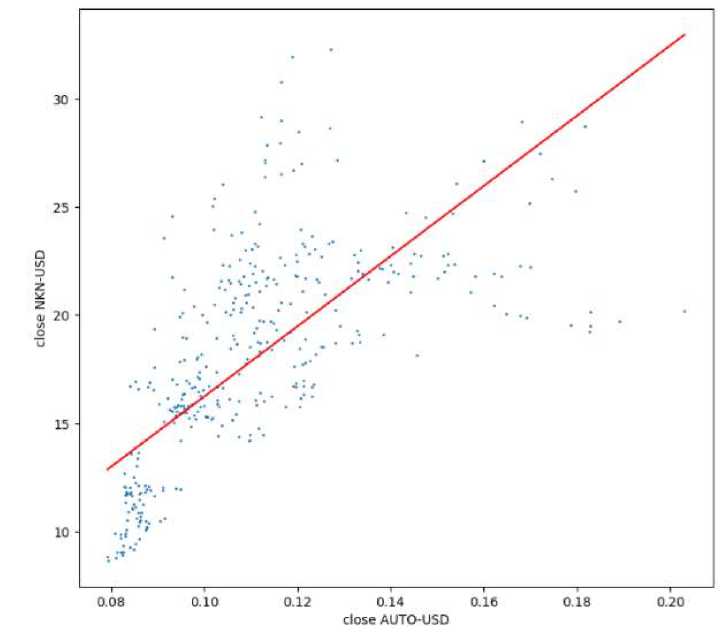
Рис. 3. Диаграмма рассеяния для AUTO-USD и NKN-USD

Методом деления получим спред для каждого торгового дня [4]. Из значения медианы спреда определим коэффициент наклона прямой к. Как итог получим следующую модель взаимосвязи:

ln(162.32xt) ln(1 + 162^-) ~ "(0'-2).

Рассчитаем среднеквадратичное отклонение а = 0.2 и проведем анализ полученного спреда (рис. 4).

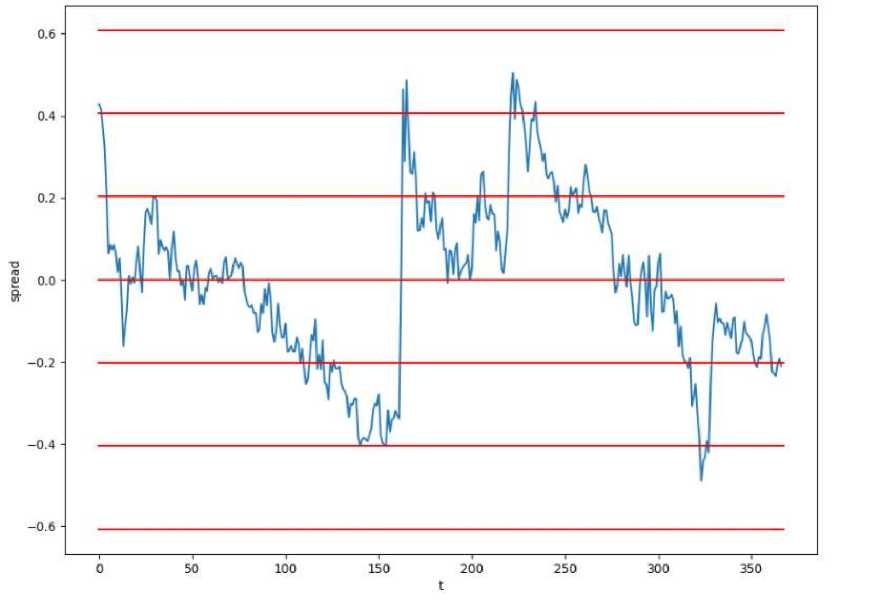
Рис. 4. Спред для AUTO-USD и NKN-USD

Исследуем полученный спред на стационарность, характеризующую неизменность его статистических свойств (табл. 1).

Таблица 1. Анализ стационарности спреда между временными рядами

Вид исследования	Результат
Критерий Манна-Уитни	-1.96 < z < 1.96
Критерий Сиджела-Тьюки	-1.96 < z < 1.96
Критерий KPSS	p > 0.05
Тест Дики-Фуллера	p < 0.05
Критерий Смирнова	p > 0.05

Для выявления почти-периодичности во временном ряде спреда рассчитаем сдвиговую функцию [5] (рис. 5). В результате анализа сдвиговой функции был выявлен почти-период в 240 дней.

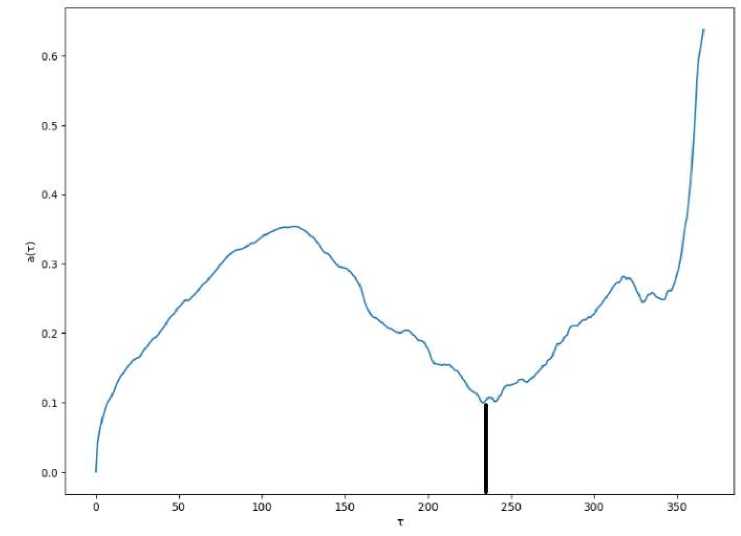
Рис. 5. Сдвиговая функция для спреда AUTO-USD и NKN-USD

Методом оценки плотности ядра построим функцию плотности исследуемого спреда (рис. 6).

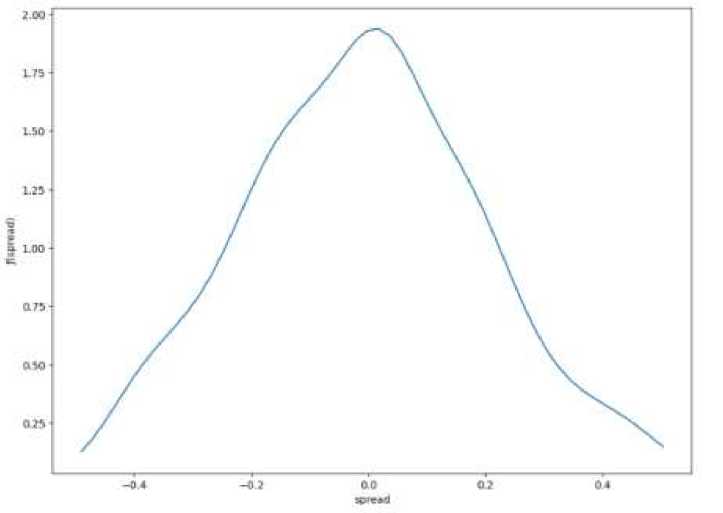
Рис. 6. Функция плотности для спреда AUTO-USD и NKN-USD

Проанализировав функцию плотности, можно сделать вывод о ее соответствии нормальному распределению. Методом анаморфозы для нормального распределе ния определим ее параметры (рис. 7).

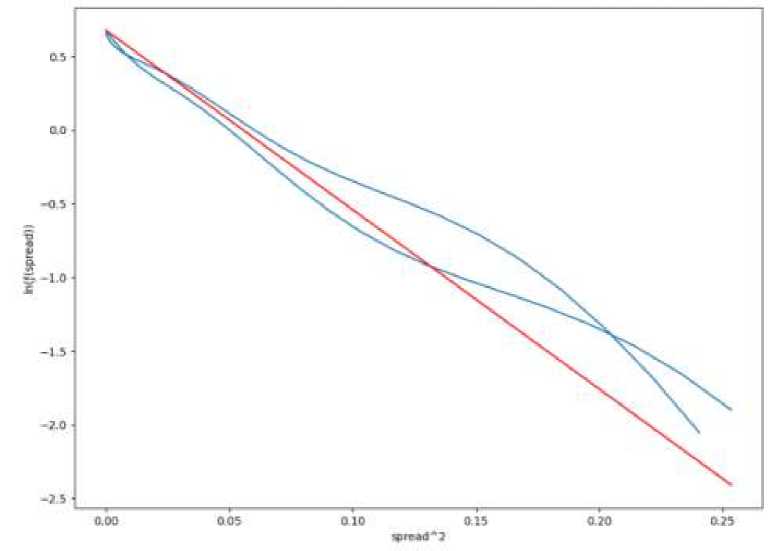
Рис. 7. Анаморфоза функции плотности для спреда AUTO-USD и NKN-USD

Значение стандартного отклонения о = 0.2 полученное с помощью метода анаморфоз совпадает с рассчитанным на этапе получения спреда.

Разделим спред на обучающую и тестовую выборки, где в качестве теста будем использовать последние 40 значений временного ряда. С использованием итерационного метода подберем оптимальные коэффициенты для прогнозирования условной дисперсии (рис. 8):

^t =

^0.004 + 0.9067^1^

™ t

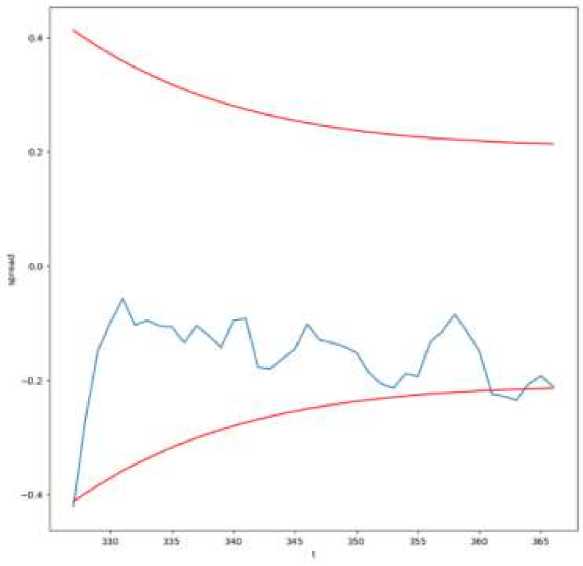
Рис. 8. Прогноз условной дисперсии для спреда AUTO-USD и NKN-USD

Заключение

В результате исследования было получено линейное соотношение для пары финансовых временных рядов. В следствии анализа стационарности остатков был сделан вывод о наличии между ними долгосрочной статистической взаимосвязи. С использованием сдвиговой функции была выявлена почти-периодическая составляющая. С помощью частной автокорреляционной функции был определен порядок авторегрессионной модели. Итерационным методом были найдены оптимальные значения коэффициентов ARCH модели и спрогнозирована условная дисперсия.