Исследование электропривода с многофазным линейным асинхронным двигателем поперечного потока

Рассмотрим некоторые вопросы устойчивости частотно-регулируемого электропривода с линейным асинхронным двигателем (ЛАД) с поперечным потоком (ПП) и статическим преобразователем частоты на основе автономного инвертора тока, в частности осуществление синтеза системы управления на основе аналитических и сравнительно простых частотных методов для линейных непрерывных систем.

Исследование устойчивости привода с ЛАД возможно только на основе комплексного рассмотрения всей системы управления. При этом возникают следующие, в какой-то мере самостоятельные задачи:

• –    разработка практического метода исследования переходных процессов в схемах с автономными многофазными инверторами, при котором связывались бы в единую систему дифференциальные уравнения как звена постоянного тока, так и нагрузки на выходе инвертора. При этом система рассматривается как непрерывная, хотя она и содержит вентильные дискретные преобразователи – инвертор и выпрямитель;

• –    линеаризация нелинейных уравнений линейного асинхронного двигателя;

• –    исследование устойчивости и синтез структуры необходимых регуляторов.

При частотном управлении скольжение двигателя и потребляемый ток устанавливают в соответствии с тяговым усилием, развиваемым двигателем. Но тяговое усилие двигателя не формируется специальным регулятором.

Рассматриваемый тип привода имеет следующие недостатки:

• –    низкое качество регулирования скорости как при управляющем воздействии (изменение частоты), так и при возмущающем воздействии (изменение нагрузочного усилия);

• –    отсутствие режима работы «на упор», из-за чего при чрезмерных нагрузочных моментах привод отключается под действием токовой защиты;

• –    в рамках частотного регулирования трудно реализовать варианты специального управления, когда величина потокосцепления меняется в функции тягового усилия двигателя. При этом напряжение должно регулироваться в функции частоты и тягового усилия.

Решение последней задачи можно упростить, если осуществлять управление амплитудой тока статора, а не напряжения [1]. Амплитуда тока статора определяется моментом (скольжением) двигателя и не зависит от час- тоты. Чтобы непосредственно воспроизводить заданную амплитуду тока, преобразователь частоты должен обладать свойствами источника переменного тока. Такое управление, получившее название частотно-токового, в наиболее типичной форме характеризуется следующими особенностями:

• –    преобразователь частоты является источником переменного тока;

• –    амплитуда переменного тока регулируется в функции частоты скольжения (тягового усилия).

Уравнения автономного инвертора тока. Ток нагрузки однозначно определяется током инвертора id и программой работы коммутатора (рис. 1). Фазные токи запишем в виде i1 = idF1(t),' i 2 = idF2( t),

im   idFm (t), где F1(t),F2(t),...,Fm(t) – функции времени (коммутационные функции), задаваемые программой работы ключей преобразователя и представляющие последовательность разнополярных единичных импульсов, соответствующих включенному состоянию ключей.

Формулы (1) выражают основное отличительное свойство автономных инверторов тока (АИТ). При фиксированной частоте, принимая за начало отсчета момент t = 0, можно записать:

• ₄    sin( n ^π )

• F 1 ( t ) = —V-----—cos n to t ,

πn sin(n π )

42π

F 2 ( t ) = — V-----— cos( n to t --),

π nm

^Fm ⁽ ' ⁾ = П ^

_v ^sin( n ⁿ)   , , 2( m - 1)n.

X> -----3—cos(ntot —^), n             m где ω – частота тока, формируемого инв ертором; n = 2mk ± 1, k = 0,1,2,3, _ .

Учитывая, что в любой момент времени i 1 + i 2 + ... + i_m = 0, получим выражение для результирующего вектора тока нагрузки [2]:

i = —id ^[ F 1^{( 1} ) ^{+ a} F 2⁽¹ ) ⁺ m

+ ... + a      ^F _m ^{( 1 )]} = i d F T ⁽ t ),

где F_T ( t ) – результирующий вектор коммутационной функции инвертора тока.

Так как изменение коммутационных функций фаз

происходит тольк о в моменты коммутации, то результирующий вектор F_T ( t ) в межкоммутационный период имеет постоянную величину и направление, и в моменты, соответствующие моментам коммутации тока в фа-

зах нагрузки, скачком перемещается в положение, состав-

2π

o

ляющее угол m

к прежнему положению. Это переме-

щение соответствует перемещению вектора постоянной

амплитуды, которое происходит не непрерывно, а скачками. Воспользовавшись разложениями функций F ₁( t ), F ₂( t ),..., F_m ( t ) в ряд Фурье, запишем выражение

для результирующего вектора:

F T ( t ) = 2^[ ei ^{ю 1} + π

ГО

+s k=1

¹     ej (2 mk + 1)ш t

2 mk + 1

ГО

-s k=1

¹     e- j (2 mk - 1)m 1 ]

2 mk - 1

F_T ( t ) и F_{T 1}( t ) совпадают друг с другом и с осью фазы, не участвующей в коммутации.

Результирующий вектор коммутационной функции АИТ представляет собой вектор постоянной амплитуды, перемещающейся на фазовой плоскости скачками таким образом, что средняя скорость вращения равна ω [3]. При увеличении числа фаз величина скачков уменьшается, а средняя скорость вращения остается неизменной. При m ^ го величина скачка стремится к нулю и перемещение результирующего вектора коммутационной функции превращается в равномерное вращение со скоростью ω:

F T ( t ) = ^^ e^j » ¹ .                (6)

π

В системе коор д инат, вращающейся со скоростью ω, направив вектор F_T ( t ) вдоль действительной оси, получим

F T ( 1 ) = ²³³ = F_T .                ⁽⁷⁾

π

Уравнения динамики системы с идеализированным автономным инвертором. Для определения зависимости между ^u d ₂ и i_d в переходных режимах при известном дифференциальном уравнении нагрузки необходимо определить зависимости между ^ud ₂ и u . Для этого воспользуемся уравнением баланса мощности, вычисляя мощность нагрузки по выражению

где k = 1, 2, 3, … .

Итак, вектор F_T ( t ) m -фазного мостового инвертора тока представляет собой сумму прямо и обратно вращающихся векторов с различными угловыми скоростями, причем векторы, скорость которых равна (2 mk + 1)ю, вращаются в положительном направлении, т. е. в том же направлении, что и основная гармоника, а векторы, скорость которых равна (2 mk - 1)ю, вращаются в отрицательном направлении.

Основная гармоника

F t 1 ( 1 ) = 2/³ e^j “ ¹                  (5)

π вращается в положительном направлении со скоростью ω. В моменты коммутации тока в двух фазах инвертора, т. е. при ωt, равном 0, π/m, 2π/m и т. д., функции

P e = yRe[ iu ]•                  ⁽⁸⁾

Учитывая (3), получим выражение для реакции автономного инвертора тока:

m ud 2 = yRe[ FT(1) u ]•               (9)

Необходимо отметить, что выражение (9) справедливо для любой системы координат, поскольку мощность m -фазной цепи определяется взаимным расположением векторов тока и напряжения и не зависит от скорости вращения системы координат, в которой они записаны.

При вычислении (9) воспользуемся системой координат, вращающейся в положительном направлении со скоростью ω, при этом де йствительная ось совпадает с направлением вектора F_T ( t ). В этом случае получим АИТ

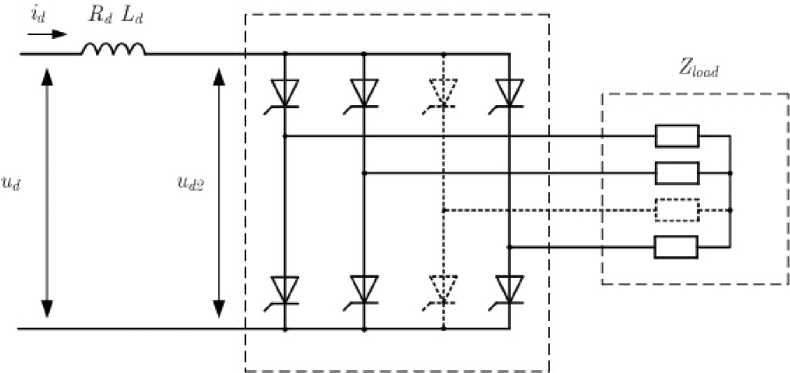
Рис. 1. Схема m -фазного инвертора тока

выражение для реакции АИ как элемента звена постоянного тока:

U d 2 = 2 F t Re[ u ]. (10)

Таким образом, система уравнений, устанавливающая взаимосвязь между входными и выходными величинами АИ с числом фаз m, имеет вид iload = FT id, ud 2 = J FT Re[ uload].

Для исследования динамики системы «АИТ–нагруз-ка» уравнения (11) необходимо решать совместно с уравнением нагрузки, устанавлива ющ им в заи мосвязь между результирующими векторами i _load и u _load нагрузки [3].

Рассмотрим случай, когда процессы в нагрузке описываются линейной системой дифференциальных уравнений и инвертор работает при фиксированной частоте (to = const). В этом случае остается линейной и полная система уравнений, описывающая переходные процессы в системе «АИТ–нагрузка». Записывая уравнения в операторной форме (при нулевых начальных условиях), получим iload(p) = FTid (p), uload ( p ) = Z ( p + j ®) iload ( p ), ud2(p) = J FT Re[uload(p)].

Исследование устойчивости и синтез структуры необходимых регуляторов. Тяговое усилие определяется в равной степени и потоком, и током. Однако в подавляющем большинстве случаев регулируемых приводов при любом типе двигателя управление моментом осуществляется током. Поток как более инерционная величина, ограниченная сверху условиями насыщения магнитной системы, в процессе работы поддерживается неизмен- ным или изменяется по сравнению с током в значительно более узких пределах, причем не для регулирования момента, а для улучшения использования силового оборудования привода (двигателя и преобразователя).

Общий подход к построению управляющих систем для частотно-управляемого асинхронного электропривода вода постоянного тока, и заключается в следующем: по уравнениям электромагнитных процессов в двигателе и электромеханических процессов в приводе составляются структурные схемы, которые дополняются структурными схемами регуляторов, обеспечивающих последовательную отработку основных координат движения системы по принципу отрицательной обратной связи. При реализации систем управления используется та же элементная база, что и для привода постоянного тока: регуляторы на основе операционных усилителей, датчики тока, напряжения, аналоговые и импульсные датчики частоты вращения, преобразователи аналогового сигнала в импульсный, множительно-делительные устройства и др.

Рассмотрим структурную схему регулируемого электропривода с автономным инвертором тока (рис. 2). Выходной сигнал пропорционально-интегрального регулятора (ПИ-регулятора) скорости является заданием тягового усилия двигателя. При управлении с неизменным током статора машина приобретает неблагоприятные свойства, заключающиеся в том, что с увеличением нагрузки (скольжения) резко падает магнитный поток. Поэтому система должна быть замкнута так, чтобы с увеличением нагрузки по определенному закону и ток статора увеличивался бы таким образом, чтобы поток машины поддерживался постоянным.

Ток двигателя при всех частотах пропорционален скольжению. Сигнал, преобразованный в функциональном построителе, рассчитанном на основе полевого расчета двигателя [4], выполняет данное условие, т. е. является заданием амплитуды тока, которое отрабатывается замкнутой системой автоматического управления. Быстродействие в отработке задания тягового усилия будет определяться быстродействием системы регулирования амплитуды тока статора. Пользуясь результатами полевого расчета двигателя, мы сможем программировать элемент (блок формирования усилия на рис. 3), характеризующий усилия, возникающие в ЛАД ПП с учетом скольжения и магнитного зазора.

При синтезе контура тока задание амплитуды тока отрабатывается в замкнутой системе (рис. 4). В системе электропривода контур регулирования тока статора является внутренним. Результаты его настройки (рис. 5) во многом определяют быстродействие и качество регулирования синтезируемой системы. Объект регулирования является таким же, что и для автоматизированного при-

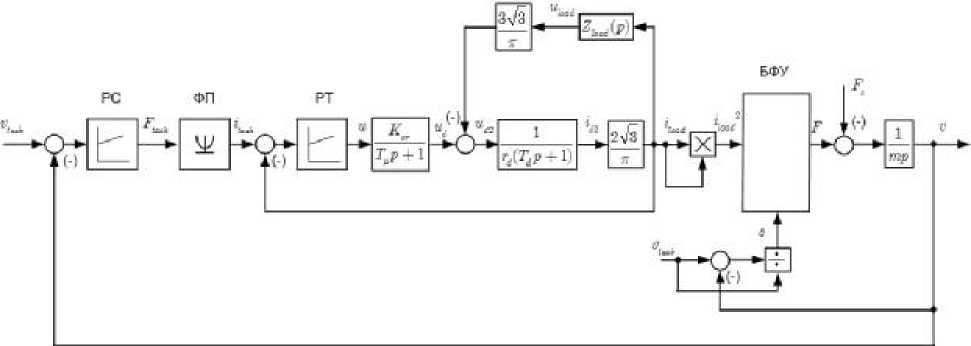
Рис. 2. Структурная схема регулируемого электропривода с автономным инвертором тока

основан метод непрерывной аппроксимации применительно к вентильным коммутаторам.

контура тока состоит из преобразователя с СИФУ, дросселя и автономного инвертора тока.

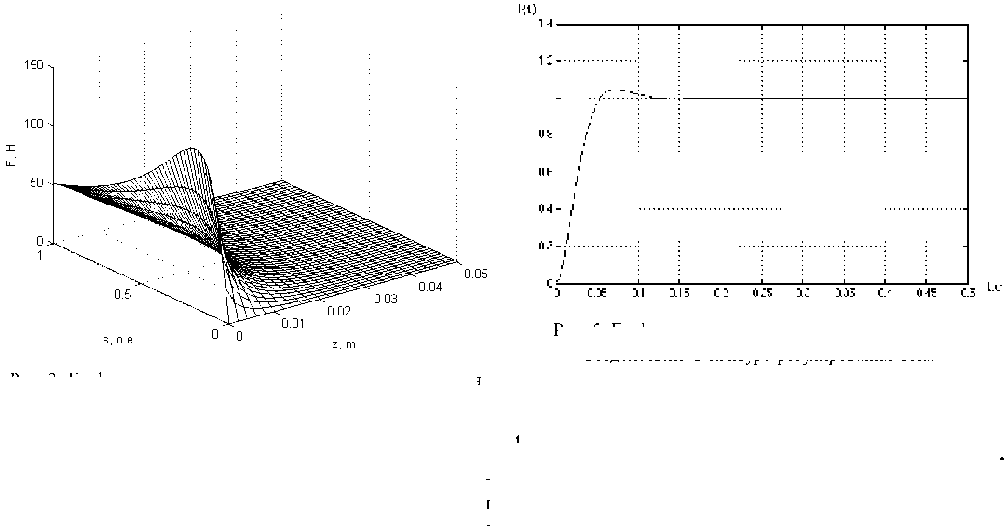
Рис. 3. График зависимости тягового усилия от скольжения и величины зазора между статором и вторичным элементом двигателя

Рис. 5. График переходного процесса по задающему воздействию в контуре регулирования тока

При синтее контура скорости на входе регулятора скорости сравниваются сигналы задания и обратной связи по скорости. Выходной сигнал этого регулятора является заданием тягового усилия двигателя. Блок ФПКТБФУ (рис. 6), состоящий из преобразователя частоты, двигателя, регулятора тока и звена, поддерживающего его потокосцепление постоянным, является устройством отработки задания по тяговому усилию. Эта отработка не может быть безынерционной, так как ФПКТБФУ включает инерционные силовые элементы, а также вентильные преобразователи, обладающие ограниченной частотой пропускания. Передаточную функцию ФПКТБФУ можно определить в виде апериодического звена

W ( P ) =

( T P + 1)

Таким образом, мы получили ПИ-регулятор скорости, параметры которого подбираются экспериментально (рис. 7).

При анализе влияния автономного инвертора на динамические характеристики системы инвертор целесообразно расчленить на вентильный коммутатор и устройство принудительной коммутации. При анализе влияния вентильного коммутатора в рассмотрение вводится

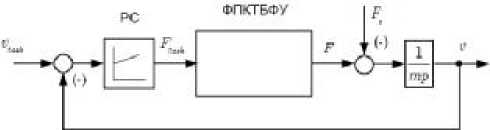
Рис. 6. Упрощенная структурная схема электропривода с регулятором скорости

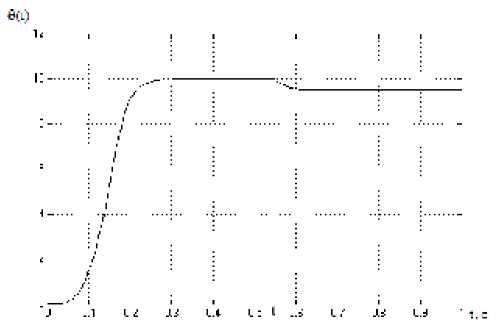
Рис. 7. График переходного процесса по задающему воздействию при пуске и при набросе нагрузки в контуре регулирования скорости в момент времени t ₁

Таким образом, входное напряжение автономного

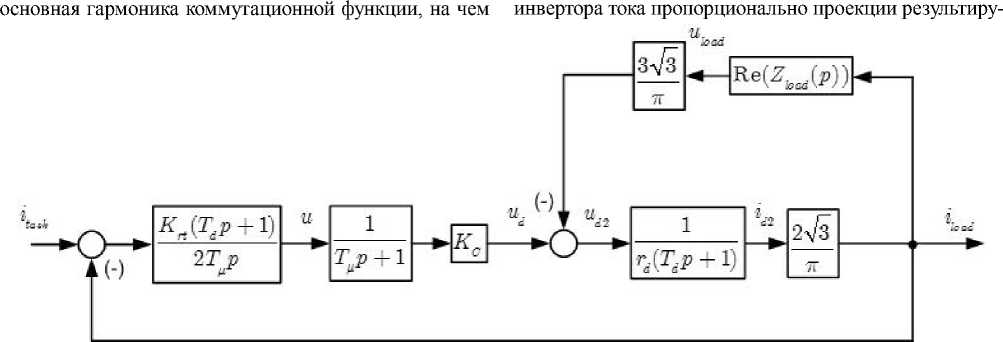
Рис. 4. Структурная схема контура регулирования тока

ющего вектора напряжения нагрузки на результирующий вектор тока. При линейной нагрузке и фиксированной выходной частоте ω автономный инвертор как элемент цепи постоянного тока может быть представлен в виде передаточной функции, которая для автономного инвертора тока пропорциональна действительной части операторного сопротивления нагрузки во вращающейся со скоростью ω системе координат.

При построении модели в пакете программ MatLAB используются программируемые блоки, значения которых получены при помощи полевого расчета многофазного ЛАД. Настройка контура регулирования тока производится по критерию модульного оптимума [5]. При единичном ступенчатом воздействии перерегулирование составляет 4,3 %. В контуре регулирования скорости используется ПИ-регулятор, параметры которого были определены экспериментально. Переходный процесс носит апериодический характер. В результате система является устойчивой к различного рода возмущающим воздействиям.