Исследование энергобаллистических характеристик вариантов марсианского пилотируемого экспедиционного комплекса для различных синодических периодов системы Земля-Марс

Различным аспектам марсианской пилотируемой экспедиции посвящено большое количество исследований [1–4]. Одной из научно-технических проблем, связанных с экспедицией на Марс, является выбор наиболее предпочтительного варианта энергодвигательного обеспечения. Среди рассматриваемых вариантов можно выделить имеющие наибольшую степень готовности — жидкостные ракетные двигатели (ЖРД), ядерные ракетные двигатели (ЯРД), ядерные электроракетные двигательные установки (ЯЭРДУ). Эти варианты энергодвигательного обеспечения имеют различные достоинства и недостатки и, с учётом неопределённости требований к характеристикам марсианской пилотируемой экспедиции, на сегодняшний день ни один из этих вариантов невозможно исключить из рассмотрения. Основные усилия исследователей направлены на поиски наиболее приемлемых (по различным показателям, например по продолжительности экспедиции и начальной массе) вариантов экспедиции.

Невозможность однозначного выбора типа энергодвигательного обеспечения, в частности, связана с отсутствием однозначности в выборе критерия эффективности. Даже энергобаллистические показатели эффективности (начальная масса марсианского экспедиционного комплекса — МЭК; продолжительность экспедиции) носят противоречивый характер. Имеющиеся возможности в выборе сценариев экспедиции (например, выбор баллистического варианта перелёта, выбор принципа спуска экипажа на поверхность Земли — с орбиты или прямой вход корабля возвращения в атмосферу, варианты подсадки экипажа) существенным образом влияют на показатели эффективности и, следовательно, усложняют процесс выбора предпочтительного варианта энергодвигательного обеспечения. Другим аспектом проблемы выбора являются прогнозный характер параметров и неодинаковая степень проработанности различных типов энергодвигательного обеспечения. Наконец, не определены требования к показателям эффективности, что делает проблематичным аргументацию в пользу того или иного варианта.

Одной из важных задач при выборе типа энергодвигательного комплекса (ЭДК) является обеспечение возможности регулярных (в каждый синодический период системы Земля–Марс) экспедиций. Литература по ЭДК на основе ЯЭРДУ часто является уже устаревшей, так как рассматриваются уже прошедшие даты, как, например, в работе [5]. Кроме того, на сегодняшний день достигнуты определённые успехи в сквозном моделировании марсианской экспедиции [6–8] (под этим понимается оптимизация сразу всех участков траектории экспедиции в рамках постановки единой задачи). Также относительно недавно сформулированы возможные варианты баллистических схем экспедиции [9, 10], классификация которых применима как для двигательных установок (ДУ) большой тяги, так и для ЯЭРДУ. Однако в работе [9] расчёт основных показателей экспедиции вёлся при помощи последовательного расчёта участков траектории экспедиции [при принятых упрощениях о постоянстве массы системы хранения и подачи рабочего тела (СХПРТ), а также фиксированной дате отлёта МЭК от Земли]. Возникает вопрос: сохраняются ли основные свойства баллистических схем при сквозной оптимизации траектории марсианской пилотируемой экспедиции (при определении массы СХПРТ пропорционально массе требуемого рабочего тела и оптимизации даты отлёта МЭК от Земли)?

Следует отметить, что широко распространено мнение о преимуществе в продолжительности экспедиции для ЭДК на базе ДУ большой тяги перед ЭДК с ДУ на базе ЭРДУ. Такое мнение сформировано часто применяемым подходом, когда для вариантов экспедиции с ДУ большой тяги рассматривается схема с прямым входом корабля возвращения экипажа на Землю (КВЗ) в атмосферу Земли, а для вариантов экспедиции с ЯЭРДУ — возвращение с выходом на орбиту базирования. Из-за такого различия сценариев экспедиции требуется рассмотрение сравниваемых вариантов ЭДК в одинаковых условиях (с прямым входом КВЗ в атмосферу Земли).

Исходные данные и основные методические положения

Исходные данные по характеристикам составляющих МЭК близки к принятым в работах [9–11].

В расчётах, проведённых в рамках настоящей работы, рассматривались варианты ЭДК марсианской пилотируемой экспедиции на базе ЯЭРДУ, которые сравнивались с ЭДК на базе ЖРД и ЯРД.

Полагалось, что МЭК включает в себя взлётно-посадочный комплекс (ВПК) массой 40 т для ЯЭРДУ и 55 т — для ЖРД и ЯРД; КВЗ массой 16,5 т; орбитальный модуль массой 60 т, а также ЭДК, масса которого существенно зависит от его типа.

Высота стартовой орбиты (и орбиты возвращения) у Земли — 1 000 км. В случае возвращения с прямым входом КВЗ в атмосферу Земли высота атмосферы полагалась равной 100 км, а ограничение на скорость входа КВЗ в атмосферу — не более 12,5 км/с.

Высота орбиты ожидания у Марса — 400 км (в случае применения ЖРД или ЯРД рассматривалась эллиптическая орбита 20 000/400 км).

В случае применения кислородноводородных ЖРД на первой ступени для разгона у Земли масса первой ступени определялась прямо пропорционально массе топлива с коэффициентом 0,13. На второй, третьей и четвёртой (если требуется торможение у Земли) ступенях также рассматривался вариант кислородноводородного ЖРД (коэффициент 0,15). Удельный импульс ЖРД на криогенных компонентах принимался равным 470 с.

Масса ЭДК на базе ЯРД складывалась из массы ЯРД (55 т) и массы водородных баков (вычислялась прямо пропорционально израсходованному рабочему телу с коэффициентом 0,23). Удельный импульс тяги ЯРД полагался равным 900 с.

Масса энергодвигательного комплекса mЭДК на базе ЯЭРДУ определялась согласно зависимости mЭДК = αСХПРТ mт + NЯЭРДУγЯЭРДУ через электрическую мощность ЯЭРДУ NЯЭРДУ и удельную массу ЭДК γЯЭРДУ без баков (предполагалось, что масса системы хранения и подачи рабочего тела прямо пропорциональна массе рабочего тела mт с коэффициентом пропорциональности αСХПРТ = 0,05). Мощность ЯЭРДУ полагалась равной 25 МВт, а удельная масса ЭДК — 10 кг/кВт. Таким образом, масса энергодвигательного обеспечения на базе ЯЭРДУ без СХПРТ составляла 250 т.

Удельный импульс тяги для ЯЭРДУ принимался равным 7 000 с (за исключением отдельно рассмотренных случаев, где он варьировался); коэффициент полезного действия (КПД) системы преобразования и управления ЭРДУ — 0,95; тяговый КПД ЭРДУ — 0,70.

Даты отлёта для вариантов ЯЭРДУ оптимизировались в каждом синодическом периоде интервала 2049–2072 гг.

Продолжительность пребывания МЭК на орбите Марса ∆ t _ож принималась постоянной и равной 30 сут или оптимизировалась (для схемы с длительным ожиданием МЭК на орбите около Марса).

Во всех расчётах настоящей работы эфемериды планет рассчитывались с использованием модели EPM2008 [12].

Методический подход к расчёту основных характеристик марсианской пилотируемой экспедиции

Методический подход к расчёту энергобаллистических показателей эффективности марсианской пилотируемой экспедиции базировался на сквозных расчётах траектории перелёта Земля–Марс–Земля. Оптимизационная задача перелёта Земля–Марс–Земля пилотируемой экспедиции на Марс может быть сформулирована как задача расчёта связанных гелиоцентрических участков с разрывом фазовых переменных вблизи Марса и краевыми условиями на околоземные участки. Основные методические положения приведены ниже. Для удобства расчётов вся экспедиция делилась на следующие этапы полёта (моделирование каждого из которых может быть с достаточной точностью проведено в рамках ограниченной задачи двух тел). Принятая нотация (обозначения номеров участков и индексов переменных) приведена в таблице.

Принятые обозначения и нумерация этапов экспедиции

Номер участка траектории	1	2	3	4	5	6	7
Этап полёта	Разгон около Земли	Перелёт Земля–Марс	Скрутка у Марса	Орбитально-десантная операция	Раскрутка у Марса	Перелёт Марс–Земля	Скрутка у Земли
Обозначения моментов времени	00	t 0	t 1 t –	t 2	t 3	t 4 t +	t 5           t 6
Центральное тело	Земля	Солнце	Марс	Марс	Марс	Солнце	Земля

Характеристики припланетных участков могут быть довольно точно оценены с использованием зависимости из работы [13]. Ввиду симметрии можно считать затраты топлива на скрутку и раскрутку равными.

1 – ti – ti – 1 =

– 0,8209 4 ai 2/2Vуд tхарi a i

t;

хар mi = mi – 1

1 – 0,8209 ⁴ a_i – 1 – 0,8209 ⁴ a_i ² /2 V _уд

V уд где ti — безразмерная продолжительность (i + 1)-го участка раскрутки/скрутки; ai — безразмерное начальное ускорение; Vуд — безразмерная скорость истечения реактивной струи; tхарi и tхар — характерные времена (i + 1)-го участка (припланетного) и гелиоцентрического соответственно; mi и mi – 1 — безразмерные массы в конце и начале (i + 1)-го участка раскрутки/скрутки соответственно. Можно ввести следующие обозначения:

f_ti = t_i – t_{i – 1} ;

^f mi ⁼ m i ^/ m i – 1 ^.

Методика моделирования межпланетного перелёта предполагала использование метода грависфер нулевой протяжённости [14]. При этом полагалось, что припланетные участки раскрутки обеспечивают нулевой гиперболический избыток скорости. Для участков скрутки начальные условия также полагались соответствующими движению по параболе. Таким образом, краевые условия на гелиоцентрических участках в основном состояли в совпадении соответствующих координат аппарата и планеты старта и назначения.

Наиболее простая запись постановки краевой задачи получается с использованием декартовой системы координат. Для перевода координат и сопряжённых в другие системы координат могут использоваться канонические преобразования [15, 16].

Уравнения движения

R ^. = V ;

.R

V = –   + a δ;

R ³

m. = – δ, где R и R — радиус-вектор МЭК и модуль этого вектора (здесь и далее векторы обозначены полужирным начертанием, а их модули — светлым начертанием); V — вектор скорости МЭК; a — ускорение, обеспечиваемое ДУ; δ — функция включения/выключения ДУ (1 — ДУ включена, 0 — ДУ выключена); m и — масса и задаваемый массовый расход ДУ соответственно. Формально уравнения движения могут быть дополнены уравнениями для полётного времени t и даты отлёта от

Земли t ₀ . Далее и t , и t ₀ рассматриваются как обычные переменные, что обеспечивает возможности использования стандартных постановок принципа максимума [17]. .

t = 1;

t ^. ₀ = 0.

Гамильтониан

H = p_RV + p_V

– ^R + a

R ³

– p_m δ + p_t + p_{t 0} ,

где p_R , p_V , p_m , p_t и p_{t 0} — соответствующие сопряжённые переменные.

Ускорение может быть выражено через тягу ДУ R _д :

R

a = ^д b ,

m

где b — единичный вектор, задающий направление вектора тяги.

Управление (из принципа максимума):

p V b = _{p V} ;

(1, если А > 0;

0, если А < 0;

R

∆ = p ^д – p , V m m ^,

где ∆ — функция переключения; p_V — модуль вектора сопряжённых скорости.

Направление тяги b определяется углами α и γ между вектором тяги, опорной плоскостью и опорным направлением в опорной плоскости соответственно. Таким образом, в задаче присутствуют три переменных управления — α, γ и δ.

Сопряжённые уравнения:

.

^p R

^{p V} – 3 R

R ³

pVR

R ⁵

p_V = – p_R ;

.R p = – д δp b;

m     m2   V p.t = 0;

p ^. _{t 0} = 0.

Дифференциальные уравнения движения и им сопряжённые интегрировались численно с применением метода Рунге–Кутта–Фельберга 7(8)-го порядка [18, 19].

Минимизируемым функционалом J системы выбрана продолжительность экспедиции T (включая гелиоцентрические участки перелёта Земля–Марс и Марс–Земля, а также припланетные участки), J = T .

Начальная масса МЭК при этом фиксировалась (а в дальнейших расчётах её величина параметрировалась).

Минимизируемый функционал — продолжительность экспедиции — может быть записан различными выражениями. Для дальнейшего анализа рассматривалась следующая форма:

J = t + f_{t 6}

при ограничении

G = m(t00) – m00 = 0, где m00 — заданное значение начальной массы МЭК.

Краевые условия на левом конце гелиоцентрического участка траектории Земля–Марс–Земля (в момент t ₀ принималось t = 0) состояли из следующих выражений:

g01…3 0 g4…6 . g0 у = 'R - Rз(tо + t) V — Vз( 10 + t) 4 m - m00 fm0 J = 0, (1) где RЗ и VЗ — радиус-вектор и вектор скорости Земли соответственно.

Краевые условия (1) отражают совпадение координат и скоростей МЭК и Земли в начале гелиоцентрического участка. Фазовые координаты Земли определяются из эфемеридной модели EPM2008 . Условие (1) дополнено условием непрерывности массы МЭК после раскрутки и в начале гелиоцентрического участка перелёта Земля–Марс.

Краевые условия на правом конце гелиоцентрического участка траектории Земля–Марс–Земля (в момент t = t ₅ ) фиксированы положением планеты назначения.

^{к g} 1…3

g

к

4…6

g ^к ₇

R – R _З ( t ₀ + t ₅ )

V – V _З ( t ₀ + t ₅ )

m 5 ^fm 6 ^{(1 + а} СХПРТ )   m const   ⁽ m 00

m впк ^{) а} схпрт

= 0,

где m ^к _const — возвращаемая масса МЭК за исключением СХПРТ, состоящая из масс ЭДК (без баков), КВЗ и ОМ; m _ВПК — масса взлётно-посадочного комплекса.

Последнее условие получается из равенства для конечной массы по расчётам и согласно заданной модели:

m 6 ⁼ m 5 ^f m 6 ⁼ m ^к const ⁺ α СХПРТ m т ^{∑ ,} где m _т ^∑ — суммарная масса рабочего тела.

Как уже было упомянуто выше, характеристики участков 3 , 4 и 5 (см. таблицу) рассчитывались с применением аналитических зависимостей из работы [13]. При переходе от полётного времени t к другой независимой переменной эти участки моделировались как мгновенное (по независимой переменной) изменение фазовых переменных (разрыв фазовых переменных, включая переменную t ) в соответствии со сформулированными ниже условиями.

^{g ±}1…3

^g 4…6

^g 7…9

^g 10…12

^g 13

R ^– – R _M ( t ₀ ^– + t^– )

V ^– – V M ( t 0 ^– + t^– )

R ⁺ – R M ( t⁺ 0 + t⁺ )

V ⁺ – V M ( t⁺ 0 + t⁺ )

m⁺ – ( m^–f_{m 2} – m _ВПК ) f_{m 4}

g ±4        t + ^{- t — — Д} t ож ^{— f — f} 4

= 0,

g±15 t0+ – t0– где индексами «+» и «–» обозначено соответствие значений переменных в моменты t+ и t–; RM и VM — радиус-вектор и вектор скорости Марса соответственно.

Из условий трансверсальности можно получить выражение для сопряжённой массы после разрыва фазовых переменных:

p_m ⁺

.

p^- + ( P r ^{V -} + P v ^{V - -} ^ ^{S -} p m ^- P r ^V m

.

– p_V ^– V _M ^– )

' 8f t 2 + f 8 m ^-   8 m ^- ₇

: ^{8 [(} m ^f m 2 ^- m ВПК ) ^f m 4 ^] 8 m ^-

Условие для определения момента разрыва фазовых переменных:

....

pR– (V– – VM–) + pV– (V – – V M–) – pR+ (V+ – VM+) – pV+ (V + – V M+) – (δ–pm– – δ+pm+) = 0.(4)

Из условий трансверсальности можно получить выражение для определения даты отлёта от Земли t ₀ :

.    ...

pR(0)VЗ(t0) + pV(0)V З(t0) – pR–VM– – pV– V M– + pR+VM+ + pV+ V M+ – pR(t5)VЗ(t0 + t5) – pV(t5)V З(t0 + t5) = 0.(5)

Неизвестные краевой задачи (15 переменных):

p_R (0), γ(0), α(0), p_m (0), p_R ⁺ , p_V ⁺ , t ₅ , t ₁ , t ₀ .

Сопряжённые скорости p_V находятся через углы ориентации тяги γ(0) и α(0), что является известным приёмом нормировки сопряжённых переменных:

p_Vx (0) = cos[γ(0)] cos[α(0)];

p_Vy (0) = sin[γ(0)] cos[α(0)];

p_Vz (0) =sin[α(0)].

Составляющие невязки определяют выражения (1), (2), (4), (5).

Решение поставленной краевой задачи осуществлялось с использованием методов градиентного спуска и Ньютона [13].

Методики сквозного расчёта перелёта Земля–Марс–Земля встречаются в научно-технической литературе, например в работах [6–8]. При этом наиболее полное описание постановки задачи и необходимых условий оптимальности приведено в работе [8].

Выражение (3), определяющее p_m ⁺ , а также условия (4) и (5) для определения момента разрыва фазовых переменных и даты отлёта МЭК от Земли, могут быть приведены к форме соответствующих математических выражений, представленных в работе [8], при условии совпадения моделей гравитационных полей в системе дифференциальных уравнений движения и модели эфемерид. В рассматриваемом в данной работе случае, как и в работе [8], уравнения движения описывают простейший случай центрального (ньютоновского)

гравитационного поля, в то время как используемые эфемериды EPM2008 (в работе [8] эфемеридная модель не указана) учитывают большое количество отличий гравитационного поля от центрального. Дополнительным отличием методики из работы [8] является встроенная в краевую задачу оптимизация удельного импульса тяги. В методике настоящей работы удельный импульс тяги принимается постоянным (параметрируется) и является частью исходных данных для расчётов.

Для варианта с непрерывной работой ДУ на участке Земля–Марс в краевой задаче неизвестная p_m (0) исключается из рассмотрения (δ = 1 из принципа максимума [20]), а вместо неё рассматривается неизвестная m ₀₀ . Остальной состав неизвестных краевой задачи в случае непрерывной работы ЭРДУ не меняется (15 переменных). Состав невязки, по сравнению с предыдущей постановкой краевой задачи, также остаётся неизменным.

В случае прямого входа КВЗ (с ограничением на величину гиперболич е ского избытка скорости V _∞ не более V _∞ ) на этапе возвращения вместо ограничений g ₄ ^к _…6 в момент t ₅ может быть записано следующее ограничение:

g ₄ ^к = V _∞ – V _∞ cos ² ξ = 0,                 (6)

где V _∞ =

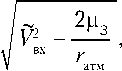
здесь тил ь дой отмечены задаваемые значения, V _вх — заданный уровень скорости входа КВЗ в атмосферу Земли; V _∞ — соответствующий заданному уровню скорости входа КВЗ в атмосферу

Земли гиперболический избыток скорости; ξ — дополнительная переменная для автоматического определения (из решения краевой задачи) выхода или невыхода на ограничение по скорости входа в атмосферу Земли; µ _З — гравитационный параметр Земли; r _атм — радиус атмосферы Земли (принят соответствующим высоте 100 км).

Из условий трансверсальности можно получить следующее модифицированное условие для определения даты отлёта МЭК от Земли, вместо выражения (5):

..

p R (0) V З ( t 0 ) + p V (0) V З ( t 0 ) – p R ^– V M ^– – p V ^– V M ^– +

.

+ p_R ⁺ V _M ⁺ + p_V ⁺ V _M ⁺ – p_R ( t ₅ ) V _З ( t ₀ + t ₅ ) –

– ν ₄ ^к

*

V З х ( 1 0 + 1 5 ) [ V x ( 1 5 ) — V З х ( 1 0 + 1 5 )] ² +

< ^{+ V} 3 y ( 1 0 ⁺ 1 5 ) [ V y ( 1 5 ) — ^V З у ( 1 0 ⁺ 1 5 )] 2 ⁺ >

*

I^{+ V} 3 z ( 1 0 ⁺ 1 5 ) [ ^V z ( 1 5 ) — ^V 3 z ( 1 0 ⁺ 1 5 )] 2    J

V .

= 0,

где индексами x , y и z обозначены проекции векторов на соответствующие оси декартовой системы координат.

Неизвестные краевой задачи увеличиваются до 17 переменных (дополнительные переменные — ν ₄ ^к и ξ).

В составе невязки краевое условие g4к…6 = V – VЗ(t0 + t) = 0

заменяется на уравнение pV

V ( 1 5 ) — V з ( 1 0 + 1 5 )

V ∞

Также появляются две дополнительные компоненты невязки — выражение (6) и ν ₄ ^к sinξ = 0.

Остальные компоненты невязки и неизвестные краевой задачи остаются неизменными, как и при возвращении МЭК на орбиту базирования у Земли.

Применительно к случаю c непрерывно включённой ЭРДУ и прямым входом КВЗ в атмосферу Земли постановка задачи изменяется аналогично случаю возвращения КВЗ на околоземную орбиту.

Рассмотрение задачи с длительным ожиданием отличается от рассмотренных выше постановок появлением    дополнительной перемен ной ∆tож.

Условие (5) для определения даты отлёта распадается на два выражения (входят в состав невязки; размерность краевой задачи увеличивается на единицу):

..

p R (0) V З ( t 0 ) + p V (0) V З ( t 0 ) – p R ^– V M ^– – p V ^– V M ^– = 0;

.

p_R ⁺ V _M ⁺ + p_V ⁺ V _M ⁺ – p_R ( t ₅ ) V _З ( t ₀ + t ₅ ) –

.

– p_V ( t ₅ ) V _З ( t ₀ + t ₅ ) = 0.

В случае прямого входа КВЗ в атмосферу Земли последнее выражение принимает следующий вид:

.

p_R ⁺ V _M ⁺ + p_V ⁺ V _M ⁺ – p_R ( t ₅ ) V _З ( t ₀ + t ₅ ) –

.

[ V x ( 1 5 ) — V З х ( 1 0 + 1 5 )] V З х ( 1 0 + 1 5 ) +

.

' ⁺ [ ^Vy ( t 5 ) — ^V 3 y ( t 0 ⁺ t 5 )] ^V 3 y ( t 0 ⁺ t 5 ) ⁺ >

.

[ + [ У ( 1 5 ) - V 3 z ( 1 0 + 1 5 )] V 3^ ( 1 0 + 1 5 )      J

Остальные компоненты невязки и неизвестные краевых задач остаются неизменными.

Следует заметить, что вариант непрерывно включённой ЭРДУ применительно к задаче с длительным ожиданием у Марса теряет связь с задачей быстродействия. В этом случае минимизируемым функционалом является начальная масса МЭК.

Исследование энергобаллистических характеристик марсианской пилотируемой экспедиции

Проведённые в ходе исследования расчёты были направлены на оценку начальной массы МЭК и продолжительности экспедиции. Вопросы, связанные с реализацией полученных в ходе оптимизации траекторий (например, потребность в малых корректирующих манёврах на длительных участках перелёта) требуют отдельного анализа.

Показатели энергомассовой эффективности (начальная масса МЭК, продолжительность экспедиции) оце- нивались применительно к следующим баллистическим схемам пилотируемой экспедиции [9, 10]. Две схемы с непродолжительным пребыванием МЭК около Марса (30 сут) — класс А (схема характеризуется приближением к Солнцу ближе границ орбиты Земли, т. е. расстояние до Солнца в процессе полёта сокращается до значений менее 1 а. е.) и класс В (схема без приближения к Солнцу), а также схема с длительным ожиданием (пребыванием) МЭК на орбите около Марса (до 600 сут и более). Указанные схемы не только являются семействами экстремалей для ЭДК на базе ЯЭРДУ, но и соответствуют траекториям с минимальным набором характеристической скорости применительно к ЭДК на базе ДУ большой тяги [9, 10].

Целесообразность использования той или иной баллистической схемы должна быть увязана с целями экспедиции и требует всестороннего (не только проектно-баллистического) анализа.

Результаты оценок энергомассовых показателей эффективности (начальной массы МЭК, продолжительности экспедиции) для различных удельных импульсов тяги ЯЭРДУ в синодический период великого противостояния 2049–2050 гг. приведены на рис. 1. Рассматривается схема спуска экипажа на Землю с орбиты Земли со скоростью входа КВЗ в атмосферу Земли ~8 км/с (МЭК возвращается на орбиту базирования, после чего осуществляются отделение КВЗ и возвращение экипажа на Землю).

Применительно к схеме экспедиции с приближением к Солнцу (класс А ) показаны начальная масса МЭК и продолжительность экспедиции для семейств экстремалей, реализующих приближение к Солнцу на этапе возвращения (гелиоцентрический участок траектории Марс–Земля) и на начальном этапе перелёта (гелиоцентрический участок траектории Земля–Марс). Последнее семейство экстремалей отличается от первого датой отлёта приблизительно на один год, поэтому далее подобные семейства именуются как «траектории класса А , дополнительная дата отлёта». Даты отлёта семейств класса А , В и длительного ожидания оказываются близкими (исключение составляет класс А , дополнительная дата отлёта).

Как видно на рис. 1, траектории обоих семейств класса А обеспечивают практически совпадающие показатели энергобаллистической эффективности.

Зависимости на рис. 1 и им подобные ниже построены наращиванием пассивных участков из точек с непрерывно включённой ЯЭРДУ (самые верхние точки каждого из семейств). Из рис. 1 могут быть построены огибающие зависимости, соответствующие оптимальному удельному импульсу тяги, для каждого из семейств экстремалей.

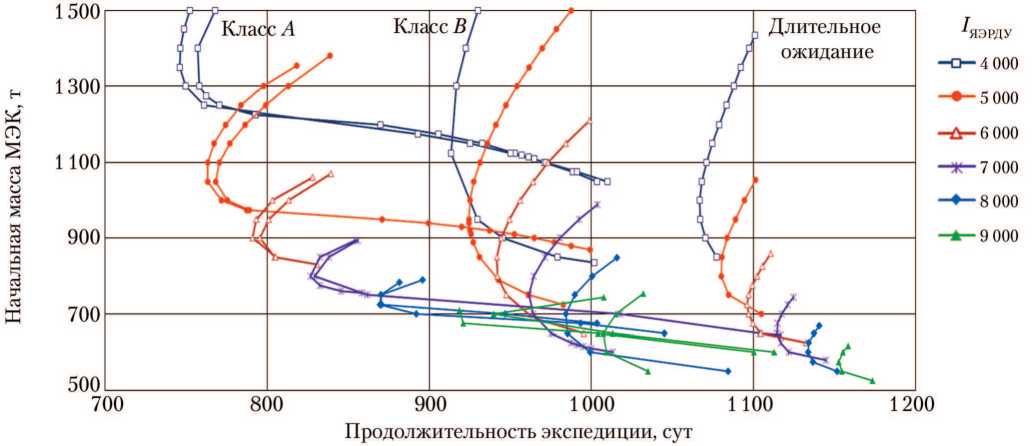
Рис. 1. Зависимость начальной массы марсианского экспедиционного комплекса (МЭК) от продолжительности экспедиции для различных удельных импульсов тяги ядерной электроракетной двигательной установки. Даты отлёта в синодический период 2049–2050 гг. (рисунок создан автором)

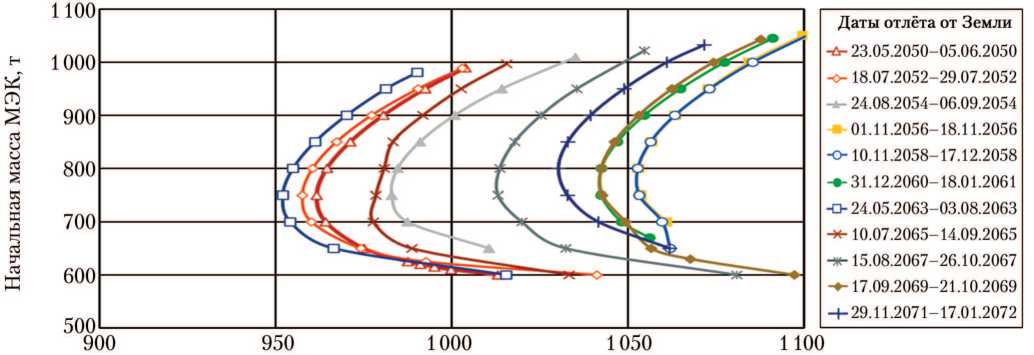
На рис. 2–5 приведены зависимости начальной массы МЭК от продолжительности экспедиции в оптимальные даты синодических периодов системы Земля–Марс за интервал 2049–2072 гг. применительно к траекториям классов А

(отдельный рис. 3 для дополнительной даты отлёта) и В , а также для длительного ожидания (пребывания) МЭК на орбите около Марса. Зависимости построены для удельного импульса тяги ЯЭРДУ 7 000 с.

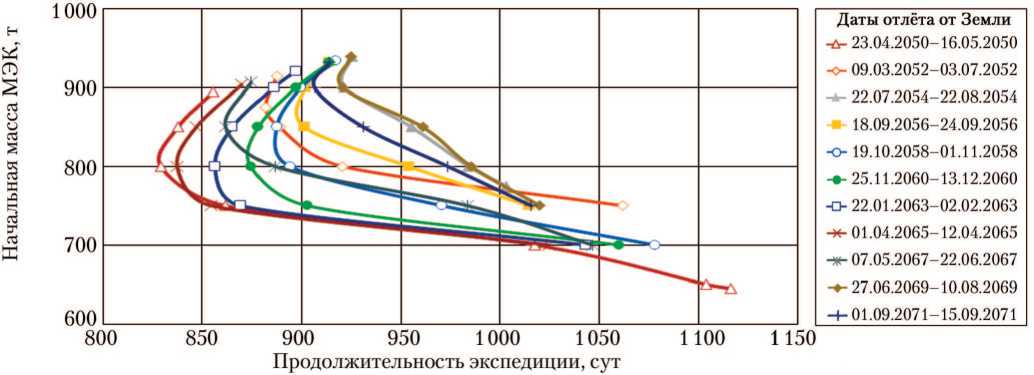
Рис. 2. Зависимость начальной массы марсианского экспедиционного комплекса (МЭК) от продолжительности экспедиции. Класс А (рисунок создан автором)

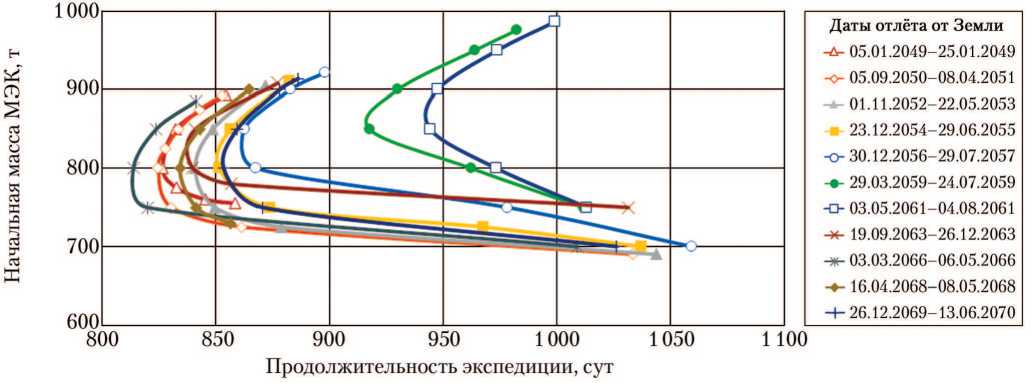
от продолжительности

Рис. 3. Зависимость начальной массы марсианского экспедиционного комплекса (МЭК) экспедиции. Класс А, дополнительная дата отлёта (рисунок создан автором)

Продолжительность экспедиции, сут

Рис. 4. Зависимость начальной массы марсианского экспедиционного комплекса (МЭК) от продолжительности

экспедиции. Класс B (рисунок создан автором)

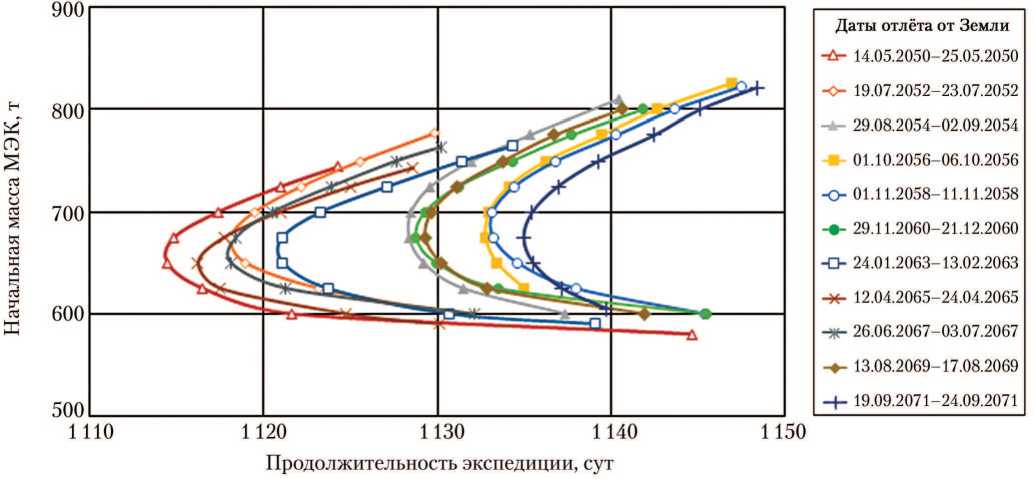
Рис. 5. Зависимость начальной массы марсианского экспедиционного комплекса (МЭК) от продолжительности экспедиции. Длительное ожидание у Марса (рисунок создан автором)

На рис. 2 и 3 можно отметить сохраняющееся во все синодические периоды рассмотренного интервала совпадение приведённых зависимостей класса А для основной и дополнительной дат отлёта МЭК от Земли.

Как видно на рис. 2–5, соответст- вующие рассматриваемым экстремалям интервалы начальной массы МЭК не претерпевают значительных изменений при переходе к другому синодическому периоду, а продолжительность экспедиции в неблагоприятные синодические периоды по сравнению с благоприятными увеличивается на величину вплоть до 180 сут для экстремалей класса А. Для экстремалей класса В это увеличение не превышает 100 сут, а при длительном ожидании (пребывании) МЭК на орбите около Марса — не превышает 20 сут.

Как следует из рис. 2–5, наилуч- шим синодическим периодом можно считать период великого противостояния Земли и Марса, например 2050–2052 гг., а наихудшим, например, синодический период 2058–2059 гг. Неожиданной оказалось применимость сделанного вывода для экстремалей с длительным ожиданием, так как применительно к ДУ большой тяги для экспедиций с длительным ожиданием годá великого противостояния, наоборот, являются неблагоприятными [10].

Как показывают результаты расчётов, в отдельные синодические периоды в рамках одного класса экстремалей (например, А или В) имеется неединственность решений, связанная с наличием экстремалей с участками траекторий Земля–Марс первого и второго полувитков [14]. При этом даты отлёта в этих решениях несколько отличаются. Примечательно, что в отличие от ДУ большой тяги, когда имеются оптимумы по затратам характеристической скорости, соответствующие как траекториям первого, так и второго полувитка, для варианта использования ЯЭРДУ такого рода неединственность решений появлялась лишь в отдельные синодические периоды, а не в каждом.

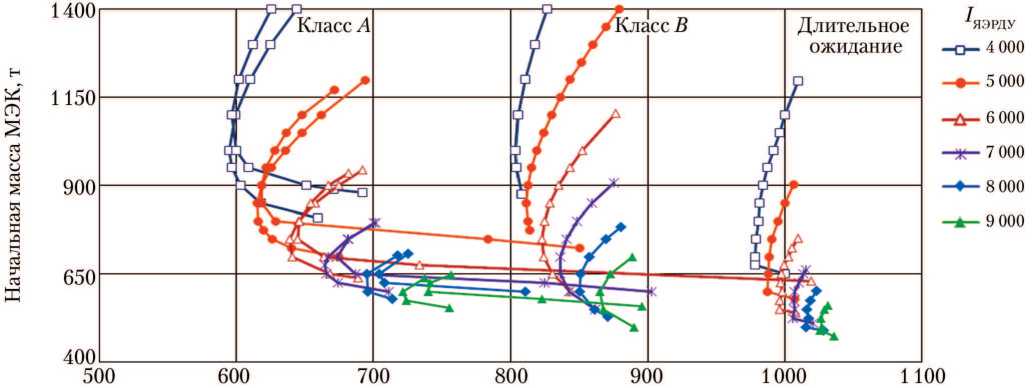
Исследования, аналогичные проведённым применительно к варианту возвращения экипажа на Землю с орбиты со скоростью входа КВЗ в атмосферу Земли ~8 км/с, были проведены для варианта, когда МЭК не выходит на околоземную орбиту, а спуск выполняется за счёт заблаговременного отделения КВЗ и его прямого входа в атмосферу со скоростью, не превышающей 12,5 км/с (последняя величина рассматривалась как ограничение, обеспечиваемое работой ЯЭРДУ на гелиоцентрическом участке Марс–Земля). Результаты этих исследований в виде зависимостей начальной массы МЭК от продолжительности экспедиции приведены на рис. 6–10.

Продолжительность экспедиции, сут

Рис. 6. Зависимость начальной массы марсианского экспедиционного комплекса (МЭК) от продолжительности экспедиции для различных удельных импульсов тяги ядерной электроракетной двигательной установки. Даты отлёта в синодический период 2049–2050 гг. Прямой вход корабля возвращения экипажа на Землю в атмосферу Земли со скоростью не более 12,5 км/с (рисунок создан автором)

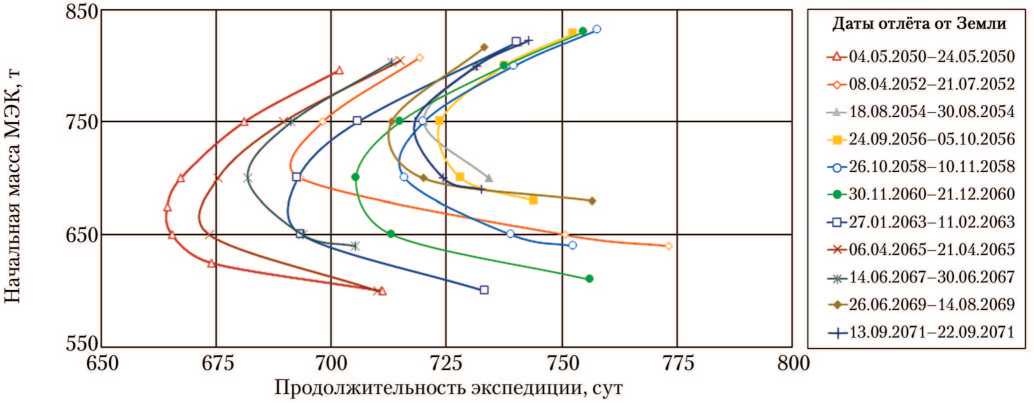
Рис. 7. Зависимость начальной массы марсианского экспедиционного экспедиции. Класс А. Прямой вход корабля возвращения экипажа на не более 12,5 км/с (рисунок создан автором)

комплекса (МЭК) от продолжительности Землю в атмосферу Земли со скоростью

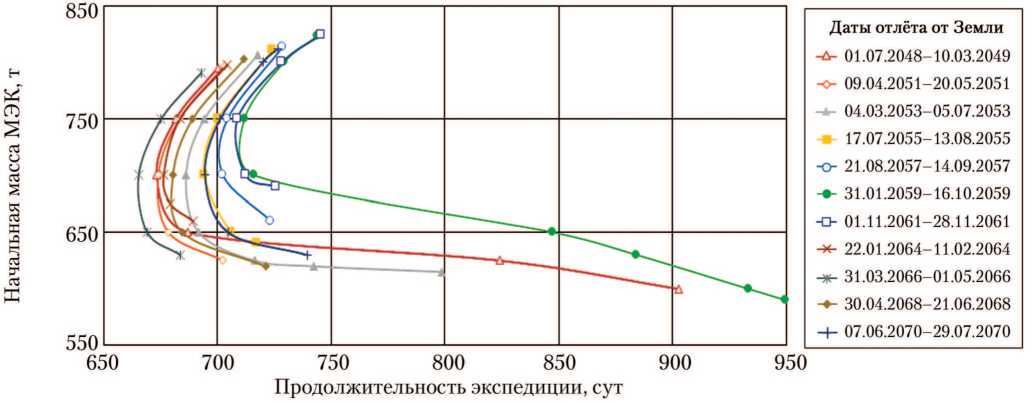
Рис. 8. Зависимость начальной массы марсианского экспедиционного комплекса

(МЭК) от продолжительности экспедиции. Класс А, дополнительная дата отлёта. Прямой вход корабля возвращения экипажа на Землю в атмо-

сферу Земли со скоростью не более 12,5 км/с (рисунок создан автором)

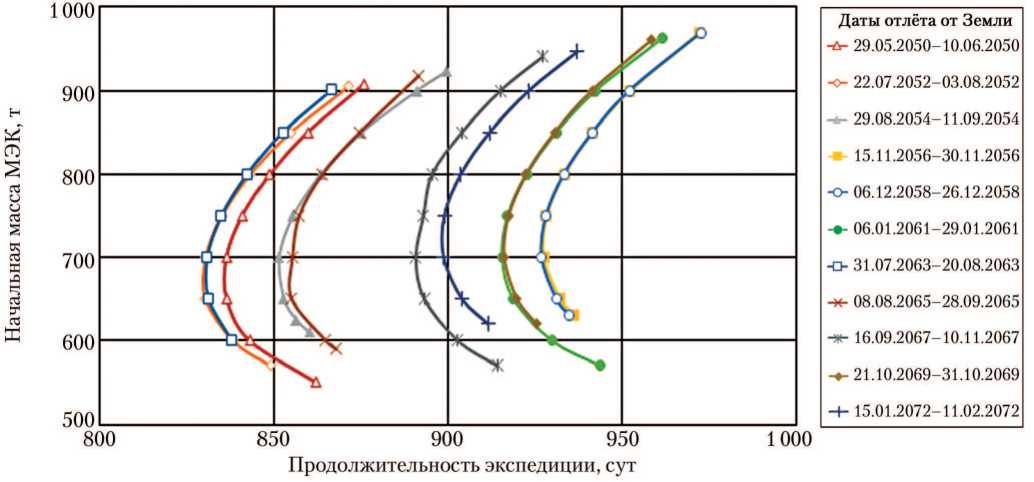
Рис. 9. Зависимость начальной массы марсианского экспедиционного комплекса (МЭК) от продолжительности экспедиции. Класс В. Прямой вход корабля возвращения экипажа на Землю в атмосферу Земли со скоростью не более 12,5 км/с (рисунок создан автором)

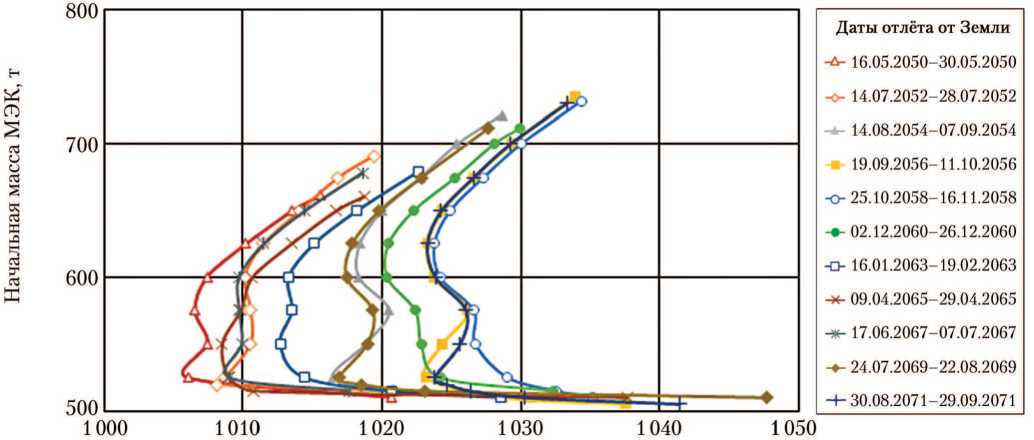
Продолжительность экспедиции, сут

Рис. 10. Зависимость начальной массы марсианского экспедиционного комплекса (МЭК) от продолжительности экспедиции. Длительное ожидание у Марса. Прямой вход корабля возвращения экипажа на Землю в атмосферу Земли со скоростью не более 12,5 км/с (рисунок создан автором)

Как видно на рис. 6–10, практически все выводы, сделанные для варианта спуска экипажа с орбиты со скоростью входа КВЗ в атмосферу Земли ~8 км/с, сохраняют справедливость и в случае прямого входа КВЗ в атмосферу Земли со скоростью не более 12,5 км/с. Ещё одним неожиданным результатом оказалось наличие экстремалей класса А с дополнительной датой отлёта — изначально представлялось, что прямой вход в атмосферу приведёт к исчезновению этого семейства экстремалей или существенному ухудшению показа- телей энергобаллистической эффективности, позволяющему исключить это семейство экстремалей из рассмотрения.

Представляет интерес изменение характера зависимостей на рис. 10 для семейства экстремалей с длительным ожиданием (пребыванием) МЭК на околомарсианской орбите. Возможно, такой характер объясняется наличием неединственности решений, связанным как с имеющимися экстремалями с выходом на ограничение по скорости входа КВЗ в атмосферу Земли и экстремалями, у которых это ограничение выполняется без выхода на его границу (скорость входа меньше 12,5 км/с), так и с наличием семейств экстремалей, отличающихся знаком множителя Лагранжа ν4к. Найденные в отдельных точках подобные экстремали, демонстрирующие неединственность решений, не всегда находятся в других точках. Объяснение поведения зависимостей на рис. 10 требует дальнейших исследований.

Сравнение вариантов МЭК на основе энергодвигательного обеспечения различных типов

Рассматривается схема посадки экипажа на Землю по прямой схеме со скоростью входа КВЗ в атмосферу Земли не более 12,5 км/с. Варианты МЭК с ЭДК на базе ЖРД и ЯРД не способны обеспечить выход на орбиту со сколько-нибудь разумными начальными массами МЭК, что является следствием недостаточно высокого удельного импульса тяги ДУ данных типов для энергозатрат перелёта Земля–Марс–Земля. Предполагалось, что в случае потребности погасить скорость для обеспечения заданного ограничения скорости входа КВЗ в атмосферу Земли не более 12,5 км/с, включение ДУ осуществляется на границе грависферы Земли. Следует заметить, что с точки зрения энергозатрат этот вариант является наиболее тяжёлым, в сравнении с торможением на подлёте к Земле на более близких расстояниях. Однако в предельном случае торможения на границе атмосферы (именно такой случай рассмотрен в работе [10]), хотя энергомассовые показатели существенно улучшаются (например, при приемлемой начальной массе МЭК становятся возможны «быстрые» экспедиции по траекториям класса А продолжительностью 430–500 сут), остро встают проблемы быстродействия и точности работы ДУ и системы управления, увеличиваются риски, а для варианта ЯРД — проблемы радиационной безопасности. В варианте ЯЭРДУ таких проблем не возникает, так как ограничение на скорость входа отрабатывается на гелиоцентрическом участке.

Применительно к синодическому периоду великого противостояния 2049–2050 гг. на рис. 11 показаны зависимости начальной массы МЭК от продолжительности экспедиции для ЭДК с ДУ на базе ЖРД, ЯРД и ЯЭРДУ. Рассматривались экстремали семейств класса А , класса В и длительного ожидания (пребывания) МЭК на орбите около Марса. Применительно к МЭК с ЯЭРДУ зависимости на рис. 11 представляют собой огибающую кривую (см. рис. 6) при оптимальном удельном импульсе тяги ЯЭРДУ.

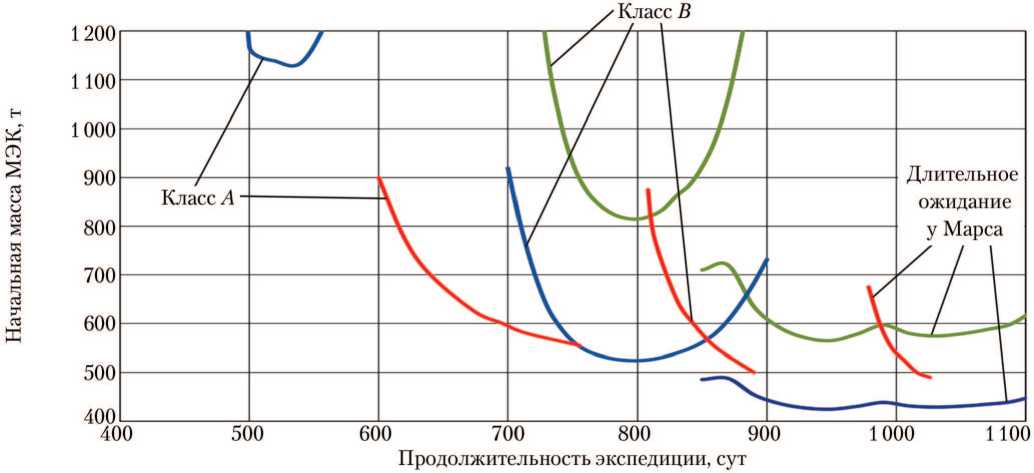
Рис. 11. Зависимость начальной массы марсианского экспедиционного комплекса (МЭК) от продолжительности экспедиции для различных вариантов энергодвигательного обеспечения при прямом входе корабля возвращения экипажа на Землю в атмосферу Земли со скоростью не более 12,5 км/с (синодический период 2049-2050 гг.): ^— — ЖРД; ^^Ш — ЯРД; ^^ш — ЯЭРДУ (рисунок создан автором)

Как видно на рис. 11, все три рассмотренных варианта ЭДК способны обеспечить близкие показатели энергобаллистической эффективности. Например, в диапазонах начальных масс МЭК 600…800 т и продолжительности экспедиции 600…800 сут возможны экспедиции с ЭДК всех трёх рассмотренных типов. С другой стороны, ни один из вариантов ЭДК не имеет решающего преимущества по одному из показателей энергобаллистической эффективности. Всё это (с учётом неопределённости принятых характеристик для каждого типа ЭДК) не позволяет выбрать предпочтительный вариант ЭДК.

На рис. 12 приведены зависимости начальной массы МЭК от продолжительности экспедиции, аналогичные приведённым на рис. 11, но построенные на неблагоприятный синодический период 2058–2059 гг. Вариант ЭДК на базе ЯЭРДУ представлен только расчётами при удельном импульсе тяги 7 000 с, но позволяет проиллюстрировать масштаб изменений показателей эффективности для неблагоприятного синодического периода. Применительно к вариантам ЭДК большой тяги на базе ЖРД и ЯРД экстремали класса А оказываются неприемлемыми вследствие огромной начальной массы МЭК (десятки тысяч тонн).

Из рис. 12 также можно сделать вывод о сопоставимости показателей эффективности различных типов ЭДК в неблагоприятные синодические периоды.

Заключение

В течение рассмотренного периода 2049–2072 гг. для каждого синодического периода обеспечиваются близкие диапазоны начальной массы МЭК (свой для каждой из рассмотренных баллистических схем экспедиции). Таким образом, возможно создание МЭК с одинаковым запасом рабочего тела вне зависимости от синодического периода старта. Продолжительность экспедиций в неблагоприятный синодический период больше продолжительности экспедиций в благоприятный синодический период не более чем на 180 сут.

Энергодвигательное обеспечение на базе двигательных установок большой тяги (ЖРД, ЯРД) не обладает возможностями возвращения экипажа на Землю с орбитальной скоростью (скорость входа КВЗ в атмосферу Земли ~8 км/с), в отличие от ЯЭРДУ. Применительно к варианту возвращения экипажа по прямой схеме (вход КВЗ в атмосферу со скоростью не более 12,5 км/с) энергодвигательное обеспечение всех вышеупомянутых типов способно реализовать экспедиции с близкими показателями энергомассовой эффективности (начальной массой

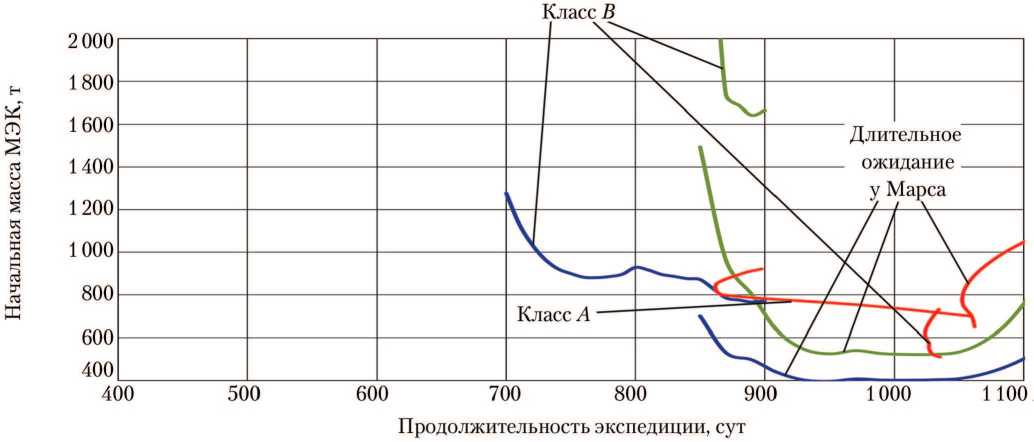
Рис. 12. Зависимость начальной массы марсианского экспедиционного комплекса (МЭК) от продолжительности экспедиции для различных вариантов энергодвигательного обеспечения при прямом входе корабля возвращения на Землю в атмосферу Земли со скоростью не более 12,5 км/с (синодический период 2058-2059 гг.): ^— — ЖРД; ^^Ш - ЯРД; ^^ш — ЯЭРДУ (рисунок создан автором)

МЭК и продолжительностью экспедиции) как в благоприятные синодические периоды системы Земля–Марс, так и в неблагоприятные.

Применительно к баллистической схеме с приближением к Солнцу (класс А ) подтверждена возможность осуществления экспедиции почти каждый год (наличие двух дат отлёта в каждый синодический период системы Земля–Марс) при практически неизменных энергозатратах на перелёт. Этот вывод остаётся справедливым как в случае возвращения с орбиты Земли, так и в случае с прямым входом КВЗ в атмосферу Земли.