Исследование энергоэффективности в ракетных двигателях малой тяги на двухфазных компонентах топлива

Энергетическая эффективность двигателей играет большую роль для любых транспортных средств, но особенно она важна для космических летательных аппаратов из-за очень жестких ограничений по массо-габаритным характеристикам.

Главным показателем энергоэффективности ракетного двигателя является удельный импульс. Важнейшей составляющей удельного импульса тяги ракетного двигателя является коэффициент расходного комплекса, показывающий полноту преобразования компонентов топлива в продукты сгорания, что обеспечивается системой подачи компонентов топлива, формирующей течение, перемешивание и взаимодействие компонентов топлива в камере сгорания. Достижение высокой полноты сгорания в ракетных двигателях малой тяги (РДМТ) осложняется характерными для таких двигателей ограниченным числом смесительных элементов (в пределе - одним) и необходимостью обеспечения допустимого температурного режима элементов конструкции за счет внутреннего охлаждения.

Появление большого числа схем организации рабочего процесса в РДМТ связано в основном с отсутствием в настоящее время надежных методов расчета процессов смесеобразования и преобразо- вания топлива в камерах сгорания. По этой причине при создании новых РДМТ требуется проведение дорогостоящей экспериментальной отработки, число натурных экземпляров при которой может составлять несколько десятков. В то же время в современных условиях жесткой конкуренции на мировом рынке космических услуг, наряду с повышенными требованиями к техническим параметрам предъявляются особые требования к минимизации сроков и затрат на создание ракетнокосмической техники.

Поэтому необходимо создание методов и методик, позволяющих еще на ранних стадиях проектирования находить конструкторские решения, обеспечивающие получение с достаточной степенью достоверности требуемых характеристик двигателей при помощи расчетно-теоретических исследований, что должно позволить исключить либо частично сократить длительный и дорогостоящий этап сравнительных испытаний.

Современное развитие вычислительной гидрогазодинамики позволяет успешно применять численное моделирование при отработке камер жидкостных ракетных двигателей, газотурбинных двигателей, газовых горелок и других энергетических установок. Примером успешного применения численного моделирования при отработке камер РДМТ на газообразных компонентах топлива являются работы [1, 2].

Преимуществом численного моделирования по сравнению с соответствующим экспериментальным исследованием является то, что численное решение задачи дает подробную и полную информацию. С его помощью можно найти значения всех имеющихся переменных во всей области решения. Кроме того, визуальное представление происходящих в камере процессов позволяет оперативно выявлять недостатки и разрабатывать пути их устранения при дальнейшем проектировании.

В продолжение работ, результаты которых приведены, например, в [2], разрабатываются математические модели и методики моделирования применительно для РДМТ на двухфазных компонентах, например О 2аз + этанол, О 2аз + нафтил. Данные топливные композиции являются экологически безопасными и рассматриваются как перспективные для РДМТ. Газификация кислорода перед подачей в РДМТ необходима для обеспечения высоких динамических характеристик.

При разработке математической модели процессов в камере РДМТ на газожидкостных компонентах топлива приняты следующие основные допущения

• 1.    Рабочее тело представляет собой сплошную неоднородную многокомпонентную газовую среду, содержащую капли распыленного жидкого горючего.

• 2.    Горение осуществляется в газовой фазе.

• 3.    Температура испаряющейся капли одинакова во всем объёме капли.

• 4.    Газовая среда включает в себя три вещества: «горючее» (в газовой фазе), «окислитель», «продукты сгорания». Все химические реакции сведены к одной необратимой брутто-реакции, описывающей стехиометрическое взаимодействие веществ «окислитель» и «горючее» с появлением вещества «продукты сгорания».

• 5.    Газовая смесь находится в локальном термодинамическом равновесии.

Комментируя данные допущения, можно отметить, что модель горения капель жидкого горючего в газообразной окислительной среде, в которой выделяются стадии прогрева капель при допущении об их объемной изотермичности, испарения и горения паров, широко применяются для подобных задач и дают удовлетворительные результаты [3–4]. Модель брутто-реакции является удобной, так как для сложной химической реакции теоретическая оценка суммарной скорости процесса затруднена вследствие недостатка точных значений кинетического механизма и констант скорости отдельных реакций. Для учета влияния на процессы реакций диссоциации и рекомбинации принята модель локального термодинамического равновесия рабочего тела, которая позволяет представлять состав как функцию состояния. В этом случае не имеет значения последовательность химических реакций при переходе к равновесию. Особенностью предложенной модели является то, что влияние на процессы реакций диссоциации и рекомбинации учтены через замыкающие зависимости от температуры и давления молекулярной массы продуктов полного сгорания, горючего, окислителя, а также их «химически равновесных» теплоемкостей. Для этого предварительно осуществляется серия термодинамических расчетов равновесного состава веществ «горючее», «окислитель», «продукты полного сгорания» при различных давлениях и температурах.

Применяя для описания процессов в камере сгорания РДМТ на двухфазных компонентах топлива дискретно-траекторный метод Эйлера– Лагранжа [5], используя и основываясь на существующий задел в области моделирования процессов в камерах сгорания тепловых машин [3–6], получим систему уравнений сохранения, соответствующую принятым допущениям:

^ + V ( r „ p v ) =_O ;

О t

О t ⁰ ( r g P v ) О t O ^ j o PEl О t

^+V ( r o p v g jV ^V J j ^- S j ;

^{+ V}' ( r a ( P V E ^- П V ⁺ q ) ) = ^V e ;

+ V ( r _a( p v ® v - П ) ) = V v ;

mi dvv. = Pi ;

^ж dt ^ж

5 1 ( m'c - ) T - Qi;

dmж л      mисп ;

dt q = -XVT + £ Jjh .

i = 1

Здесь v – вектор скорости газовой смеси, ρ – плотность газовой смеси, р – давление, ra - доля объема, занимаемая газовой фазой, gj – массовая доля j-го вещества в газовой смеси (j' ^ г, о, пс, где индекс г означает испарившееся горючее, о – окислитель, пс – продукты сгорания); П – тензор напряжений поверхностных сил [3], /иисп - мгновенный массовый секундный расход паров от i-й капли, mжi – масса i-й капли, E = cvT – внутренняя энергия газовой фазы, T – температура газовой смеси, cv – изохорная теплоемкость газовой смеси, Q, Vv, VE - источники соответственно массы, импульса, энергии, обусловленные взаимодействием газовой фазы с каплями распыленного топлива, Qi – количество теплоты, передаваемое к капле от газовой фазы в единицу времени:

Q i - Q c + Q m + Q r ,                       (9)

где составляющие Q c и Q R обусловлены соответственно конвективным и лучистым переносом; составляющая Q _m обусловлена уносом тепла от капли за счет фазового перехода

N

Q m —Z m исп r                     (10)

i-I где r – скрытая теплота фазового перехода горючего.

Диффузионный поток составляющей газовой смеси определяется как

J j =-p D j V g j ,                        (11)

где D i – эффективный коэффициент диффузии, j = г, о, пс.

Вектор результирующей силы, действующей на i -ю каплю, определяется как

P L - P d + P m + P vm + P p ,             (12)

где Р D – сила аэродинамического сопротивления, Р M – сила Магнуса, Р VM – виртуальная массовая сила, обусловленная увлечением массы газовой фазы при ускорении капли; Р р – сила вследствие градиента давления. Значения Р D , Р_M , Р_VM , Р_р определяются по зависимостям, приведенным в [6].

Источники в уравнениях (1), (3), (4) определяются следующим образом:

N

Q- Z NmИсп ;(13)

i - 1

nn

Vv - ZNiP^ + ZNm испV;(14)

i-1

n ve - z N(mиспhг - Qi),(15)

i - 1

где h _г ^п – энтальпия горючего в газовой фазе, N _i – число капель группы i в единице объема,

Источники в уравнениях типа (2):

Sг --МгvrRг + Q;(16)

Sо --М0v0Rr;(17)

Sпс - МпсVпсRг,(18)

где М г , М о , М пс , – соответственно молекулярные массы испарившегося горючего, окислителя, продуктов сгорания, v _г, v _o, v _пс - стехиометрические коэффициенты соответственно горючего, окислителя и продуктов сгорания в уравнении брутто-реакции, R _г – скорость горения, определяемая как меньшее значение из скорости перемешивания за счет турбулентных пульсаций (модель «диссипирующего вихря») и скорости химической реакции [6]:

_ e .

AB min k

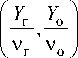
R_г - min <

e Y

B ^e Y5^ k ^v пс

K exp ( Ea /( R 0 T ) У Л Y_o^e- ) .

В последнем выражении Yг ,Yо ,Yпс – соответственно мольные концентрации горючего, окислителя и продуктов сгорания, ^г, ^о - эмпириче- ские константы, K – предэкспоненциальный множитель в законе Аррениуса, k – кинетическая энергия турбулентных пульсаций, е - скорость диссипации турбулентной энергии. Для случая горения спирта в кислородной среде [7]

( 3 Т⁷⁵ 1

К - 1,5 - 10 ¹² -см-     -; » _г - 0,15;    « _о - 1,6,

I моль I с

E - 30

ккал

моль

Приведенная система дополняется уравнениями, соответствующими принятой модели турбулентности.

Учет вторичного дробления капель осуществляется согласно [6].

Расчетная область ограничивается внутренним объемом камеры и небольшим участком расширяющейся части сопла. В качестве граничных условий для газовой фазы на входных границах задаются значения массовых расходов, температур и интенсивности турбулентной пульсации, на выходной границе – значение давления. В граничном условии «стенка» задается универсальный логарифмический профиль скоростей в приграничной ячейке. Для дискретной фазы на входной границе задается суммарный расход капель, температура, функция распределения капель по размерам.

При помощи пакета ANSYS CFX на суперкомпьютере Южно-Уральского государственного университета по представленной математической модели проведены расчеты процессов в камере действующего двигателя тягой 200 Н, работающего на композициях О 2а^з + этанол и

О2аз + нафтил. Расчеты проводились для компо зиции О2аз + этанол.

Принципиальная схема камеры двигателя (разработка НИИМаш г. Н. Салда) приведена на рис. 1.

Газообразный окислитель подается в камеру сгорания через радиальные струйные форсунки А и В и через 2 пояса завесы. Первый пояс завесы образуют радиальные отверстия В, направленные на огневое днище головки. Второй пояс завесы образуется тангенциальными отверстиями Г, расположенными на входе в дозвуковую часть сопла. Горючее через форсунки Д впрыскивается в струйные форсунки Б.

В расчетной модели форсунки Д отсутствуют, а на входе в форсунки А задается расход газообразного окислителя, содержащего капли горючего. Распределение капель по размерам задано функцией Розина-Раммлера.

На рис. 2–4 представлены результаты расчета.

Как видно из рис. 2, в пристеночной области реализуется низкая температура.

Это обусловлено тем, что кислород, увлекаемый обратными токами, создаваемыми ядром по- тока, движется в сторону огневого днища возле стенки, обеспечивая тем самым внутреннее охлаждения. Вблизи огневого днища этот кислород захватывается ядром, где участвует в горении. Линии тока, представленные на рис. 3, наглядно демонстрируют данный процесс.

На рис. 4 показаны траектории движения капель горючего.

Визуализация рабочего процесса, полученная в результате численного моделирования, дает ка-

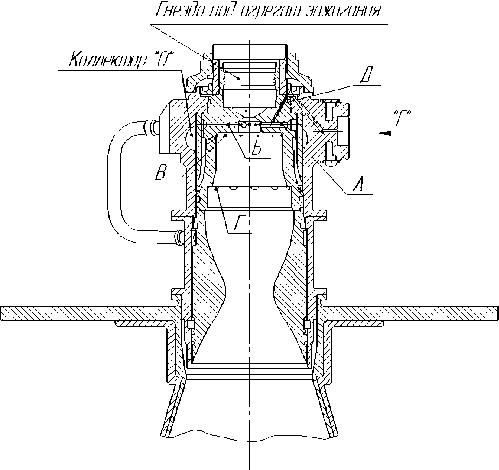
Рис. 1. Принципиальная схема камеры

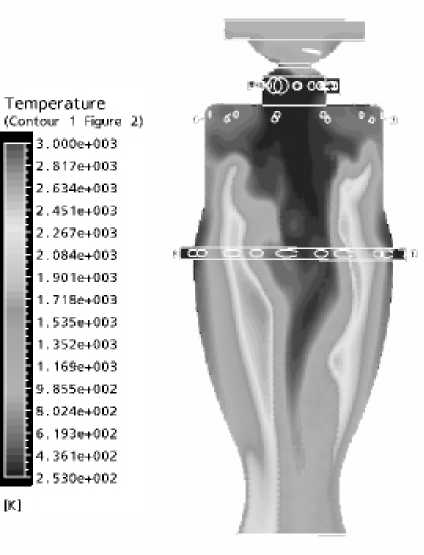
Рис. 2. Поле температур в камере

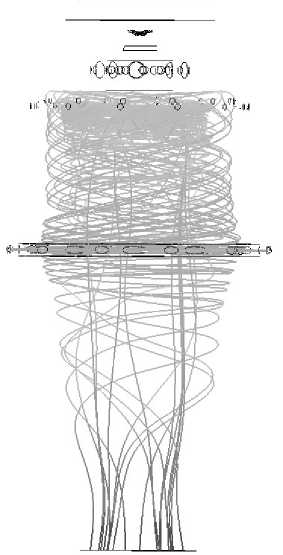
Рис. 3. Линии тока, выходящие из отверстий Г (см. рис. 1)

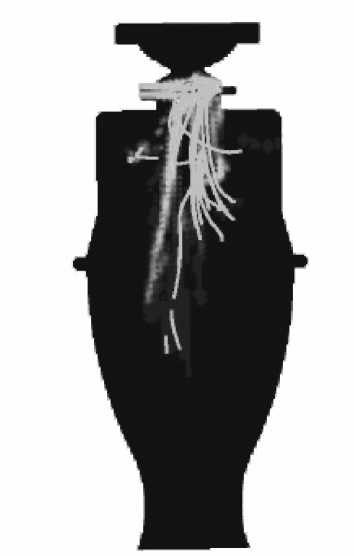
Рис. 4. Траектории капель жидкого горючего

чественное представление о протекающих процессах.

Результаты расчетов позволяют определить коэффициент расходного комплекса, который вычисляется как pF

• <'        v [8]                                 (20)

G р либо вых

• ^ф    - ^[1],               (2D

где F кр – площадь критического сечения сопла, G – суммарный массовый расход компонентов топлива, Р' - теоретическое значение расходного комплекса для конкретного топлива (окислитель, горючее, соотношение компонентов топлива), G _г ^вх – массовый расход горючего на входе в камеру, G _г ^вых – массовый расход несгоревшего горючего на выходе из камеры, р к – давление в камере сгорания, определяемое по результатам расчета.

Значения ф р , вычисленные по формулам (20) и (21) для различных расчетных моделей (различные расчетные сетки, различные модели турбулентности), составляют фр = 0,83...0,87 .