Исследование эволюционных алгоритмов для решения задачи оптимального управления

Основной подход к численному решению задачи оптимального управления состоит в редукции к задаче нелинейного программирования [1]. Следует отметить некоторые особенности данного подхода. В полученной в результате редукции задаче нелинейного программирования вычисление одного значения целевой функции требует интегрирования системы дифференциальных уравнений, что в большинстве прикладных задач занимает гораздо больше времени, чем преобразование искомого вектора на итерации в процессе поиска. Отсюда следует, что сложность алгоритма в задачах оптимального управления

«Московский физико-технический институт (государственный университет)», 2017

целесообразнее оценивать по количеству вычислений значений целевой функции, а не по количеству поисковых итераций. Заметим, что в градиентных методах на одной итерации количество вычислений целевой функции равно размерности искомого вектора, а в методах второго порядка – квадрату размерности. Часто в прикладных задачах оптимального управления вычисление одного элемента Гессиана занимает намного больше времени, чем вычисление обратной матрицы для всего Гессиана. Второй важной особенностью задачи оптимального управления является отсутствие сведений о топологических свойствах целевой функции в пространстве искомых параметров. Если целевая функция содержит большое количество локальных экстремумов, то методы нелинейного программирования будут скорее всего находить локальные экстремумы, значение которых не дает информацию о месте расположения глобального оптимума в пространстве искомых параметров. Третьей особенностью поиска численного решения задачи оптимального управления является высокая размерность пространства искомых параметров. Простейшая редукция задачи оптимального управления к задаче нелинейного программирования состоит в дискретизации компонент вектора управления по времени. При таком подходе чем больше точек дискретизации, тем точнее численное решение задачи оптимального управления, но тем больше размерность пространства искомых параметров. Достаточно сложно определить топологические свойства целевой функции, каждое значение которой вычисляется интегрированием системы дифференциальных уравнений, в пространстве большой размерности, равной произведению количества точек дискретизации и размерности вектора управления. Применение для численного решения задачи оптимального управления методов глобальной оптимизации [2] требует покрытия пространства поиска областями и их перебора для анализа. Количество областей с r точками разбиения по каждой оси в пространстве размерности p равно величине ( r + 1) ^p . Заметим, что «неподъемная» для перебора на любой вычислительной машине с любым распараллеливанием величина 2 ¹⁰⁰ соответствует одной точке разбиения на каждой оси в пространстве искомых параметров размерности 100, которая может быть получена дискретизацией по времени всего пятьюдесятью точками вектора управления из двух компонент.

В конце XX века появились эволюционные алгоритмы, которые создаются до сих пор и имеют достаточно экзотические названия [3]. С вычислительной точки зрения все эволюционные алгоритмы имеют два общих признака: они используют первоначальное множество возможных решений, которое генерируется, как правило, случайно, далее на последующих этапах выполняется изменение или эволюция этого множества за счет создания новых возможных решений на основе использования информации о ранее вычисленных значениях целевой функции для элементов множества возможных решений. При данном определении эволюционных алгоритмов все градиентные методы возможно преобразовать к эволюционным, если использовать в них начальное множество возможных решений, так как для получения нового возможного решения требуется вычисление значения градиента, которые включает вычисление значения целевой функции для текущего возможного решения.

В настоящей работе мы сравниваем наиболее популярные эволюционные и многоточечные градиентные алгоритмы на примере решения одной прикладной задачи оптимального управления, наибыстрейшего перемещения мобильного робота из одной точки плоскости в другую с учетом четырех фазовых ограничений.

2.    Задача оптимального управления

Рассмотрим задачу оптимального управления в наиболее часто используемой для численных решений постановке:

x = f(x, u), где x G Rn, x = [ xi ...  xn ]T — вектор состояния, u G Rm, u = [ u 1  ...  um ]T — вектор управления, f(x, u) = [ fi(x, u) ... fn(x, u) ]T.

Заданы ограничения на управление:

u - C u C u+, где u-, u+ — заданные постоянные векторы ограничений, u- = [ и- ... um ]T, u+ = [ u + ... um ] T.

Заданы начальные условия:

x(0) = x0, где x0 — заданный вектор начальных значений, x0 = [ x0 ... xП]T .

Заданы терминальные условия:

x( tf) = x f, где xf — заданный вектор терминального состояния, xf = [ xf ... хП]T , tf — ограниченное время процесса управления:

^{t f} ={

• t, если t < t ⁺ и | |x ( t ) — x f | | C E,

t+ — иначе, где t+ , e — заданные положительные величины, норма разности векторов может выбираться из особенностей задачи, для модели объекта с соизмеримыми компонентами вектора состояния целесообразно выбрать евклидову норму:

n

^{1 x (} t ) ^{— x} f I I =

2 ⁽ x i ⁽ t ) ^{— x f ) 2} . i =1

Заданы фазовые ограничения:

h i ( x ) C 0 , i = 1 ,..., r.

Задан функционал качества:

J = ^{1 x (} t f )

—

x ^f

I I + I" 0

(f0(x, u) + £ Xi^(hi(x))hi(x))dt i=1

^ min ,

где « i — заданные коэффициенты штрафа, i = 1 ,..., r , $ ( A ) — функция Хэвисайда:

^ ( A ) = {

1 , если A >  0 , 0 — иначе .

Результатом решения задачи оптимального управления является вектор управления с компонентами в форме функций времени u ( • ) = [ n i ( • ) ... u m ( • ) ] T , поэтому данная задача относится к классу задач бесконечномерной оптимизации. Для применения к решению задачи оптимального управления методов нелинейного программирования необходимо аппроксимировать искомые функции u i ( • ), i = 1 ,..., m , функциональными зависимостями от конечного числа параметров. Для этой цели часто используют полиномы, ортогональные ряды или кусочно-функциональную аппроксимацию.

Приведем редукцию задачи оптимального управления к задаче нелинейного программирования с помощью кусочно-линейной аппроксимации. Зададим малый интервал A t >  0

и определим количество интервалов:

M =й -

Значение управления u( t ) = [ u i ( t )

ношения

u j ( t ) = *

um (t) ] T в момент времени t определяем из соот- u-, если q(t,j,i, At) < u-, u+, если q(t,j,i, At) > u+, q(t, j, i, At) — иначе, где iAt ^ t < (i + 1)At,

q ^{( t,j,i}, ^A t ) — q ( j- 1) M + i ^{+ (} q ( j- 1) M + i +1

^^^^^^^^r

X⁽ t ^{— (} i ^{— 1)A} t ) q ( j- 1) m + i )-------A t-------,

i — 1 ,..., M,j — 1 ,... ,m .

В результате поиск управления в задаче оптимального управления заменяем поиском вектора постоянных параметров q — [ q 1 ... qp ] T, где p — m (M + 1).

При поиске значения параметров ограничиваем q- < qi < q+, i— 1 ,...,p, где q- , q+ — заданные значения ограничений на параметры, q-   ^ u-/(м+1)j+1, u+/(м+1)j +1 ^ qi+, i — 1,... ,P, LAI — целая часть числа A.

3.    Численные методы решения задач оптимального управления

Для решения задачи оптимального управления используем многоточечные градиентные методы и популярные эволюционные алгоритмы. Для градиентных и эволюционных методов первоначально генерируем множество возможных решений:

Q o — { q ^{0 , 1} ,..., q ^{0 ,H} },                                     (1)

где q0,i — [ q0,i ... qp,i ]T, qj,i — ^(qj+ -q-)+q-, i — 1 ,...,h, j — 1 ,...,p,                    (2)

величина H зависит от алгоритма и определяется по общему количеству вычислений значений целевой функции в процессе поиска, ξ — случайная равномерно распределенная в интервале от 0 до 1 величина. Среди градиентных методов используем известные методы [4]: наискорейшего градиентного спуска, метод Ньютона–Рафсона, метод Марквардта и новый метод ADAM, который был предложен в 2015 году [5] для решения задачи обучения больших искусственных нейронных сетей. Приведем описание метода ADAM. После генерации начального множества возможных решений (1), (2) задаем векторы m — [ 0 ... 0] T и v — [ 0 ... 0] T размерностью p . Задаем параметры алгоритма: малые величины е 1 и е 2 , максимальное число итераций W , константы а ~ 0 . 001, в 1 ~ 0 . 9, в 2 ~ 0 . 999, счет

∂J       ∂J ^T

∂q 1 . . . ∂q p       .

чик итераций w — 1. Вычисляем градиент целевой функции VJ (q) — Вычисляем новые значения векторов m и v по формулам mi ^ в 1 mi + (1 — в 1) д—, vi ^ в2 vi + (1 — в2) ( д— ) , ∂qi                          ∂qi i — 1,... ,p.

Формируем вектор s — [ s 1 ... sp] T по формуле si —

Am i

е 1 + Vv" i

i — 1 ,... ,p,

где A — а

1 -ew™ 1 -e w

, w E [1; W ] — номер текущей итерации. Вычисляем значение нового

вектора параметров:

q

n

— q - s .

Проверяем выполнение условий: если условие | |q — q n || <  е 2 выполнено, то достигнута заданная точность, завершаем вычисления; если условие w = W выполнено, то достигнуто максимальное число итераций и завершаем вычисления; если оба условия не выполнены, то q ^ q n ; w ^ w + 1. Среди эволюционных методов используем генетический алгоритм [6, 7], метод роя частиц [8] и пчелиный алгоритм [9, 10]. Приведем описание метода роя частиц и пчелиного алгоритма, которые не так популярны, как генетический алгоритм. В методе роя частиц на подготовительном этапе задаем размер множества возможных решений H , размер подмножества информаторов N , максимальное число итераций W . Генерируем начальное множество векторов параметров q j = [ q j ... q p ] T , j = 1 ,..., H , по формулам (1), (2). Задаем начальный вектор v j = [ v j ... v p ] T направления изменения векторов параметров:

v j = 0 , i = 1 ,... ,p, j = 1 ,... ,H.

Эволюционный процесс поиска оптимального решения продолжаем до достижения максимального числа итераций W . На каждой итерации производим вычисление вектора q ^b , доставляющего лучшее значение функционала

J (qb) = min {J (qj) : j = 1 ,...,H}, j и вычисление опорного вектора qjr, являющегося лучшим среди N случайно отобранных векторов qj1 ,...,qjN:

J (qjr) = min {J (qjk) : k = 1,... ,N}, k где ji,... ,jN — случайные целые числа в диапазоне от 1 до H. С учётом найденных лучшего qb и опорного qjr векторов строим новое значение вектора vj для каждого вектора параметров qj :

vj ^«vj + ^в(qb — qj) + ^ү(qjr — qj), i = 1 ,...,p, j = 1 ,...,h, где α,β,γ — заданные параметры, значение которых подбирают в зависимости от решаемой задачи, ^в Е [0; в] и ^ү Е [0; ү] — случайные величины. Для каждого вектора параметров qj вычисляем новый вектор qj = [ qj ... qp ] T по формуле qj

q-, если qj + Svj < q-, q+, если qj + Svj > q+, qj + Svi — иначе, i = 1,... ,p, j = 1,... ,H,

где S — заданный параметр, S ~ 1.

Если J ( q j ) > J ( q j ), то q j ^ q j , j = 1 ,...,H . Завершаем вычисления при выполнении W итераций. Решением считаем вектор с наилучшим значением целевой функции в итоговом множестве возможных решений.

Пчелиный алгоритм был предложен в 2005 году [10]. В пчелином алгоритме первоначально выявляем определенное число подобластей пространства поиска, в которых значение целевой функции меньше. Данные подобласти исследуем более интенсивно, при этом радиус отбираемых подобластей с каждой итерацией уменьшаем.

В качестве параметров алгоритма задаем размер множества возможных решений H , максимальное число итераций W , количество N элитных возможных решений, N ~ 0 . 2 H , и количество L перспективных возможных решений, L ~ 0 . 5 H , количество E новых элитных векторов, E ~ H , и количество S новых отобранных векторов, S ~ 0 . 5 H .

Задаем начальные значения векторов радиусов областей поиска r e = [ r ee ... r e ] T и r ^s = [ r S ... r ps ] T , r e >  0, r ® >  0, i = 1 ,... ,p .

Генерируем множество векторов параметров q j = [ q j ... q p ] T , j = 1 ,... ,H , по формуле (1).

Далее на каждой итерации производим вычисление значений функционала для всех возможных решений J ( q j ), j = 1 ,...,H , и производим сортировку векторов параметров по возрастанию значения целевой функции

J ( q ¹ ) ^ J ( q ² ) ^ ... ^ J ( q H ) .

Отбираем первые N элитных векторов q j , j = 1 ,..., N . Для каждого элитного вектора q j , 1 ^ j ^ N , строим набор из E векторов g ^e = [ g e ... g p ] T :

q- , если qj + ee < q- , q+, если qj + ee > q+, , i = 1, • • • ,P, e = 1, • • • ,E, qj + £e - иначе, где eie ^ [-re; re] — величина, случайно распределенная на интервале от -re до re, re — заданный вектор радиусов области поиска вокруг элитного вектора параметров, E — число новых векторов ge в области элитного вектора qj .

Если какой-либо вектор g ^e доставляет значение функционала лучше, чем вектор q ^j ,то заменяем элитный вектор q ^j :

если J ( g ^e ) < J ( q j ), то q j ^ g ^e , J ( q j ) ^ J ( g ^e ), e = 1 ,... ,E.

Векторы q j , j = N + 1 ,..., L называются отобранными .

Производим эволюцию параметров для каждого из отобранных векторов. Для каждого qj, j = N + 1,..., L, строим набор из S векторов gs = [ gp ... gp] T по формуле gis =

qi , если qj + es < qi , q+, если qj + ei > q+, , s = 1 ,...,S, qj + ei - иначе, где eS ^ [—rf; rp] — величина, случайно распределенная на интервале от -ri до ri, rs — заданный вектор радиусов области поиска вокруг отобранного вектора параметров.

Если какой-либо вектор g ^s доставляет значение функционала лучше, чем вектор q ^j ,то его помещаем во множество возможных решений вместо вектора q ^j :

если J ( g ^s ) < J ( q j ), то q j ^ g ^s , J ( q j ) ^ J ( g ^s ), s = 1 ,... ,S.

Для остальных векторов q j , j = L + 1 ,... ,H , производим генерацию новых случайных значений по формуле (1).

Далее производим уменьшение радиусов области поиска вокруг элитных и отобранных векторов:

re ^ aere, rs ^ asrs, i = 1,..., p, i ei i si где ae, as — заданные параметры уменьшения областей поиска, ae ~ 0.95, as ~ 0.95.

Процесс поиска вектора параметров продолжаем до достижения максимального числа итераций W . Лучший вектор в итоговом множестве возможных решений считаем решением задачи.

4.    Вычислительный эксперимент

Для теста методов выбрана задача оптимального управления мобильным роботом с фазовыми ограничениями.

Задана математическая модель мобильного робота [11, 12]:

іс 1 = 0.5(и 1 + u2) cos(x3), іс2 = 0.5(и 1 + u2) sin(x3), іс3 = 0.5(u 1 - u2), где x = [ x 1 x2 x3 ]T — вектор состояния, u = [ u 1 u2 ]T — вектор управления.

Заданы ограничения на управление: — 10 С u і С 10, — 10 С и 2 С 10. Заданы начальные условия: x 1 = 10, x 2 = 10, x ¹ = 0. Заданы терминальные условия: x f = 0, x f = 0, x f = 0. Заданы четыре фазовых ограничения:

hі(x) = 1.5 — V(x 1 — 2.5)2 + (x2 — 2.5)2 С h2(x) = 1.5 — V(x 1 — 7.5)2 + (x2 — 7.5)2 С hз(x) = 3 — V(xі — 2)2 + (x2 — 8)2

h4(x) = 3 — V(x 1 —8)2 + (x2 — 2)2

Задан функционал качества:

J = t f ⁺ ^/^^ ^ (M t f l -x ) ^{2 +}

+ Jtf($(hi(x))hi(x) + $(h2(x))h2(x) + $(hз(x))hз(x) + $(h4(x))h4(x))dt ^ min, где tf =

• t , если    E ³=1 ( x i ( t ) — x f ) ² С E,

t ⁺ — иначе .

Заданы параметры модели: t ⁺ = 2 . 5, E = 0 . 01, A t = 0 . 25, M = [ 4 / 0 . 25 J = 16, p = 2( M + 1) = 34, q - = — 20, q + =20, i = 1 ,...,p , X j = 1, j = 1 ,..., 4.

Необходимо найти управление в виде u k (t) = <

u- , если qi+M(k-1) + (qi+M(k-1)+1 — qi+M(k-1)) (^ — i + 1) < u- , u+, если qi+M(k-1) + (qi+M(k-1)+1 — qi+M(k-1)) (St — i + 1) > uk , qi+M(k-1) + (qi+M(k-1)+1 — qi+M(k-1)) (st — i + 1) — иначе, где iAt С t < (i + 1)At, i = 1,..., M, j = M + 1,..., 2M, k = 1, 2, q- С qi С q+, i = 1,... ,p.

Решением задачи является вектор параметров q = [ q 1 ... q _p ] T .

Для всех методов был проведен вычислительный эксперимент с общим числом вычислений целевого функционала около 130 000. Параметры алгоритмов для экспериментов имели следующие значения: в методе наискорейшего градиентного спуска количество одномерных поисков W = 60, размер множества возможных решений H = 50; в методе Ньютона-Рафсона количество итераций W = 5, H = 10; в методе метод Марквардта W = 10, H = 5; в методе ADAM 5q = 0 . 0001, e ₁ = 0 . 0001, e ₂ = 0 . 0001, a = 0 . 001, в ₁ = 0 . 9, в ₂ = 0 . 999, W = 200, H = 16; в генетическом алгоритме H = 256, вероятность мутации 0 . 7, число бит под целую часть числа 4, под дробную часть 16, число возможных скрещиваний W = 530; в методе роя частиц H = 32, a = 0 . 7278, в = 0 . 5, ү = 0 . 1, S = 1, W = 4000; в пчелином алгоритме a e = 0 . 95, a s = 0 . 95, r ^ =4, r is = 4, i = 1 ,... ,p , W = 400, H = 30, N = 6, L = 15, E = 30, S = 15.

В эксперименте также использовали случайный поиск, в котором генерировали случайно 130 000 векторов и определяли из них лучший. В каждом эксперименте выполняли по 10 запусков. Результаты эксперимента приведены в табл. 1, где использованы следующие обозначения: GA — генетический алгоритм, PSO — метод роя частиц, BA — пчелиный алгоритм, FGD — метод наискорейшего градиентного спуска, NR — метод Ньютона–Рафсона, MQ — метод Марквардта, AD — метод ADAM, RS — случайный поиск, Ср. — среднее значение, СКО — среднеквадратичное отклонение. Во всех экспериментах определяли наилучшее, среднее и среднеквадратичное значения. В каждой колонке указаны места, занятые алгоритмом по каждому показателю. В последней колонке представлена сумма мест по трем показателям.

По результатам экспериментов по всем трем показателям лучшим оказался пчелиный алгоритм. Все эволюционные алгоритмы нашли решения лучше, чем случайный поиск. Из градиентных алгоритмов многоточечные методы Марквардта и ADAM дали приемлемые результаты по значениям целевой функции.

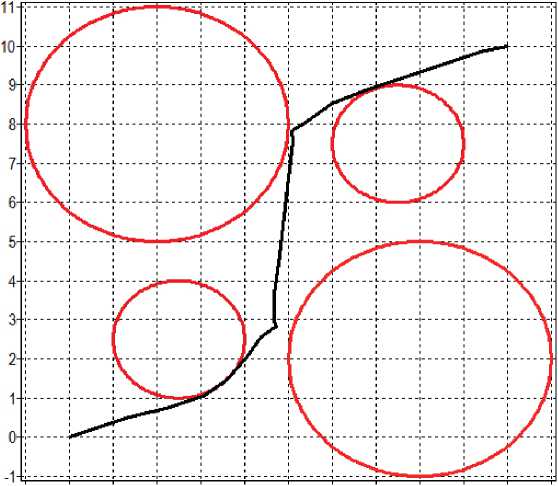
На рис. 1 представлена траектория движения робота на плоскости для лучшего найденного решения. Значение функционала для полученного возможного решения составляет 2 . 5100, число вызовов целевой функции — 132 032.

Таблица1

Сравнительный анализ результатов эксперимента

Алгоритм	Лучший результат		Среднее значение		СКО		Сумма
BA	2.5100	1	2.7306	1	0.0911	1	3
PSO	2.5302	2	2.8506	2	0.1827	3	7
ADAM	2.8185	4	3.0375	3	0.1198	2	9
GA	2.5304	3	3.0671	4	0.3988	5	12
MQ	2.8852	5	3.3991	5	0.3412	4	14
fGD	3.0267	6	3.8374	6	0.6052	7	19
RS	3.3242	7	4.4672	7	0.5515	6	20
NR	6.1135	8	8.3549	8	1.7682	8	24

1 0 1 23456789 10 11

Рис. 1. Траектория движения мобильного робота на плоскости

Найденный наилучший вектор параметров имеет следующее значение:

q =[1 . 8824 - 18 . 5686 - 2 . 7510 - 19 . 4642 18 . 1277 19 . 2901 12 . 7768 - 5 . 6104 - 15 . 9746 - 7 . 3604 - 5 . 5767 16 . 4129 4 . 4010 - 11 . 9245 - 6 . 0492 - 18 . 3288 2 . 8640

- 7 . 8236 - 11 . 8720 - 18 . 2929 15 . 5538 13 . 1515 15 . 1281 - 12 . 5568 - 6 . 5664 - 3 . 4499

- 15 . 7867 13 . 4663 4 . 2882 - 4 . 4374 - 16 . 7430 4 . 0273 - 16 . 1006 - 19 . 2252 ] ^T .

5.    Заключение

В результате анализа задачи оптимального управления, редуцированной к задаче нелинейного программирования, определены основные особенности и проблемы численного решения задачи оптимального управления методами нелинейного программирования, которые заключаются в сложности вычисления целевой функции, неопределенности топологических свойств целевой функции в пространстве искомых параметров и большой размерностью пространства поиска.

Сравнительный вычислительный эксперимент решения различными эволюционными и многоточечными градиентными алгоритмами задачи оптимального управления с фазовыми ограничениями для математической модели мобильного робота третьего порядка показал, что популярные эволюционные алгоритмы, метод роя частиц, пчелиный алгоритм и генетический алгоритм дают результаты лучше, чем многоточечные классические градиентные методы при том же количестве вычислений целевой функции. Многоточечный новый градиентный метод ADAM дает результаты, сравнимые с результатами, полученными эволюционными алгоритмами. Лучшим из всех используемых в эксперименте алгоритмов оказался пчелиный алгоритм по всем оцениваемым показателям, наилучшему найденному значению целевой функции, по среднему значению и среднеквадратичному отклонению. Все эволюционные алгоритмы показали значительно лучшие результаты, чем алгоритм случайного поиска при том же количестве вычислений значений целевой функции.

Работа выполнена при поддержке гранта РФФИ №17-08-01203-а.