Исследование качества работы алгоритмов SIFT и PHASH для задачи поиска нечетких дубликатов изображений

Поиск изображений в сети интернет является одним из самых бурно развивающихся сервисов последнего десятилетия. Потребности пользователей к данной технологии неуклонно возрастают, совершенствуется и алгоритмическая база, способная выдавать всё более полный, точный и быстрый ответ. Однако сама по себе область работы с изображениями остается еще не решенной. При всём существующем многообразии алгоритмов поиска нечётких дубликатов изображений нет точного и однозначного ответа, какой из подходов даст хорошие результаты при решении той или иной задачи.

Как правило, для поиска нечётких дубликатов изображений используются алгоритмы, учитывающие так называемые, ключевые особенности изображений или их частей, полученных после сегментации [2]. Это вполне обоснованный и логичный путь развития, так как ключевые особенности устойчивы к сдвигам, масштабированию, поворотам и другим подобным искажениям. Методы, использующие данный подход, на практике показывают довольно хорошие результаты, что обосновывает их актуальность и целесообразность дальнейшего развития. Одним из самых ярких представителей этого подхода является метод поиска SIFT-дескрипторов.

Принципиально новым, но не менее перспективным подходом в решении задач поиска нечётких дубликатов являются алгоритмы, использующие перцептивный хэш.

В отличие от вышеописанной концепции, данный подход для построения хэша использует полностью всё изображение, а не только его ключевые особенности. Для дальнейшего рассмотрения был выбран алгоритм pHash.

Прежде чем исследовать алгоритмы поиска нечётких дубликатов изображения, нужно дать определение понятию нечёткого дубликата некоторого изображения. Под нечёткими дубликатами подразумевают изображения, которые могут быть переведены друг в друга путём таких преобразований как поворот сдвиг, изменение угла обзора изменение разрешения изменение масштаба, изменение освещения [4,5]. Изображения подобного рода могут быть получены, например, при разных условиях регистрации, или при различных операциях редактирования (обрезка, масштабирование, поворот, цветокоррекция и т.д.).

Первый подход, который был рассмотрен в данном исследовании, является алгоритм, основанный на поиске ключевых особенностей изображения и построения их SIFT-дескрипторов (scale-invariant feature transform), с помощью которых осуществляется дальнейшее сравнение изображений. Алгоритм был запатентован в Канаде Дэвидом Лоу.

Данный подход является довольно эффективным в задачах поиска нечётких дубликатов изображений, так как основан на сравнении не всего изображения, а их локальных признаков. Выявленные точечные особенности изображения инварианты к масштабированию, повороту, так же частично инвариантны к изменению ракурса и освещённости. Эти особенности без труда можно выделить как в пространственной, так и в частотной областях, что позволяет снизить вероятность ошибки при искажении изображения шумами или его частичным перекрытием.

Прежде чем построить SIFT-дескриптор ключевых особенностей изображения, их предварительно нужно обнаружить на изображении. Чаще всего для определения особых точек используются пирамиды гауссианов и разностей гауссианов.

Формально гауссиан можно определить следующим образом [6]:

Gaustx.y.a) = Coretx.y.a)* Kx.yX где Gaus – значение гауссиана в точке в пикселе (x, y), а σ – радиус размытия. Core – гауссово ядро, I – исходное изображение, * – операция свертки.

Разность гауссианов получают путем вычитания гауссиана исходного изображения из гауссиана с некоторым радиусом размытия (см. рис. 1). Формально его можно определить следующим образом:

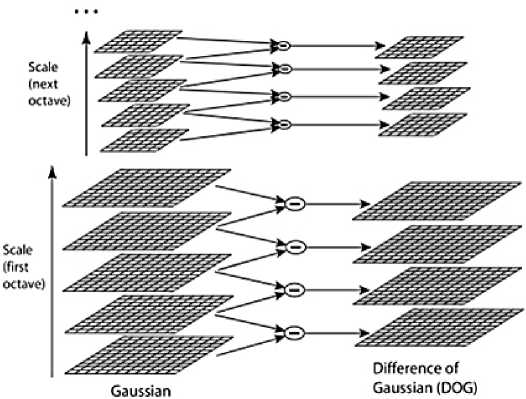
Рисунок 1. Пример разности гауссианов кальные экстремумы могут претендовать на роль ключевых. Для фильтрации используется многочлен Тейлора.

Следующим этапом является вычисление ориентации найденных точек. Направление определяется согласно градиенту точек, расположенных по соседству. При этом все вычисления градиентов выполняются на наиболее близком с точки зрения масштаба изображении. Для вычисления ориентации ключевой точки используется гистограмма направлений.

Следующим шагом является построение дескрипторов. В методе SIFT дескриптором является вектор. Как и направление ключевой точки, дескриптор вычисляется на гауссиане, ближайшем по масштабу к ключевой точке, и исходя из градиентов в некотором окне ключевой точки. Перед вычислением дескриптора это окно поворачивают на угол направления ключевой точки, чем и достигается инвариантность относительно поворота [6]. Затем на основе градиентов пикселей изображения и применению к ним свёртки с гауссовым ядром, строится непосредственно сам дескриптор. Дескриптор состоит из набора гистограмм для каждого региона свертки. Как правило, на практике (и в данном исследовании) используются дескрипторы размерностью 128 компонент.

Ещё одним подходом, для описания изображений с целью их дальнейшего сравнения между собой является концепция, основанная на использовании перцептивных хэшей. Перцептивный хэш представляет собой некую индивидуальную, но не уникальную характеристику изображения, из-за чего они могут совпадать друг с другом, в от-

Dtx.y.o)=lCoretx.y.ko)- Core(x.y.oX)»I(x.y)= Gaustx.y.ka)- Gaustx.y.a).

Если для поиска нечетких дубликатов использовать разности гауссианов, то поиск будет не чувствителен к изменению масштаба и ряду других трансформаций. Именно поэтому данный метод очень часто и используют для поиска изображений и объектов на нем.

Сам по себе гауссиан не является ключевой точкой. Для определния таких точек необходимо найти локальный экстремум из разности этих гауссианов. Однако не все ло- личие от криптографических хэш-функций таких как MD5 и SHA1. Поэтому на основе перцептивных хэшей двух изображений можно делать выводы о степени их схожести. Так как перцептивный хэш строится на основе уменьшенного изображения, то можно сказать, что идея данного алгоритма основана на работе с низкими частотами изображения.

Обобщённый алгоритм создания перцептивных хэшей можно разделить на пять следующих этапов.

• 1.    Уменьшение размера изображения. Высокие частоты изображения отвечают за мелкие детали на изображении. При уменьшении размеров мелкие детали пропадают, после чего картинка содержит информацию только о низких частотах. В большинстве случаев изображение уменьшают до размеров 8х8, чтобы общее число пикселей составляло 64.

• 2.    Перевод изображения в монохромное [3]. На этом этапе хэш уменьшается втрое и содержит только 64 значений цвета.

• 3.    Вычисление среднего значения изображения (если использовать самый простой вариант перцептивного хэша – хэш по среднему).

• 4.    Для каждого цвета вычисляется значение 0 или 1 в зависимости от того, больше или меньше оно среднего значения. На основе этого составляется цепочка битов.

• 5.    Цепочка битов, полученная на предыдущем этапе, переводится в одно 64-битное значение [1].

В отличие от представленного выше простейшего варианта – хэша по среднему, метод pHash, исследуемый в данной работе, основан на идеи доведения средних значений до крайности, применив к ним дискретное косинусное преобразование.

Так как pHash является модификацией вышеописанного алгоритма, то в данном случае его работа протекает по следующему сценарию.

• 1.    Уменьшение размера изображения. В отличие от аналогичного этапа в предыдущем алгоритме, здесь уменьшенное изображение будет иметь размерность 32x32. На этом этапе уменьшение размерности необходимо, скорее, для упрощения процесса дискретного косинусного преобразования, нежели для устранения высоких частот.

• 2.    Перевод изображения в монохромное.

• 3.    Применить дискретное косинусное преобразование, которое разложит изображение на набор частот и векторов.

• 4.    Сокращение результатов дискретного косинусного преобразования. Из всего результата работы предыдущего пункта сохраняется только верхний левый блок размерностью 8х8, так как именно он отвечает за низкие частоты в изображении.

• 5.    Вычисление среднего значения. Пункт аналогичен третьему этапу предыдущего алгоритма, но с тем отличием, что из расчёта убирается первый коэффициент.

• 6.    Присвоение каждому из 64 значений 0 или 1 в зависимости от того, оно больше или меньше среднего.

• 7.    Последним этапом является построение хэша. Для этого необходимо перевести цепочку полученных бит в 64-битное значение.

• 2.    Получение результатов работы каждого из подходов для всех сформированных коллекций (алгоритм для каждой пары изображений из коллекции возвращает долю схожести в процентах).

• 3.    Экспертная оценка схожести изображений из каждой коллекции. В качестве экспертов выступили пять человек, которым было предложено определить схожесть изображений в каждой коллекции в процентах от 0 до 100 (0 – абсолютно разные изображения, 100 – идентичные изображения).

• 4.    Далее для каждой пары сравниваемых изображений определялось насколько близка оценка обеих подходов к экспертной оценке путём их разности.

• 5.    В конечном итоге подсчитывалась сумма всех разностей для каждой пары.

  

  Рисунок 2. Примеры изображений из разных коллекций

  
  

Сравнение выбранных алгоритмов поиска нечётких дубликатов между собой выполнялись по следующему плану. 1. Подготовка исходных коллекций для тестирования методов.

Таблица 1. Пример оценок сравнения алгоритмов

	1	2	3	4	5
1	-	SIFT: 60.6569 pHash: 57.813	SIFT: 47.5086 pHash: 48.438	SIFT: 54.2114 pHash: 51.5625	SIFT: 51.2981 pHash: 43.75
2		-	SIFT: 38.3548 pHash: 53.125	SIFT: 56.625 pHash: 43.75	SIFT: 34.6231 pHash: 60.9375
3			-	SIFT: 51.7369 pHash: 56.25	SIFT: 54.4304 pHash: 48.4375
4				-	SIFT: 47.8309 pHash: 45.3125

Таблица 2. Оценки экспертов для первой коллекции

	1	2	3	4	5
1	-	(20+30+65+40+10)/5 = 33	(70+70+75+70+60)/5 = 69	(85+80+55+70+85)/5 = 75	(40+10+20+10+10)/5 = 18
2		-	(25+20+45+30+25)/5 = 29	(15+30+57+40+20)/5 = 32,4	(10+10+30+20+10)/5 = 32
3			-	(70+80+60+60+80)/5 = 70	(65+90+30+90+20)/5 = 59
4				-	(20+40+30+20+5)/5 = 23

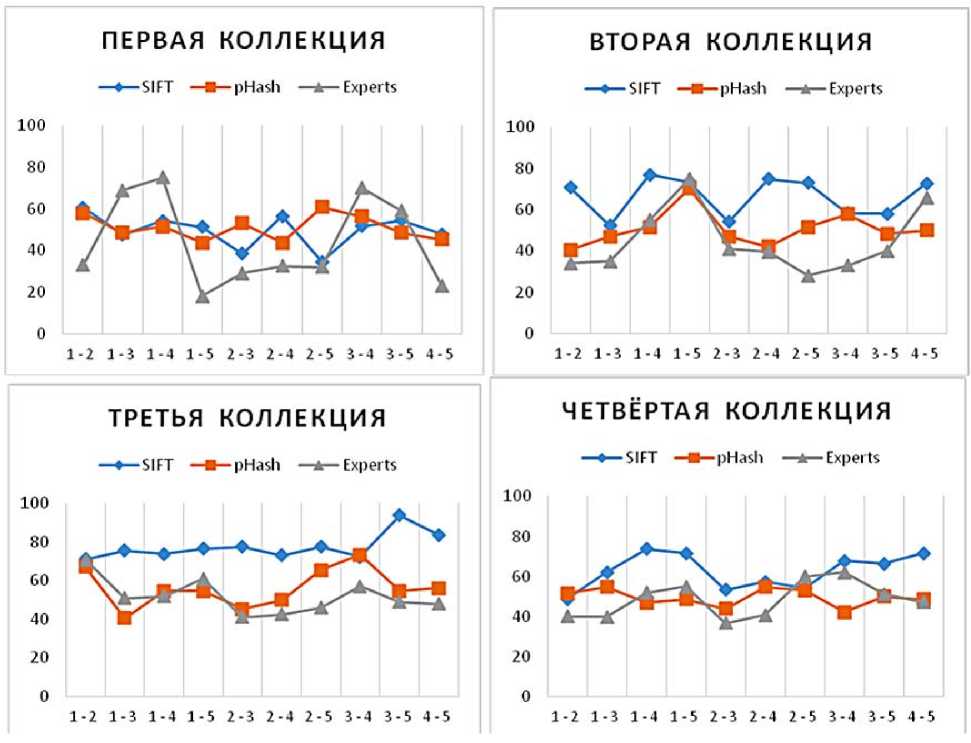
Рисунок 3. Сравнение результатов для изображений из разных коллекций

В данном исследовании под коллекцией изображений понимается набор картинок, на которых присутствует один и тот же объект, но изображён он в разных условиях (например, изменён ракурс, освещение, частично перекрыт другими объектами и т.д.). Таким образом, каждая коллекция представляет собой набор нечётких дубликатов, имеющих разную степень схожести друг с другом.

При первом подходе степень схожести двух изображений определяется путём вычисления Евклидова расстояния между SIFT-дескрипторами изображения. Во втором подходе, при сравнении двух перцептивных хэшей используется расстояние Хэмминга, так как данные хэши представляют собой последовательность бит. Точным будет считаться тот алгоритм, результаты которого будут наиболее близки к усреднённой экспертной оценке. Для этого вычисляется сумма разностей между экспертной оценкой и оценкой степени схожести алгоритма. Помимо непосредственных результатов работы алгоритмов учитывается так же скорость их работы и простота реализации.

Для проведения экспериментов над алгоритмами SIFT и pHash для поиска нечётких дубликатов были сформированы четыре коллекции. В каждой из коллекции присутствует ключевой объект, который был сфотографирован при различных условиях, таких как изменение ракурса, из- менение освещения и т.п. Примеры изображений из двух разных коллекций показаны на рис. 2.

Ниже, таблице 1, представлен пример оценок, полученных при сравнении изображений здания университета, показанных на рис. 2.

Для того, чтобы проверить, насколько точны алгоритмы, изображения коллекций были предоставлены для сравнения пяти экспертам. Это было сделано для того, чтобы рассчитать разность между оценкой алгоритмов и оценкой экспертов. После этого по каждой паре изображений производился подсчёт разности. Далее все полученные разности были просуммированы. В таблице 2 приведена усреднённая оценка схожести фотографий экспертами для той же самой серии изображений.

Чтобы наиболее полно представлять уровень схожести результатов алгоритма с результатами, полученными в процессе экспертной оценки, были составлены диаграммы для каждой коллекции. Фрагменты этих диаграмм представлены на рис. 3.

Более детальный результат сравнения и средняя разность (несогласованность с мнением экспертов) представлены в таблице 3. При этом в таблице показаны данные только для 5 пар изображений из каждой коллекции.

Для первой коллекции средняя разница между результатами алгоритма SIFT и оценкой экспертов составила

Таблица 3 . Определение степени схожести результатов работы алгоритмов с экспертной оценкой для разных коллекций

	SIFT	pHash	Expert	Δ SIFT	Δ pHash
Коллекция 1
1-2	60.65	57.81	33	27.65	24.81
1-3	47.50	48.43	69	21.49	20.56
1-4	54.21	51.56	75	20.78	23.43
1-5	51.29	43.75	18	33.29	25.75
2-3	38.35	53.12	29	9.35	24.12
2-4	56.62	43.75	32.4	24.22	11.35
2-5	34.62	60.93	32	2.62	28.93
3-4	51.73	56.25	70	18.26	13.75
3-5	54.43	48.43	59	4.56	10.56
4-5	47.83	45.31	23	24.83	22.31
Средняя разность (D1)				18.7	20.5
Коллекция 3
1-2	71.23	67.18	71	0.23	3.81
1-3	75.73	40.62	51	24.73	10.37
1-4	73.92	54.68	52	21.92	2.68
1-5	76.69	54.68	61	15.69	6.31
2-3	77.59	45.31	41	36.59	4.31
2-4	73.29	50	42.6	30.69	7.4
2-5	77.67	65.62	46	31.67	19.62
3-4	72.52	73.43	57	15.52	16.43
3-5	93.92	54.68	49	44.92	5.68
4-5	83.84	56.25	48	35.84	8.25
Средняя разность (D3)				25.78	8.49

	SIFT	pHash	Expert	Δ SIFT	Δ pHash
Коллекция 2
1-2	70.74	40.62	34	36.74	6.62
1-3	52.22	46.87	35	17.22	11.87
1-4	76.88	51.56	55	21.88	3.43
1-5	73.45	70.31	75	1.54	4.68
2-3	54.14	46.87	41	13.14	5.87
2-4	75.02	42.18	39.6	35.42	2.58
2-5	73.10	51.56	28	45.10	23.56
3-4	58.32	57.81	33	25.32	24.81
3-5	58.01	48.43	40	18.01	8.43
4-5	72.79	50	66	6.79	16
Средняя разность (D2)				22.12	10.79
Коллекция 4
1-2	48.79	51.56	40	8.791	11.56
1-3	62.15	54.68	39.6	22.55	15.08
1-4	73.75	46.87	51.8	21.95	4.92
1-5	71.64	48.43	55	16.64	6.56
2-3	53.33	43.75	36.6	16.73	7.15
2-4	57.26	54.68	40.6	16.66	14.08
2-5	53.96	53.12	60	6.03	6.87
3-4	67.66	42.18	62	5.66	19.81
3-5	66.27	50	51	15.27	1
4-5	71.53	48.43	47	24.53	1.43
Средняя разность (D4)				15.48	8.85

D1(SIFT)=18.71. Для этой же коллекции разница между результатами алгоритма pHash и оценкой экспертов составила D1(pHash)=20.56. При этом данная коллекция состояла из фотографий строений, в которых достаточно много мелких объектов и переходов (стены, окна и т.д.). На подобных изображениях алгоритм SIFT дал лучше результаты по сравнению с pHash, хотя разница между ними не столь значительна.

Для второй коллекции разница между результатами алгоритма SIFT и оценкой экспертов составила D2(SIFT)=22.12. Для этой же коллекции разница между результатами алгоритма pHash и оценкой экспертов составила D2(pHash)=10.79. В этой коллекции алгоритм на основе хеширования показал себя гораздо лучше. Дополнительный анализ показал, что это связано с наличием хорошо выделяющегося контрастного объекта на практически отсутствующем фоне.

Этот эффект сохранился и на третьей коллекции, в кторой центральный объект так же занимал значительное пространство. Для этой коллекции разница между результатами алгоритма SIFT и оценкой экспертов составила D3(SIFT)=25.78. Для этой же коллекции разница между результатами алгоритма pHash и оценкой экспертов составила D3(pHash)=8.49.

Четвертую коллекцию представляли изображения, практически полностью представляющие некоторый объект. Фона и второстепенных объектов на таких изображе- ниях практически не было. Для этой коллекции разница между результатами алгоритма SIFT и оценкой экспертов составила D4(SIFT)=25.78. Для этой же коллекции разница между результатами алгоритма pHash и оценкой экспертов составила D4(pHash)=8.49.

Как видно из представленных выше таблиц и рисунков, в трёх из четырёх коллекций ближе к мнению экспертов оказались результаты работы алгоритма pHash. Стоит так же отметить, что и скорость работы алгоритма pHash была выше, чем у алгоритма SIFT.

На первой коллекции изображений меньшую погрешность дал алгоритм SIFT. Однако в остальных случаях довольно маленькую погрешность дал алгоритм pHash. Стоит отметить, что для первой коллекции изображений погрешности алгоритмов не сильно отличаются. При этом, чем более существенную роль выполняет на изображении некоторый центральный объект, тем более качественным является работа алгоритма pHash. Если же изображения не содержат такого объекта или содержится множество мелких элементов, то алгоритм на основе ключевых точек справляется с задачей лучше.

Так же в процессе работы с двумя алгоритмами было замечено, что алгоритм pHash работает быстрее, чем SIFT. Возможно, это связано с тем, что и сами дескрипторы второго алгоритма имеют меньшую длину, чем дескрипторы алгоритма SIFT. Из преимуществ алгоритма pHash стоит так же отметить и простоту его реализации.