Исследование каспоидной фокусировки A3 методом локальной асимптотики

ВЕСТНИК 2016

В настоящей работе в соответствии с волновой теорией катастроф [1–4] исследована фокусировка, образованная параболическим волновым фронтом методом локальной асимптотики, и выполнено математическое моделирование амплитудной и фазовой структур волнового поля в окрестности особенности.1234

На рис. 1 представлена лучевая структура (тонкие линии), их огибающая – каустика (толстая линия) и волновой параболический фронт (штриховая линия), описываемый формулой (1) с a = 2. Волна падает сверху вниз вдоль лучевых траекторий, перпендикулярных к волновому фронту из затенённой области:

f ( e ) = - - ae . (1)

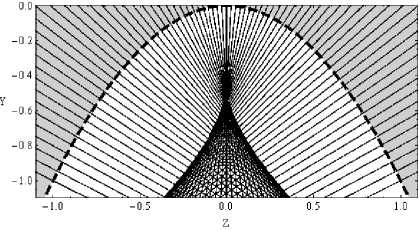
Рис. 1. Лучевая структура, каустика и волновой фронт

В формуле (1) координата ξ волнового фронта соответствует Z , а координата f ( f ) - координате Y .

Расстояние между точкой волнового фронта и точкой наблюдения ( Z , Y ) определяется формулой:

r = 7 ( y - f e ))² + ( z - e )². (2)

В соответствии с принципом Ферма (принципом наименьшего действия), уравнение лучевой траектории определяется нулем первой производной функции (2) по ξ :

dR = (fe) - y ) fxe)+e - z=0         (3)

de             R               •

Для того чтобы найти положение каустики, необходимо дополнить уравнение (3) нулем второй производной функции (2) по ^ . С учетом выполнения уравнения (3), получаем:

( f ' ( 5 )) 2 + ( f ( 5 ) — Y ) f " ( 5 ) + 1 = 0.          (4)

Учитывая (1), находим, что уравнение каустики в параметрической форме имеет вид:

Y = - - - 3 a 5 * a 2

Z = - a 5

или в неявной форме:

Z ² =-—

1 Y

a

что очевидно полукубическая парабола. Точка, в которой сливаются ветви каустик, называется каустическим остриём и соответствует каспо-идной катастрофе A₃ , в то время как сами ветви каустики – катастрофе A₂ . Каустическое остриё в данной задаче образуется в точке с координатами ( Z_с = 0, Y_с = –1 /a ), а в случае a = 2 – в точке с координатами ( Z_с = 0, Y_с = –1 / 2), что соответствует рис. 1.

Волновое поле в скалярном приближении Кирхгофа имеет вид:

U(Z, Y) = e7=- 4k Г A(5) J1 + (f (5)) exp(ikR)d5, (7) V 2п   _J„           R где k = to / c = 2п / X - волновое число, го - частота, с = 3∙108 м/c – скорость света, λ – длина волны. Далее будем считать, что A = 1, а величины (Z, Y) - координаты точки наблюдения.

Интересно отметить, что если бы фокусировка была идеальной, то есть все лучи сходились бы в одну точку, то в этой точке интенсивность поля была бы бесконечно большой (в случае бесконечного волнового фронта), что явно не имело бы физического смысла. Однако для каспо-идных фокусировок (и вообще для катастроф с конечной определенностью) это не так. Причем, края волнового фронта при достаточно большом удалении от центрального фокуса вообще мало влияют для значения поля в нём.

Проблема построения асимптотических решений является сложной задачей [5]. Согласно волновой теории катастроф (см., например, [1; 6]), в окрестности каустического острия поле представимо в виде функции Пирси и её производных:

Гм/. г⁹ I( X , X )     ⁹ 1( X , X ) 1

Up, = ^exp[ i ^у] l i^{( X} i, х) + l ₂ —а2- + l з — 4-^- ,W

L                  дХ1           дХ2 J где I(X,X2) = Jexp[i(s4 + X2s2 + Xs)]ds        (9)

-to

– функция Пирси [7]. Для того чтобы перейти от интеграла (7) к разложению (8), воспользуемся методом локальной асимптотики (ЛА) [6; 8; 9]. Локальная связь аргументов функции Пирси λ ₁, λ ₂ и фазы бегущей волны θ с пространственными координатами Z , Y имеет вид:

X « Y1 z (Z - Zc) + Yiy(Y - Yc),(10)

X2 « у2z (Z - Zc) + Y2y (Y - Yc),(11)

⁸ « - +⁶4 ( ^Z - ^Z c )+^S4 ( ^Y - Y c ) +

+ ^{1 д} - ( y - Y ) 2 + ³ - ( z - Z_c ) 2 | +

2(ay2V c’ дz2V

+-д-- (Y - Y )(Z - Z ) + AxA X dydzv    cA c)p

X dA- (Y - Y )l d A (Z - Zc )|,(12)

(d5dYv     c’ d5dZvc где [10] - = kR ,

Ap = Py (Y - Yc) + pz (Z - Zc),(13)

P h =

д - | д - , 7 д - T , d - T | + 3 T + T , (d54 J (д53дh   д^дh 2 д5дh 3 J h = Z, Y.

В формулах (10–14) координаты ( Z_c , Y_c ) – это пространственные координаты геометрического центра каустического острия. Все производные вычислены в этой точке. Выражения для коэффициентов Y i j были получены в работе [6] (см. также [8; 9; 11; 12]). Они имеют вид:

ВЕСТНИК 2016

Л д 2 -             _к д² -

Y 1 z = ^Vk^A^TUU , Y 1 y = ^Vk^A^TTU , д 5 д Z           д5 д Y

V

Y 2 z = "]T ^A

V _k Л2

^{Y 2 Y} = 2 ^A

A

д - T ₊ д - J д 5 д Z ² д²5 д Z ^j , д ² - _т , д ³ - ¹

T                       , д5 дY 2 д25 дY J

где в случае каустического острия

T ₃

Г 2	4 |	1/4 , Т 2 = - 551 55	1 - ^555
( -. 1	5) 5 1J ( 21		10 - 545 5 2     /л(6)     ^ - 555555
20	20 (	^ - 545 5 j	- 55) 5 j

,

,

^V k = sign ( - 55.55 ) .

На рис. 2–7 коэффициенты подобия

(18) (аргу-

менты функции Пирси) λ ₁, λ и фаза бегущей

ВЕСТНИК 2016

волны θ , вычисленные методом локальной асимптотики, сопоставлены с результатами, полученными методом глобальной асимптотики (ГА) [13; 14], то есть методом седловых точек. Выражения для λ ₁, λ ₂ и фазы θ (см., например, [6]) имеют вид:

- 22 = 4 2 ^{1/2 1} Sign П (1 - ф )^1/2 +

+

w

- =±V2I ^- - ^{144 2}

54 - 2

,

где

^

2 = -

1/2

I , e = ~ ~+ kR s ,

1   / О О     ОО     0   0

—k ² 1 R (1) R (2) + R (2) R (3) + R (3) R (1)

ООО

П = k ³ R (1) R (2) R (3) ,

( i , -

Ф = | 1 — П ² 2

(    4

^R s = ^ ^R ( j ) .

³ j = 1

1/3

| , R _G) = R _G) - R s ,

Значения R _{( j )} – это значения функции (2) в седловых точках, то есть при тех значениях ξ , которые являются решениями уравнения (3). Внутри каустического острия таких действительных решений три, и именно эту область мы будем рассматривать ниже при сопоставлении с локальной асимптотикой.

На рис. 2 и 3 показаны линии равного уровня фазы бегущей волны θ .

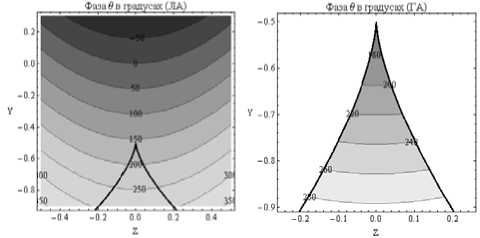
Рис. 2

Линии равного уровня фазы бегущей волны, метод ЛА – рис. 2, метод ГА – рис. 3

Рис. 3

Видно, что линии уровня имеют кривизну, центр которой находится в верхней части рисунка. На небольших расстояниях от центральной точки линии почти прямые (см. рис. 3). Поскольку при построении локальных выражений для фазы использовались квадратичные поправки, совпадение результатов, полученных методами локальной и глобальной асимптотики, очень хорошее.

На рис. 4 и 5 показаны линии равного уровня аргумента λ ₁. На рис. 4 линии уровня параллельны вертикальной оси. При вычислении аргумента использовалось только первое, линейное, приближение. Поэтому небольшая кривизна линий равного уровня, заметная на рис. 5 (нижняя часть), отсутствует на рис. 4.

На рис. 6 и 7 показаны линии равного уровня аргумента λ ₂. На рис. 6 линии уровня параллельны горизонтальной оси. Сопоставляя рис. 6 и рис. 7, видим, что кривизна линий уровня на рис. 7 заметна, что наводит на мысль о необходимости учета второго приближения. Отметим, что при увеличении параметра k (волнового числа) всё большее число осцилляций втягивается в область, хорошо описываемую первым приближением.

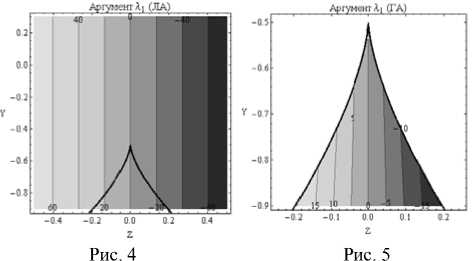
Линии равного уровня аргумента λ ₁ , метод ЛА – рис. 4, метод ГА – рис. 5

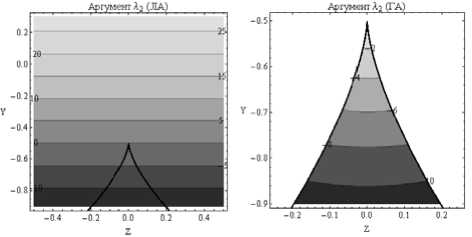
Рис. 6

Линии равного уровня аргумента λ ₂ , метод ЛА – рис. 6, метод ГА – рис. 7

Рис. 7

Локальные выражения для коэффициентов

асимптотических разложений имеют вид:

l_x ~A B   , l₂ «- i A ² v — + B ^x T ,

1           ^=0 ’ 2               k

Vd^)

l «- 1 A ³ v ^ld B + 3 ^-BT, + B X T )   , (23)

3k23

2 l5£     5 £)

где

B = ke exp [ - i n 1 4 ] J ^{1 +} ( ^f(l )) .        (24)

Для расчета функции Пирси и ее производных использован метод поворота контура интегрирования [15]. Для этого функция Пирси и ее производные представлялись в виде:

I(X,X2) = J exp[i(s4 + Xs2 + Xs)]ds +

+ J exp [ i ( s ⁴ + X ₂s ² - X s ) ] ds ,             (25)

ai(x,X) 7

• —dx—~ = j is exp [_ i (s + X2 s + X s)] ds -

• - f is exp [ i ( s ⁴ + X s ² - X 1 s ) ] ds ,             (26)

a i ( X , X ) d X ₂

+^

= J is2 exp ^ i (s4 + X s2 + X s)] ds +

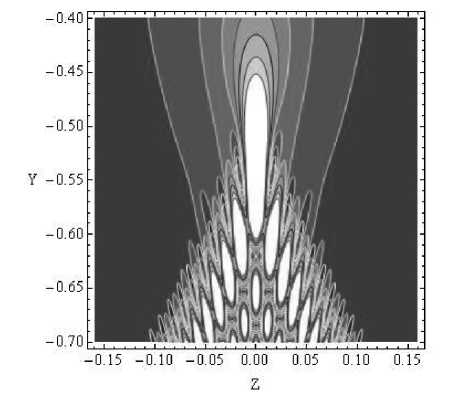
Рис. 9. Линии равного уровня амплитуды волнового поля (фрагмент рис. 8)

+⁺ J is ² exp [ i ( s ⁴ + X 2 s ² - X s ) ] ds ,           (27)

и внутренняя переменная интеграла s заменялась выражением s exp [ i n /18 ] для линий равного уровня и на s exp [ i n / 38 ] - для 3D-U3o6pa-жения. Уменьшение угла поворота контура интегрирования, увеличивая точность, расширяет диапазон параметров, при которых интегралы сходятся, но увеличивает время вычислений.

Результаты вычислений представлены на рис. 8–11 (длина волны λ = 0,02). На рис. 8–10 показана амплитуда, а на рис. 11 – фаза.

Амплитудная структура характеризуется центральным фокальным пятном, соответствующим точке слияния ветвей каустики, и мелкой

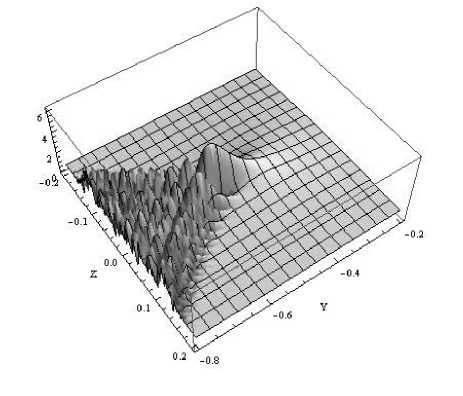
Рис. 10. 3D-изображение амплитуды волнового поля

ВЕСТНИК 2016

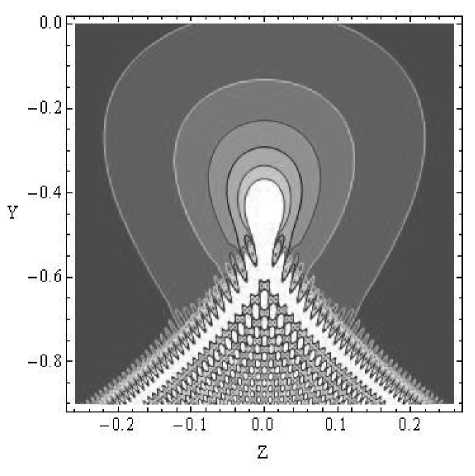
Рис. 8. Линии равного уровня амплитуды волнового поля

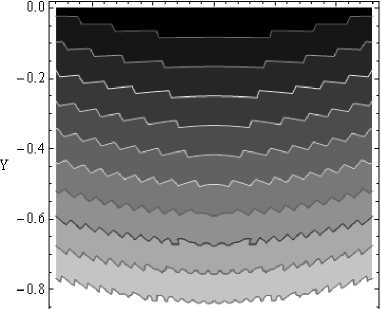
0.2 ' ' -O.i ' ' О О ' ' 0.1' ' ' О.'з Z

Рис. 11. Линии равного уровня фазы волнового поля

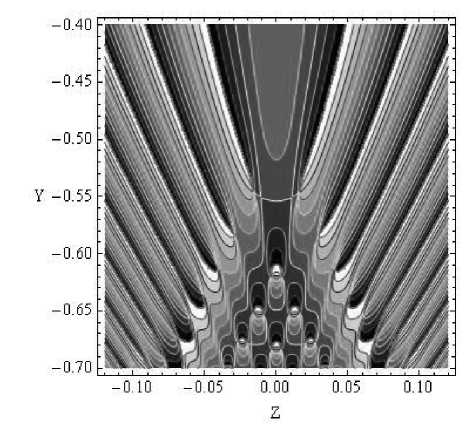
Рис. 12. Линии равного уровня фазы волнового поля без учета фазы бегущей волны

ВЕСТНИК 2016

интерференционной структурой внутри ветвей. Линии максимумов и минимумов повторяют направления ветвей каустик. Линии равного уровня фазы волнового фронта (рис. 11) являются суммой фазы бегущей волны (рис. 2 и 3) и фазы функции Пирси и ее производных (рис. 12), что приводит к характерной ряби на линиях равных уровней.

Таким образом, в работе исследованы методы построения асимптотических решений в области фокусировки каспоидного типа. Сопоставлены методы получения коэффициентов подобия: метод локальной асимптотики и метод глобальной асимптотики и построены амплитудная и фазовая структуры. Такие особенности возникают в различных оптических и радиофизических задачах, например при математическом моделировании распространения радиоволн в анизотропной неоднородной ионосфере Земли [16–17].