Исследование кинематических характеристик цилиндрических прямозубых передач, формообразуемых накатыванием средствами САПР

Широкий спектр применения передаточных механизмов на основе зубчатых колес порождает разнообразие требований к их свойствам, что влечет за собой разнообразие применяемого инструментально-технологического обеспечения их качества, выбор которого должен в максимальной степени удовлетворять конкретному набору требований к передаче. Можно отметить, что общим требованием для всех типов передач является обеспечение работоспособности с заданной вероятностью безотказной работы. Однако и здесь различия в реальных условиях работы и расчетный ресурс, от единиц минут до десятков лет, требуют выбора конкретной совокупности средств реализации, начиная с определения адекватных техническому заданию на проектирование геомет-рически-кинематических параметров передачи. Этот подход обусловлен тем, что геометрия профилей контактирующих пар определяетхарактер взаимодействия зубьев при передаче нагрузки и, следовательно, интенсивность их изнашивания, а в конечном счете и ресурс работы.

В многоступенчатых приводах космических аппаратов, в частности механизмах поворота антенн, наиболее важную роль играетпервая ступень привода. Так, например, анализ статистики отказов привода в работе [1], показывает, что наибольшему износу подвержены первая и третья ступень. Установлено [1; 2], что кинематическая неточность первой ступени вызывает динамическую нагрузку на вторую и дальнейшие ступени. На третьей ступени крутящий момент достигает достаточной величины и колебания окружной скорости ведущего колеса, в частности в момент пуска, приводят к возникновению ударной нагрузки. Одним из способов решения данной проблемы является минимизация колебаний угловых скоростей в зубчатых парах привода. Этого можно достигнуть путем оптимизации параметров зубчатой пары и высокой точности изготовления.

В механизмах поворота антенны наиболее критичным параметром являются колебания шага зубьев, которые в первую очередь приводятк возникновению колебаний в угловых скоростях ступеней привода. Второй момент – обеспечение плавного входа в зацепление путем выбора таких параметров пары, при которых угол между касательными к профилям сопряженных зубьев, проходящими через точку контакта в момент входа зубьев в зацепление, будет близким к нулю (либо минимально возможным). Одним из эффективных способов решения данной проблемы является использование накатных зубчатых колес [2].

Существующие технологии изготовления накатных зубчатых колес позволяют получить передачи, обладающие рядом преимуществ по сравнению с полученными резанием, но имеющие более низкую кинематическую точность. Современные средства компьютерного моделирования позволяют на этапе проектирования с достаточной степенью достоверности оценить качество синтезируемой передачи и обеспечить необходимый и достаточный уровень качественных показателей.

В работе [3] разработана методика имитационного моделирования процесса формообразования мелкомодульных зубчатых колес в пакете MSC.Marc 2007. В результате моделирования была получена геометрия накатного колеса. В данной работе представлено сравнительное исследование кинематических характеристик «накатанных» и «нарезных» передач. Исследование кинематических характеристик зубчатой пары проводилось в САЕ-пакете MSC.visualNastran Desktop 2005. Данный САЕ-пакет позволяет моделировать кинематику, динамику и напряженно-деформированное состояние механизмов и узлов деталей машин [4]. Для сравнения кинематических характеристик использовался привод с накатным (полученным по авторской методике) и нарезным (полученным по стандартной методике) зубчатым колесом.

Необходимо отметить, что при численном моделировании кинематики зубчатого привода принимаются следующие допущения: отсутствует погрешность шага зубчатого колеса, полученного резанием, отсутствуют деформации профилей колес под нагрузкой, не учитываются технологические зазоры, не учитывается пятно контакта, материал изотропен. В модели нетпогрешности шага вследствие огрехов изготовления, обусловленных спецификой построения моделей зубчатых колес в CAD-пакетах. В связи с вышеизложенным зубчатая пара с нарезным зубчатым колесом, спроектированным по стандартной методике, выбрана в качестве эталона для сравнения.

В процессе исследования кинематики привода были проанализированы несколько пар с итеративно изменяемыми параметрами геометрии как профиля накатываемого колеса путем смещения накатника в процессе формообразования, так и накатника. В качестве начальных параметров для моделирования была взята зубчатая пара со следующими параметрами: m =0,3 мм, z ₁ = 198, z ₂ =76, x ₁ и x ₂ =0.

Все варианты моделировались с одинаковыми граничными условиями. В качестве граничных условий на шестерне задано вращение со скоростью 6 000 град/с

(1 000 об/мин). На колесе задан моментсопротивления 1 Н·м и демпфирование 0,001 Н·м. Перемещения шестер-нииколесаво всех направлениях запрещены (рис. 1).

В качестве параметров решателя заданы:

– точность позиционирования – 1 · 10–5 м;

– точность вращения – 1 · 10–4 град;

– точность сборки – 1 · 10–6 м;

– точность связывания – 1 · 10–4 м;

– количество значимых цифр–6;

– время интегрирования – 5 · 10–6 с.

Рис. 1. Модель для исследования кинематики зубчатой пары в MSC.VisualNastran

Параметры материала колес:

– плотность – 7 850 кг/м3;

– модуль упругости – 2.1 · 1011 Па;

– коэффициентПуассона – 0,29;

– коэффициентреституции – 0,7;

– коэффициенттрения – 0,15.

Транслирование геометрии колеса, полученного накатыванием, из MSC.Marc в MSC.VisualNastran напрямую из-за специфики пакетов не представляется возможным. Для этого координаты узлов деформированной конечноэлементной сетки передаются в CAD-пакет Solidworks. Далее при помощи сплайнов происходитвосстановле-ние геометрии колеса. В данном случае неизбежно воз-никаютпогрешности при аппроксимации. Также погрешность возникает в процессе моделирования формообразования накатыванием (из-за постоянного перестроения конечно-элементной сетки происходит «сглаживание» острых кромок) (рис. 2). При визуальном сравнении нарезного (рис. 2, а ) и накатного (рис. 2, б ) колеса видны различия в геометрии. Отличается впадина и вершина зуба – накатной зуб более прямой и имеет сужение вершины. Это сказывается на характере передачи движения и величине бокового зазора.

В качестве основного результата моделирования получаем график изменения угловой скорости колеса (град/с) за время (с) (рис. 3). Так как угловая скорость шестерни – величина постоянная, то разделив угловую скорость колеса на угловую скорость шестерни, получаем график изменения передаточного отношения, идентичный изменению угловой скорости колеса.

В проведенных численных экспериментах моделировалось взаимодействие накатного колеса шестернями, нарезанными с различными коэффициентами смещения. Экспериментальным путем было установлено, что переходные процессы, возникающие в начальный момент движения, заканчиваются за 0,005 с. Все приведенные результаты сравнивались на временном отрезке 0,01 с. За это время в зацепление входят 5 пар зубьев.

а

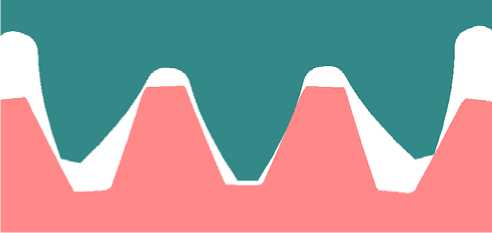
б

Рис. 2. Сравнение геометрии пар с нарезным ( а ) и накатным ( б ) зубчатым колесом

В результате было промоделировано 10 вариантов с различными параметрами (табл. 1). После каждой итерации производилась оценка результатов и определялись параметры следующего решения.

На графике изменения угловой скорости колеса видны значительные колебания (см. рис. 3). Среднее значение угловой скорости составляет 1 699,47 град/с. Среднее арифметическое отклонение (величина, показывающая среднюю величину отклонения угловой скорости отее среднеарифметического значения за анализируе-

Таблица 1

Параметры колес

Параметры	Варианты
	1*	2	3	4	5	6	7	8	9	10
Коэффициентсмещения накатника	–	0	0	0	0	0,1	–0,1	–1	–2	–0,5
Коэффициентсмещения колеса	0	0	0	0	0	0	0	0	0	0
Коэффициентсмещения шестерни	0,3	0,3	0,5	0,7	0,95	0,95	0,95	0,95	0,95	0,95

* – эталонное нарезное колесо мый период времени) для данной передачи составляет 58,07 град/с.

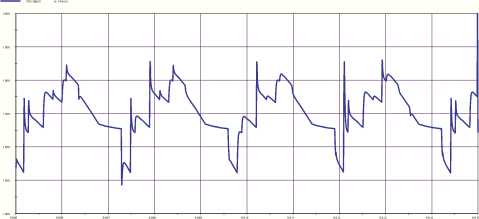
Рис. 3. График изменения угловой скорости колеса ( x ₁ = 0,3)

График сравнения результатов моделирования кинематики зубчатых пар с накатными колесами представлен на рис. 4.

Использование оригинальной методики проектирования накатных зубчатых передач [5] приводов космических аппаратов позволяет оптимизировать геометрию колеса по заданным параметрам. В процессе перебора вариантов (табл. 2) можно наблюдать степень влияния таких параметров, как коэффициенты смещения на накат- нике, коэффициенты смещения на колесе, межосевое расстояние, на колебания угловой скорости.

Предложенная методика предполагает итеративное приближение к заданным показателям качества. Проведенные исследования показали возможность управлять качественными показателями накатных зубчатых колес на этапе проектирования. В результате итерационного изменения параметров накатного зубчатого колеса удалось более чем в два раза повысить плавность хода передачи.