Исследование кинематических возможностей зубчато-рычажного механизма с квазиостановками

ЗУБЧАТО-РЫЧАЖНЫЙ МЕХАНИЗМ, ЭПИЦИКЛИЧЕСКИЙ МЕХАНИЗМ, КВАЗИОСТАНОВКА, ЭПИЦИКЛОИДА

Предметом исследования является зубчато-рычажный планетарный механизм с квазиостановкой.

Целью статьи служит определение кинематических возможностей зубчато-рычажного планетарного механизма с квазиостановкой, необходимых для подтверждения целесообразности его использования в конструкции машин легкой промышленности.

В статье представлен расчет геометрических характеристик петли эпициклической траектории движения точки звена зубчато-рычажного механизма, позволяющей обеспечить приближенную остановку исполнительному органу. Дан сравнительный анализ различных математических способов определения поперечного и продольного размеров петли эпициклоиды, служащих основанием для расчета длительности и качества квазиостановки исполнительного органа.

Результаты расчета доказывают достижение необходимых для технологических процессов легкой промышленности длительности и качества квазиостановки, обеспечиваемой планетарном механизмом, что позволяет рекомендовать его к использованию в конструкции машин отрасли.

СОСТОЯНИЕ ПРОБЛЕМЫ

В машинах текстильной и легкой промышленности существуют технологические процессы, которые требуют остановок исполнительного органа определенной продолжительности. Для получения остановки (остановок) исполнительного органа в ходе его рабочего или холостого ходов используются различные способы ее обеспечения. Точную остановку обеспечивают электрон-

MECHANISM TOOTH-LEVER, MECHANISM PLANETARY, EPICYCLE MECHANISM, EPICYCLOID, QUASISTOP

The aim of this article is the investigation of kinematic features of tooth-lever mechanism with quasistop. The subject of the article is the faltering rotary movement mechanism with external toothing wheels.

The article describes the necessity for stops executive bodies of machines of light industry. The calculation of the geometric characteristics of the loop epicycle motion path point of the link toothlever mechanism performed to ensure approached a stop to the executive body. A comparative analysis of various mathematical methods for determining the transverse and longitudinal dimensions of the loop epicycloid that serve as the basis for calculating the duration and quality of quasistop executive body. The calculation results demonstrate the achievement of the necessary process of light industry duration and quality of quasistop provided by the planetary mechanism, which can be recommended for use in construction machinery industry.

ные программоносители, включающие в себя шаговый привод с микропроцессорным управлением. Практика допускает ввиду большой податливости обрабатываемых материалов (текстильные материалы, кожа, кожеподобные материалы и тому подобные) приближенную остановку (квазиостановку): исполнительный орган в это время получает некоторое перемещение, которое не влияет на качество выполне- ния процесса. Ввиду этого, то есть при отсутствии строгих требований к точности остановки, целесообразнее использовать менее дорогостоящий способ ее организации, а именно механический программоноситель, представляющий собой механизм рычажного или зубчатого-рычажного типа.

Исследование кинематических возможностей механизмов с квазиостановкой до сих пор не утратило актуальности и является объектом изучения многих ученых [1, 2], работающих в области теории механизмов и машин. Расчет длительности и качества квазиостановки в большинстве случаев ведется приближенными способами, в связи с чем назрела потребность в решении задачи исследования кинематических возможностей зубчато-рычажного механизма планетарного типа более точными способами.

ЦЕЛЬ РАБОТЫ И ЗАДАЧИ

Целью представленной работы является определение длительности и качества квазиостановки зубчато-рычажного планетарного механизма, доказывающее целесообразность применения механизма в конструкции машин легкой промышленности. В ходе достижения поставленной цели ведется определение геометрических характеристик петли – участка траектории точки звена механизма, обеспечивающей квазиостановку исполнительного органа машины.

МЕТОДИКА ПРОВЕДЕННЫХ ИССЛЕДОВАНИЙ

Методика проведенных исследований опирается на известные алгебраические методы кинематического анализа рычажных механизмов с применением способов разложения в ряды и итерации.

АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

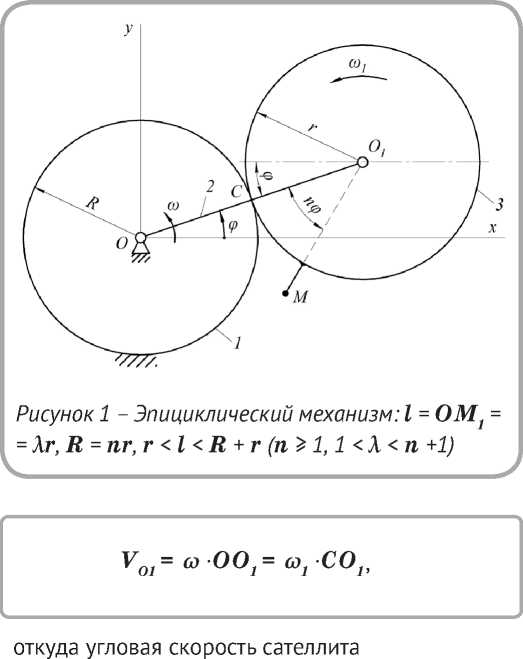
На рисунке 1 изображен эпициклический механизм (элементарная планетарная передача [3, с. 68]), состоящий из неподвижного (заторможенного) центрального колеса 1, водила 2 и сателлита 3 с жестко связанной с ним точкой Ì ( n +1 >  λ > 1), число n = R / r – целое.

При качении без скольжения сателлита 3 по центральному колесу 1 мгновенный центр скоростей сателлита совпадает с точкой контакта колес Ñ . Скорость подвижного конца водила

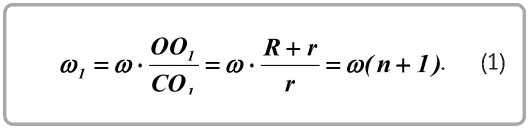
Умножая обе части соотношения (1) на время t , придем к соотношению углов поворота водила и сателлита

Ф1 = ф (n + 1), которое дает (рис. 1) угол поворота сателлита относительного водила:

1 M = ф 1 - ф = Пф

(считаем, что в начальном положении при φ = 0 точка Ì принадлежит оси x , находясь между центрами Î и Î₁ ). Положим угол (2) равным 360°, соответствующий угол φ = 360° / n , то есть за один оборот водила точка Ì окажется на подвижной линии центров ÎÎ₁ между центрами n раз – в эпициклоиде (траектории точки Ì ) образуется n петель.

Параметрическое уравнение траектории

	х = ОО, cos ф — ОМ, cos( п + 1)ф = = (R +г) cos ф-l cos( п + 1)ф = = [/ + 1) cos ф- X cos( п +1 )ф]г, У = [(п + 1) 8Шф-Х81П(п+1 )ф\.	(3)

Угловой коэффициент касательной к эпициклоиде (3), исходящей из начала координат Î ,

	dy У .	(4)
	dx х

Дифференциалы координат (3) в уравнении (4)

dx = [- (n +1) sin ф + X( n +1) cos( n + 1 )ф\п1ф, dy = \(n + l)cos ф—X(n + 1)cos(n + 1 )ф}fdф.

	tgp=— хм	(7)

(приводятся в таблице 1).

Рассмотрим одну из петель, например, ту (рисунок 2), ось симметрии которой совпадает с осью x .

Углы поворота водила, отвечающие точкам M ´ и Ì ´´ петли, находим из уравнения (3), полагая ординату y равной нулю:

	ф 1 + (п + 1) sinф - Xsin (n + 1) ф = 0.	(8)

Разлагая функции sinф и ^т(п+1)ф в степенные ряды и удерживая в рядах по три члена, напишем

Уравнение (4) приобретает вид:

cos ф- X cos( п + 1)ф _ sin ф — X . z ----sin( п + 1)ф п + 1__________ - sin ф + X sin(п + 1)ф COS ф — X — cos( п + 1)ф п + 1 или f Я cos2 ф- AA--cosf ПА- 1)фСО8фА--COS2 (п + 1)ф-

V n+1)n+1

A2

A d--\sin(n + 1)ф sin ф--sin2 (n + 1 )ф, n + 1)                 n + 1'

1 + ^ ^ - ^2 + ^ ^[sinf п + 1)ф sin ф + cos( п + 1)ф cos ф\ = 0,

A2 (1

(5) n + 1       n + 1)

Решение уравнения (5)

1 + п + X2 COS Пф =-------- (2 + п)Х дает углы поворота водила

Ф1 = ± ф (таблица 1), ф2 = ф1 + 2к/ n,..., фп = Ф1 + (п - 1) 2п /n»(6)

отвечающие точкам касания Ì прямых ÎÌ к петлям эпициклоиды (3). Угловые коэффициенты tgp прямых ОМ находятся из уравнения (4)

•^^ ф

Slnф~ф- -—Н,

3!5!

• /                 ф³(п + 1)³  ф⁵(п+1)⁵ /пх

. (9)

Подставим разложения (9) в уравнение (8):

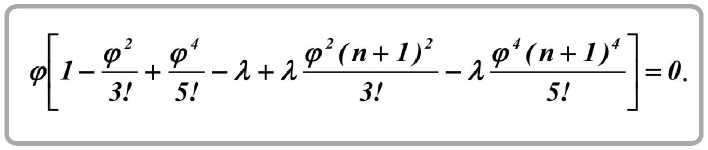
Отметив очевидное решение ф = ф ' = 0, найдем другое решение, полагая его отличным от нуля.

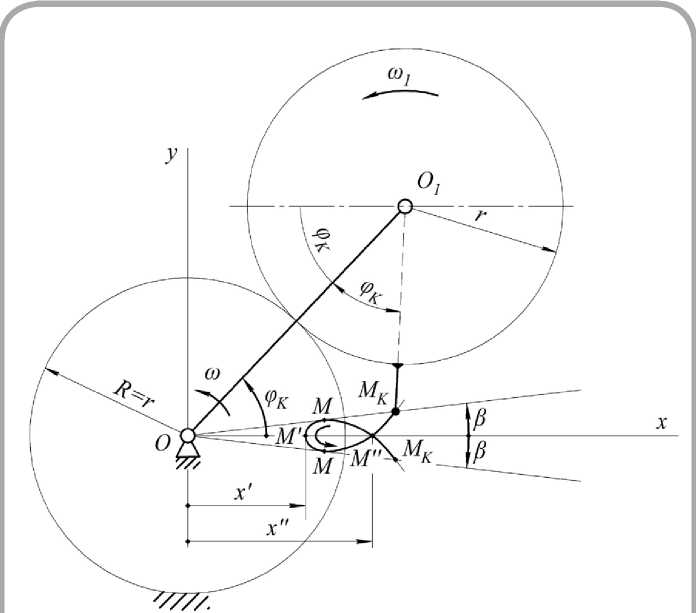
Рисунок 2 – Петля эпициклоиды

Оно найдется из биквадратного уравнения

(n+l)4-l 4 Jn^iy-1 2 , , z.

. (10)

5/                  31

I tge | хмк у Мк.

Прибегая в нем к функциям φ (3), получим уравнение

Если удержать в рядах (8) по два члена ряда, получим квадратное уравнение

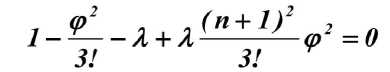
с решениями

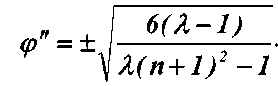
Подстановка решений (12) уравнения (11) в правую часть уравнения, полученного из исходного уравнения (8),

ф" = arcsin

----sin( и + 1 )ф" п + 1

дает при λ = 1,2 значения φ ´´ в левой части, отличающиеся от решений (12) на 1,7 % (при n = 1), 1,3 % (при n = 2), 1,1 % (при n = 3), 1,1 % (при n = 4).

Использование биквадратного уравнения (10) дает большую точность: значения φ ´´ отличаются друг от друга на 0,17 % (при n = 1), в дальнейшем они практически совпадают.

Подстановка значений ф1 (6) в зависимость у ( ф ) (3) позволяет оценить поперечник петли; подстановка значений φ ´ = 0 и φ ´´, найденных из биквадратного уравнения (10), в зависимость x ( ф ) (3) позволяет найти продольный размер петли. Эти размеры (рисунок 2) приведены в таблице 1. С ростом числа петель их длины (выраженные через радиус сателлита) растут, поперечники убывают.

Угол поворота водила ф_к , отвечающий следованию точки М вдоль полупетли М ' ММ"М_к , заключенной внутри угла МОМ (2 в ), находится из равенства

Трансцендентное уравнение (14) решаем способом итерации [4, c. 454]: беря в качестве начального угол φ ´´, подставляем его в правую часть уравнения, определяем слева второе приближение к искомому корню. Подставляя второе приближение в правую часть уравнения, находим третье приближение и так далее. Как только приближения становятся достаточно близкими, вычисления прекращаются (табл. 1).

Угол поворота водила, отвечающий квазиостановке точки М сателлита - следованию точки М вдоль петли М_кМ"ММ ' ММ"М_к , равен 2 ф_к (табл. 1). Деля его на угловую скорость водила, найдем время квазиостановки:

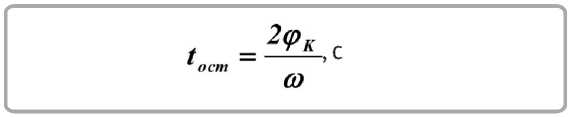
ВЫВОДЫ

В статье даны результаты более строгого определения длительности и качества квазиостановки зубчато-рычажного планетарного механизма, доказывающие возможность и целесообразность его применения в машинах текстильной и легкой промышленности.

ВЕСТНИК ВИТЕБСКОГО ГОСУДАРСТВЕННОГО ТЕХНОЛОГИЧЕСКОГО УНИВЕРСИТЕТА выпуск 28

Таблица 1 – Угловой, поперечный, продольный размеры петли и угол поворота водила, отвечающий «концу» петли

λ	n	| ф 1 |/| ф 1 °| (6)	| tge | (7)	| в °|	2| в °|	21 У м । (3) (рис. 2)	• φ	x ' / r (3)	φ	x "/ r (3)	(x"-x ' ) / r (рис. 2)	Фк (рис. 2)
	1	0,299 17,1	0,0939	5,4	10,8	0,173	0	0,8	0,587	1,201	0,401	0,717
1,2	2	0,195 11,2	0,0433	2,5	5,0	0,168	0	1,8	0,362	2,246	0,446	0,434
	3	0,145 8,3	0,0269	1,5	3,0	0,159	0	2,8	0,265	3,274	0,474	0,313
1___	4	0,116 6,6	0,0200	1,1	2,2	0,158	0	3,8	0,210	4,293	0,493	0,246