Исследование кинетики конвективной сушки натуральных кож

Сушка натуральных кож является сложным комплексным технологическим процессом, в котором шкура, прежде чем превратиться в промышленную кожу, проходит ряд разнообразных операций, важнейшей из которых является дубление [1, 2, 3]. Следует отметить, что натуральная кожа является очень сложным и неоднородным материалом как в отношении толщины, так и в отношении своих различных физико-механических и теплофизических показателей. Влияние на эти показатели оказывает не только возраст и вид животного, но и значительное различие в строении кожной ткани для разных участков шкуры. Поэтому наблюдаются значительные колебания плотности даже для одного вида кожи в зависимости от топографического участка шкуры, из которого вырезан образец кожи [2]. При этом кожа после дубления резко изменяет свои теплофизические константы, присущие шкуре [1, 2].

Например, для краснодубной юфти по данным эксперимента [2] обнаружено колебание плотности сухой кожи р0 от 400 до 560 кг/м3, для стелечного полувала - от 550 до 650 кг/м3, для рантовой подошвы - от 880 до 980 кг/м3. Натуральная кожа относится к термочувствительным материалам, и поэтому сушка проводится при мягких температурных режимах теплоносителя tc = 30-60 °C, скорости v = 0,5-2 м/с и высоких влагосодержаниях воздуха ф = 40-60 %. В процессе сушки кожа на протяжении всего процесса испытывает усадку, при которой значительно изменяются размеры, вызывающие коробление и разрушение структуры материала [1, 2, 3]. Основным препятствием для быстрой интенсивной сушки кожи при повышенных температурах является усадка, коробление и разрушение структуры материала, и поэтому выбор рациональных режимов сушки, обеспечивающих минимальную длительность сушки при высоких технологических качествах готового продукта, имеет важное значение [3]. При мягких режимах сушки кожи наблюдаются периоды постоянной температуры, на уровне температуры мокрого термометра. Основная трудность при экспериментальных исследованиях кинетики сушки в лабораторных условиях заключается в адекватном воспроизведении условий, имеющих место в сушильной установке [4]. Для уменьшения этого несоответствия при исследованиях кинетики все кривые сушки и температурные кривые систематизируются по режимам, последовательно по температурам, скоростям и влагосодержаниям в широком диапазоне изменения режимов сушки и влагосодержаний материала [4].

ОСНОВЫ РЕГУЛЯРНОГО РЕЖИМА

Наиболее общим признаком начала регулярного режима нагрева тела является соотношение [5, 6]

градиенты температуры и при отсутствии в материале термического переноса вещества при значениях Bi < 0,1 (практически достаточно Bi < 0,4) темп нагрева тела определяется уравнением [5–7]

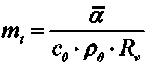
где α — коэффициент теплообмена; c_o — удельная теплоемкость сухого тела; ρ₀ — плотность; R _v — отношение объема тела к его поверхности испарения (характерный размер влажного материала).

При таких условиях теплообмена относительная избыточная температура определяется выражением [6]

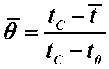
= exp(-Bi • Fo)

Здесь Bi — теплообменный крите р ий Био; Fo — теплообменный критерий Фурье; θ — среднеинтегральная относительная температура.

Учитывая, что Bi ^• Fo = m_t ^• τ_II [6–7], уравнение (3) принимает вид

,

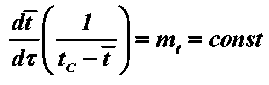
где m_t — темп нагрева материала; dt/dτ — скорость н а грева влажного тела; t_c — температура среды; t — среднеобъемная температура материала.

Темп нагрева материала находится экспериментально построением графической зависимости между ln(tc— t) и временем τ. В стадии регулярного режима такие графики имеют вид прямых. Темп нагрева тела зависит от формы тела, теплофизических характеристик, условий теплообмена поверхности тела с окружающей средой и не зависит от режима сушки. Для тонких плоских материалов при Bi < 1 mt не зависит от толщины материала [5]. При нагревании тонких плоских влажных материалов при мягких режимах сушки наблюдаются незначительные где τII — время сушки во втором периоде. Стадия регулярного режима наступает с началом второго периода сушки. Средняя температура материала в периоде постоянной скорости сушки t0 при малых градиентах температур приближенно равна температуре мокрого термометра tMT = tÏ = t0, где tÏ — температура поверхности материала [9]. Среднеобъемная температура во втором периоде вычисляется из уравнения (4)

~          7        7—                       , (5)

exp(mt • тп ) exp( mt-Tn)

где t0 — температура материала в периоде постоянной скорости сушки; tMT — температура мокрого термометра.

Сушка тонких плоских материалов протекает с периодом постоянной температуры в периоде постоянной скорости сушки, и температура материала в этом периоде равна температуре мокрого термометра t_MT . При сушке таких материалов, когда можно пренебречь градиентом температуры по сечению тела, можно приближенно допустить равенство среднеинтегральной температуры в первом периоде сушки t₀ ≈ t_MT [9]. Плотность потока тепла на нагрев влажного тела при конвективной сушке определяется балансовым уравнением теплообмена [8, 9]

--------------------------------------------------\

_    — Go di q=a(t —t )=c ™- — ,   (6)

c * F dr где F — поверхность испарения материала; G0 — сухая масса материала, cw — удельная теплоемкость влажного тела. Тогда запишем

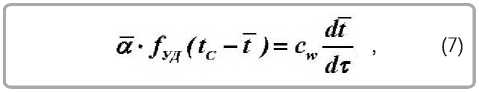
где f _ÓÄ = F / G₀ — удельная поверхность тела.

Удельная поверхность материала выражается соотношением

,

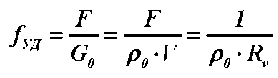
Вывод уравнения (10) согласуется с решением (5), что подтверждает справедливость уравнения (4) для среднеинтегральной температуры материала при условии Bi < 1 для тонких тел.

Основное уравнение кинетики сушки [3, 8, 9] запишем в виде q = in = c 7 =^ (1 + Rb), (11) Qi акр (^c ^mt )

где q ^* — относительная плотность теплового потока; q_I и q_II — плотности потока тепла в первом и втором периодах сушки; α _KP — коэффициент теплообмена в периоде постоянной скорости сушки; Rb — число Ребиндера; N ^* — относительная скорость сушки.

Число Ребиндера

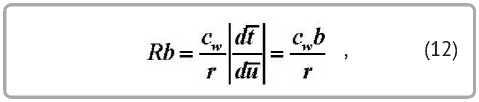
где b — температурный коэффициент сушки, b = d t / d u ; d t / d u — скорость изменения вла-госодержания; r — теплота парообразования.

Число Ребиндера позволяет расчет теплообмена свести к расчету влагообмена. Температурный коэффициент сушки b = d t / d u находится графическим дифференцированием температурной кривой — t = f ( u ) .

Для многих материалов зависимость числа Rb от влагосодержания выражается эмпирической формулой [3, 8, 9]

где V — объем влажного материала.

Р е шением уравнения (7) при начальном условии t(0) = t₀ = t_ÌÒ (начало второго периода) получим уравнение температурной кривой [8]

Rb= A* exp(—n₀ (u — u_p)) . (13)

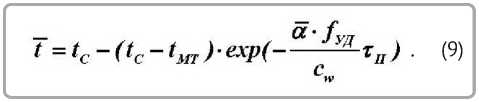
Подставляя (8) в (9) с учетом (2), получим

Постоянные A и n₀ определяются экспериментально.

На основании (12) и (13) для среднеинтегральной температуры можно записать [8, 9, 11]

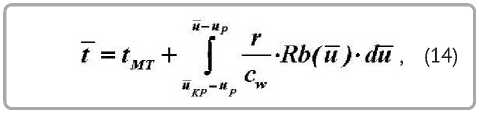
Интегрируя уравнение c учетом (13) для фиксированных значений температуры и влагосо-держания, получим t =tMr + -^- {^[-«s (« - Up) -

.           (15)

Обработкой экспериментов по сушке различных видов натуральной кожи по уравнению (13) методом наименьших квадратов получена формула [7, 11]

. (16)

ЭКСПЕРИМЕНТ

Первичный материал для исследования сушки натуральных кож в виде кривых сушки и температурных кривых заимствован из монографии А. В. Лыкова [2] по многочисленным опытным протоколам наблюдений. Все опыты систематизированы по температурам, скоростям движения и относительным влагосодержаниям воздуха. Обработка эксперимента проводилась: по температурам tC = 40; 50; 60 °C; скорости воздуха v = 0,5; 1; 3 м/с; по влагосодержаниям воздуха φ = 30; 45; 50; 60 %. Большой диапазон изменения режимов сушки при различных начальных влагосодержаниях кожи позволяет получить достаточно достоверные уравнения для расчета основных параметров кинетики сушки. На рисунке 1, 2 и 3 изображены кривые сушки u = f(т) и температурные кривые t = f(т) в процессах сушки краснодубной юфти (рисунок 1), хромового опоека (рисунок 2) и рантовой подошвы (рисунок 3) при различных режимах.

Видно, что при конвективной сушке тонких материалов наблюдаются не только периоды постоянной скорости сушки, но и периоды постоянной температуры на уровне температуры мокрого термометра t_MT ≈ t_Ï . С началом второго периода скорость сушки убывает, а температура непрерывного возрастает до t_c при τ → ∞ . На ри с унке 3 б дана графическая зависимость ln ( t_c — t ) от времени сушки τ для рантовой подошвы, из которой определяется темп нагрева влажного тела m_t . Такие зависимости имеют вид прямых, и следовательно кривые сушки и темпе-

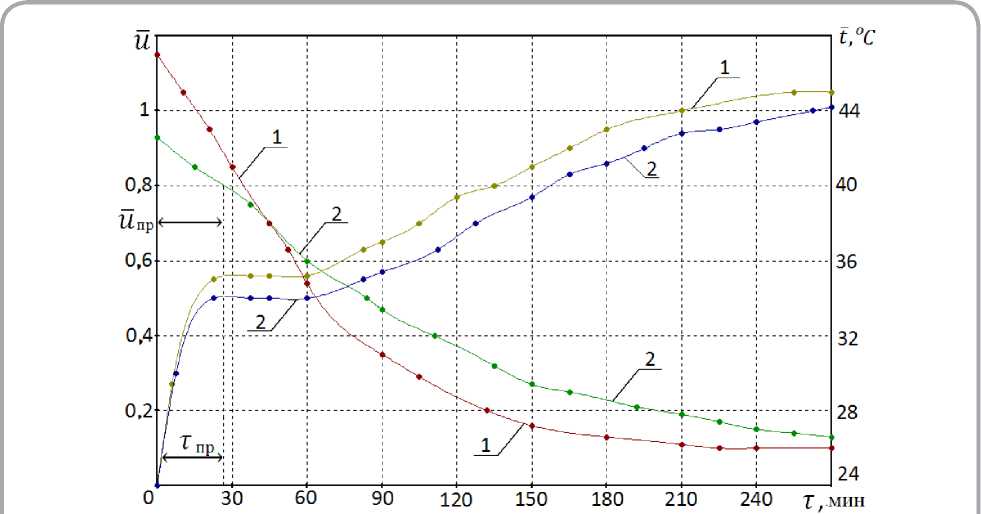
Рисунок 1 - Кривые сушки u = f (т) и температурные кривые t = f (т) для процессов конвективной сушки краснодубной юфти при режимах: 1 — t c = 50 °C ; v = 1 м/с ; ф = 45 % ; 2 — t c = 50 °C ; v = 0,5 м/с ; ф = 50 %

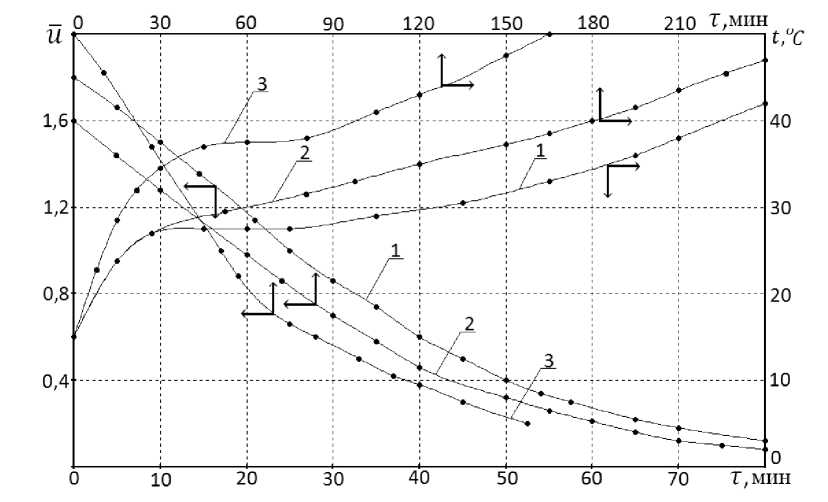
Рисунок 2 - Кривые сушки u = f (T) и температурные кривые t = f (T) для процессов сушки хромового опоека при режимах: 1 — t c = 45 °С ; v = 1 м/с ; ф = 27,5 % ; 2 — t c = 50 °С ; v = 1,5 м/с ; ф = 30 % ; 3 — переменный режим сушки: до й_кр = 1; t c = 60 °С ; ф = 50 % ; от и_кр = 1 до u = 0,22; t c = 45 °С ; ф = 30 % . Скорость воздуха v = 0,5 м/с

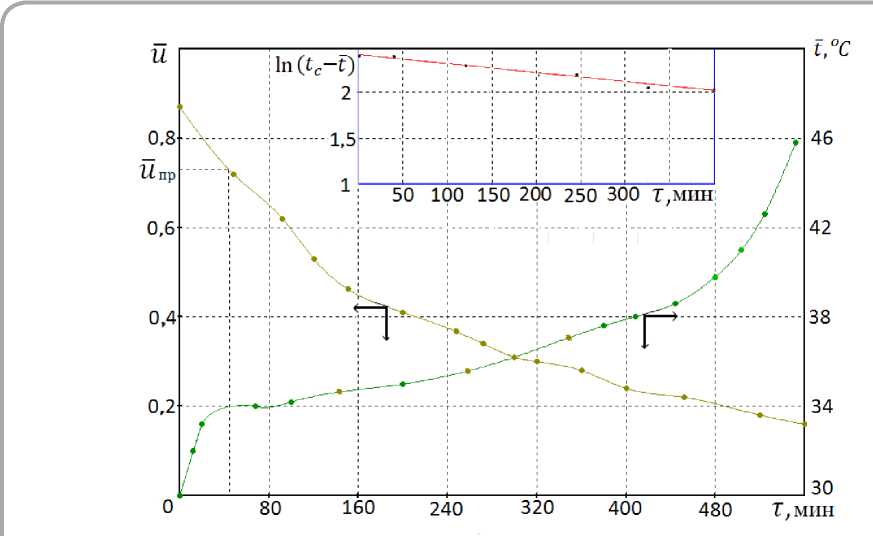
Рисунок 3 - Кривые сушки рантовой подошвы u = f(т) и температурная кривая t = f(т) в режиме сушки: tc = 50 °С; v = 0,5 м/с; ф = 50 % ратурные кривые во втором периоде представляют экспоненты. Стадия регулярного режима наступает сразу с началом второго периода, и распределение температуры внутри тела описывается экспоненциальной функцией и не зависит от начального распределения температуры. В стадии регулярного режима коэффициент неравномерности распределения температуры в теле Ψ = 1; происходит быстрое выравнивание температур по поверхности и объему [5]. Из теории регулярного режима следует, что чем меньше значение критерия Bi, тем быстрее все точки тела по объему вступают в стадию регулярного режима [5, 6].

Обработкой большого числа опытных данных по сушке юфти, рантовой подошвы, опоека, стелечного полувала в широком диапазоне изменения режимных параметров установлена приближенная зависимость для темпа нагрева кожи т, = 0,03-exp(—0,05(WKp - Wp)) , (17)

где W_P и W_KP — равновесное и критическое вла-госодержание материала в процентах ( % ).

КИНЕТИКА ТЕПЛООБМЕНА

Поскольку экспериментальных критериальных уравнений для расчета коэффициента теплообмена α еще не существовало, А. В. Лыковым [2] для определения α на основе обработки опытных данных кривых сушки и температурных кривых была получена формула

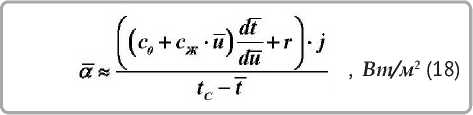
где j — интенсивность испарения влаги с поверхности материала; c_Æ — теплоемкость жидкости.

Среднеобъемная температура кожи t для каждого текущего влагосодержания материала определялась по температурной кривой t = f(u). Скорость возрастания температуры dt / du находится графическим дифференцированием кривой t = f(u). Величина dt / du в дальнейшем была названа А. В. Лыковым температур- ным коэффициентом сушки [3]. Формула (18), полученная для натуральных кож, справедлива до сушки u ≈ 0,25, поскольку при u < 0,25 происходит углубление зоны испарения и значительная часть тепла идет на нарушение связи влаги с материалом, и величина r не соответствует действительности. В таблице 1 даны расчеты коэффициента теплообмена α для процесса сушки краснодубной юфти при различных режимах по данным А. В. Лыкова [2] и сравнение этих значений α, вычисленных по-современному критериальному уравнению [1, 3, 9]. Обработкой большого количества экспериментальных данных по конвективной сушке различных материалов была установлена формула для теплообмена критерия Нуссельта [3, 8–10]

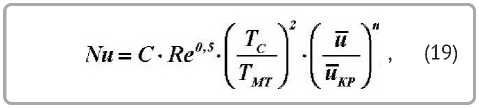
где Re — критерий Рейнольдса; T_C и T_MT — абсолютные температуры среды и мокрого материала.

Постоянная n учитывает уменьшение коэффициента теплообмена α в периоде убывающей скорости сушки. Проведена обработка опытных данных по сушке различных видов натуральной кожи в широком диапазоне изменения режимных параметров сушки с целью сопоставления полученных результатов с показателями в формуле (19). На рисунке 4 приведены результаты обработки экспериментов для зав и симостей lgNu = f (lgRe) и lg( α / α_KP) = f (W / W_KP) для различных кож при разных режимах сушки. Показатель степени в критерии Рейнольдса полностью совпадает с принятым в уравнении (19). Постоянная n = 0,75 для всех видов натуральной кожи. Коэффициент Ñ , определяемый уравнением C = Nu / Re ^0,25 , оказался равен Ñ = 0,95. Показатель степени в симплексе (T_C / T_MT) , определяется из зависимости lgNu / Re ^0,25 = f (lgT_C / T_MT) и также практически совпадает с принятым значением в уравнении (19).

В таблице 1 дано сопоставление значений коэффициентов теплообмена по формуле А. В. Лыкова с вычисленными по критериальному уравнению (19). Отмечается явное совпадение расчетных значений α .

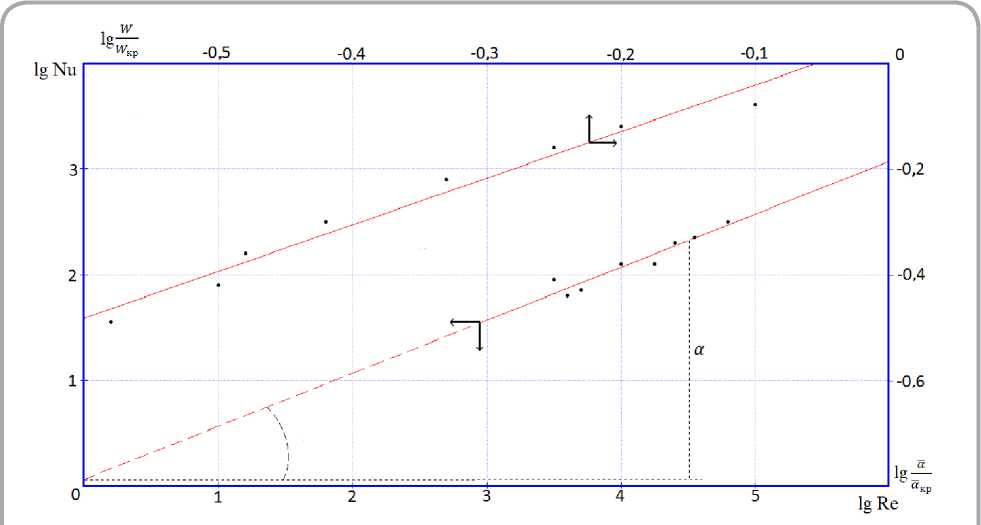
Рисунок 4 - График зависимости lgNu = f (lgRe) и lg(W / W KP ) = f ( lga / a KP ) для процессов конвективной сушки натуральных кож при различных режимах сушки (режимы указаны на рисунках 1, 2 и 3)

Таблица 1 – Зависимость коэффициента теплообмена α от влагосодержания краснодубной юфти в процессе конвективной сушки при различных режимах

t c , °С	40	40	50	50	50	50	60	60	50
φ , %	40	60	80	40	45	45	45	45	45
v, м/с	0,5	0,5	0,5	0,5	0,5	3	4	0,5	1
W , %	Коэффициент теплообмена a , Вт/м2 ^ °С ,числитель (15), знаменатель (16)
80	11,5	8,3	5,4	11,5	10,5	27,5	30	14,8	17,1
	10,4	9,4	4,6	10,8	9,5	25,4	28,6	12,6	16,7
70	11,2	8,1	5,8	11	10,8	27,3	30	14,7	17,1
	10,4	9,3	4,8	10,8	10,2	25,4	28,6	12,6	16,7
60	9,2	7,2	4,2	11,5	9,6	27	27	13,5	13,6
	9,6	8,3	3,8	10,3	10,5	25,2	27,2	11,8	14,2
50	8,8	6,5	3,9	9,6	8,9	25	24,5	10,9	12,8
	8,6	7,2	3,4	8,9	9,2	23,3	23,7	10,3	13,2
40	7,9	5,7	2,9	8,8	8,6	23	22,6	9,8	11,6
	7,3	6,2	2,7	7,7	8,4	21,2	20,3	8,8	11,2
30	7,3	5,8	2,5	7,8	7,2	19,5	18,4	8,4	9,8
	5,9	4,6	2,2	6,5	6,8	16,7	16,8	6,8	9,1
25 v	6,2	3,1	–	6,5	3,5	16	16,4	6,5	8,1
	5,2	3,9	–	5,4	3,9	13,8	14,7	6,1	7,9

В качестве примера приведем расчет α_KP для периода постоянной скорости сушки для краснодубной юфти по формулам (18) и (19) при режиме: t c = 50 °С ; v = 1 м/с ; ф = 45 % ; u ₀ = 1,13; u _KP = 0,7. Экспериментальные данные по протоколу опыта. Пластина 250*150x1,8 мм ; t MT = t n = 35 °С ; скорость сушки в первом периоде N = 1,5 - 10^-4с ¹ ; скорость изменения температуры dt / du ~ 5 °С при переходе первого периода во второй. Поверхность пластины F = 0,0375 м2 . Объем V = 0,0675 • 10^-3 м3 . Количество удаляемой влаги G_BЁ = 30,6 - 10^-3 кг . Абсолютно сухой вес образца G 0 = 27 - 10^-3 кг . Плотность образца юфти р0 = G 0 / V = 27 - 10^-3/ / 0,0675 - 10^-3 = 400 кг/м³ . Удельная теплоемкость кожи с₀ ~ 1550 Дж/кг - °С .

Интенсивность испарения влаги [3]

Коэффициент теплообмена α _KP равен

	_    Nu-A„  96,9-2,83-IO"2 a =----— = —:---:------= KP     I           0,15
	= 18,2 Вт/м2-°С .	(24)
-

Кинематическая вязкость и теплопроводность воздуха v_B и λ_B определяется по таблицам [4] при t c = 50 °С , l — длина образца кожи по набеганию потока. Плотность теплового потока в первом периоде по уравнению кинетики сушки

х х1,8-10"3 -1,5-Ю"4 = 261 Вт/м2-°С.. (25)

х х1,8-10"3« 1,08# ка/м^с..   (20)

■

Коэффициент теплообмена по формуле

А. В. Лыкова

Коэффициент теплообмена α _KP равен

_ q, 261       , аКР = —— = —— =17,4 Вт/м2-°С. (26)

_   ^1550*4200^-5 * 2420-10^-1,08-10 "4

“КР~             50—35             ~

= 17,6 Вт/м^°С .

Коэффициент теплообмена α _KP по критериальному уравнению (19).

Для периода постоянной скорости сушки отношение ( u / u _KP)^0,75 = 1.

Число Рейнольдса

Плотность потока тепла в первом периоде сушки по уравнению Ньютона

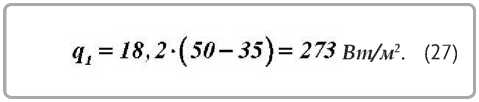
Погрешность при всех методах вычисления α_KP и теплового потока составила Δ ≈ 4,5 % .

Запишем основное уравнение кинетики сушки в виде [3, 8–10]

п V-1	1-0,15
Re =--=	.	(22)
v«	17,8-Ю"6

Коэффициент теплообмена определяется по критериальному уравнению теплообмена для критерия Нуссельта [4]

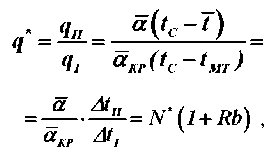
Nu = 0,95• (8427)8’5 •

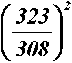
. (23)

где Δ t_I и Δ t_II – изменения температур в первом и втором периодах сушки.

Уменьшение коэффициента теплообмена α в периоде подающей скорости сушки выражается соотношением [3, 8, 10]

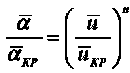
Для процессов сушки всех видов натуральных кож n = 0,75.

На рисунке 5 дана обработка эксперимента для зависимости A t I / A t I = f (u / u KP ) , которая приближенно аппроксимируется уравнением, справедливым для всех видов кож

Из [10], с учетом числа Ребиндера следует

Nu	.	(32)
NuKP	®КР

где Nu KP - критерий Нуссельта в первом периоде.

Учитывая соотношения (29) можно записать

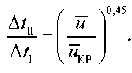
/ _ V®

.        (33)

J1»')

На основании уравнений (28), (29) и (30) имеем

.

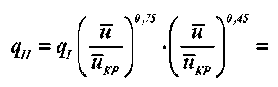
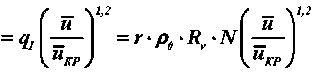
Тогда относительная скорость сушки N * равна

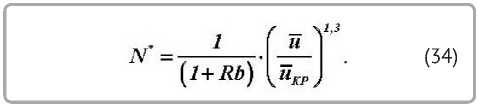
Подставляя в (28) получим

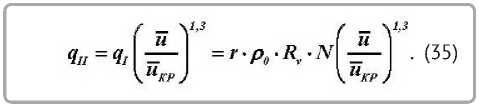
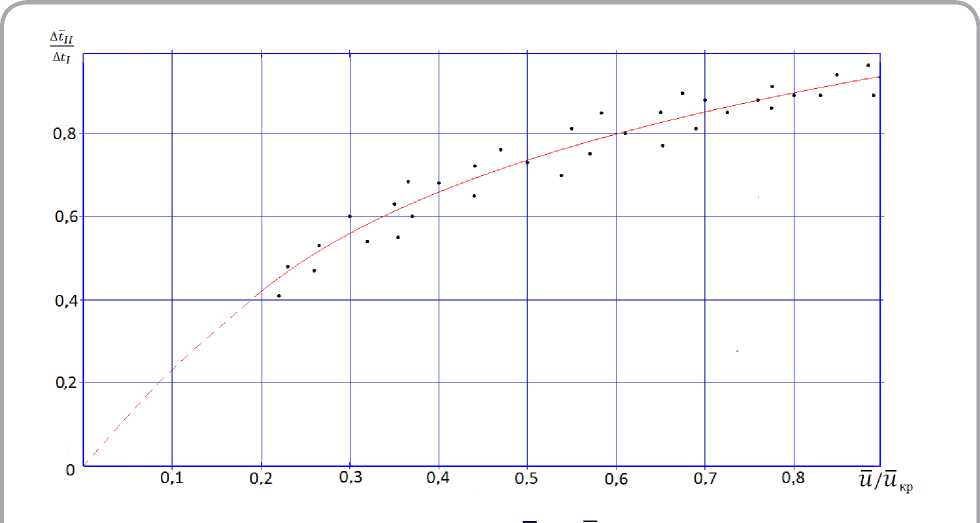
Рисунок 5 – Зависимость отношения температур Δ t _II / Δ t _I от относительного влагосодержания u / u KP для процессов сушки натуральных кож при различных режимах сушки (режимы указаны на рисунках

1, 2 и 3)

Уравнение (32) получено при обработке большого числа экспериментов по сушке более 13 наименований различных материалов, а (31) обработкой эксперимента по конвективной сушки различных видов натуральных кож. Следует отметить, что конвективная сушка натуральной кожи проходит при мягких режимах ( t_c = 30— 60 °C ) , скоростях воздуха v = 0,5 — 1,5 м/с и высоких относительных влагосодержаниях воздуха Ф ( ф 40—80 % ). При таких условиях сушки процессы являются малоинтенсивными.

Пример. Приведем расчет значений плотностей тепловых потоков для второго периода сушки по формулам (31) и (35) для режима сушки краснодубной юфти. Режим сушки: t c = 50 °C ; v = 1 м/с ; ф = 55 % ; и₀ = 1,13; u KP = 0,7 ; u₀ = 0,7; U p = 0,12; N = 1,5 • 10^-4 c ¹ ; q , = r • p0 • Rv • N = = 2420 • 10 3 • 400 • 1,8 • 10^-3 • 1,5 • 10^-4 = ~ 261 Вт/м² .

Максимальная погрешность в значениях тепловых потоков, вычисленных по формулам (31), (35) составляет около 8 % только при влагосо-держаниях близких к равновесным, но находится в пределах точности проведения эксперимента.

Обозначим dt / dT через b' и запишем уравнение (1) в форме изображены зависимости b' = mt • (tc — t) = = f(u / uK-P), полученные обработкой эксперимента по сушке рантовой подошвы, краснодуб-ной юфти и хромового опоека при различных режимах. Эти зависимости приближенно аппроксимируются уравнением b' = dt/dr = mt(tc -1 ) = D~

u

< ^ukp 7

x»,45

. (37)

Обработкой опытных данных получены значения параметра D ( °С/с ), которые определяются видом натуральной кожи и не зависят от режима сушки: рантовая подошва — D_paht = 6 • 10 -4 ; краснодубная юфть — D_ЮФTЬ = = 4,6 • 10^-4; хромовый опоек — D_on = 1 • 10^-4.

Решением уравнения (37) вычисляется среднеинтегральная температура кожи во втором периоде сушки

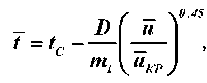
где m_t — темп нагрева, c^-1 .

Подставляем (30) в (37), получим

,          (36)

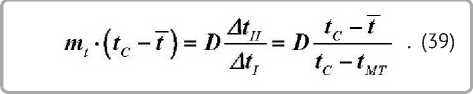
где b' — скорость изменения температуры во втором периоде сушки за единицу времени, определяемая графическим дифференцированием температурной кривой t = f ( T ) . На рисунке 6

После простых преобразований получим выражение для определения температуры мокрого термометра

Таблица 2 – Результаты расчета значений плотностей тепловых потоков для второго периода сушки для режима сушки краснодубной юфти
u	0,65	0,6	0,5	0,4	0,35	0,3	0,25
u / u KP	0,928	0,875	0,714	0,571	0,5	0,428	0,375
q II , Вт/м2 (31)	238,4	216,5	143,6	109,4	92,8	77,3	61,6
q II , Вт/м2 (35)	236,8	213,6	139,4	105,2	87,7	71,6	56,8
Л , % разбежка	0,84	0,93	2,8	3,6	5,3	6,5	7,9

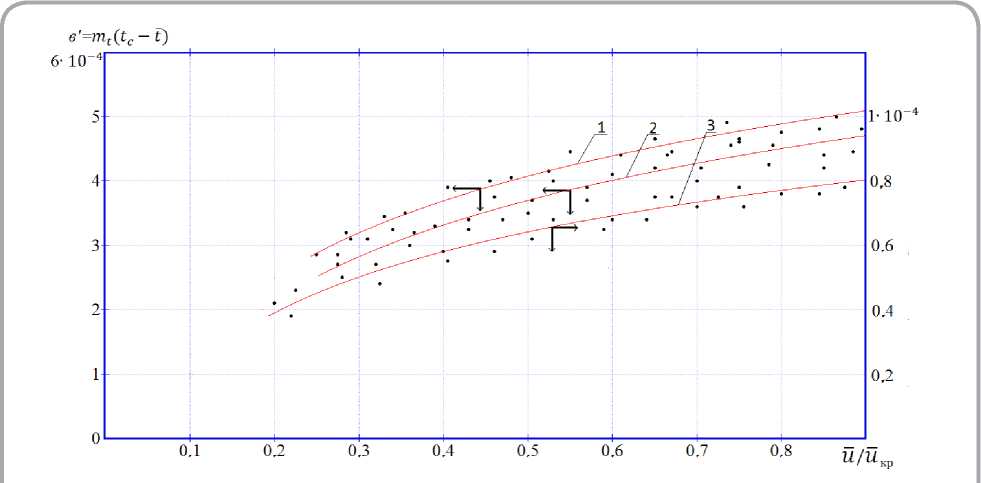
Рисунок 6 - Зависимость b' = m t • (t c — t) от относительного влагосодержания материала для различных видов кож при разных режимах (режимы указаны на рисунках 1, 2 и 3):

1 — краснодубная юфть; 2 — хромовой опоек; 3 — рантовая подошва

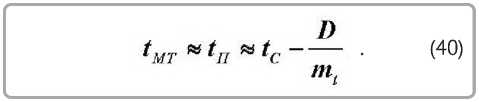
кинетики сушки результаты аналитических решений уравнений теплопереноса. Для бесконечной неограниченной пластины при граничных условиях третьего рода, нагреваемой в среде t_c = const , когда теплообмен между ограничивающими поверхностями пластины с окружающей средой происходит по закону Ньютона, при значениях теплообменного критерия Bi < 1 А. В. Лыковым [5] получено уравнение для избыточной температуры на поверхности материала

. (43)

^C ~ ^H

Для процесса сушки рантовой подошвы при режиме: t c = 50 °C ; v = 0,5 м/с ; ф = 45 % ; u_KP = ^0,6 ; u p = 0,1; t MT _3KC = ³⁴ ° ^C ; m t = ^3,7 • 10^-5 c^-1 .

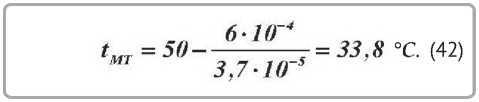
Совпадение расчетных значений t_MT с экспериментальными вполне удовлетворительнoе. Представляет интерес использовать в расчетах

Учитывая, что Bi • Fo = m t T II уравнение (43) примет вид

. (44)

Начальной температурой отсчета для второго периода сушки является температура в периоде постоянной скорости сушки tMT ≈ tÏ. В малоинтенсивных процессах сушки при нагреве тонких плоских влажных тел при tc = const и отсутствии в материале термического переноса вещества градиентом температуры по сечению тела можно пренебречь, и температуру θÏ можно без большой погрешности заменить на среднеинтегральную 0(tn~ t) [6,9]. Анализ большого числа экспериментов на конвективной сушке различных видов натуральной кожи [1, 2] показал, что перепад температуры по сечению влажного материала не превышает At ~ 2—4 °C и зависит от толщины кожи.

Принимая приближенно θ_Ï ≈ θ , расчетное уравнение запишем в виде

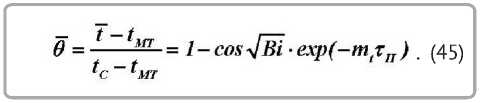
Среднеинтегральная температура определяется выражением

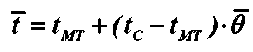
В таблице 3 дано сравнение расчетных значений среднеинтегральных температур, вычисленных по уравнениям (5), (15) и (32), с экспериментом для процесса сушки краснодубной юфти при режиме tc = 50 °C; v = 1 м/с; ф = 45 %. При вычислении величины критерия Bi необходимы достоверные зависимости коэффициента теплопроводности влажной кожи от влагосодержания и температуры материала. С использованием данных, приведенных в [1, 2], по коэффициенту теплопроводности влажных кож и формулы В. И. Дубницкого [3]

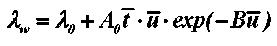
была проведена обработка этих данных. В результате зависимость коэффициента λ_W от температуры и влагосодержания

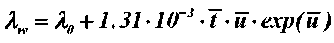
. (48)

Коэффициент B для натуральных кож принимает положительные значения и равен B = 1. Теплопроводность абсолютно сухой кожи равна: рантовая подошва — λ₀ = 0,120; краснодубная юфть — λ₀ = 0,105; опоек хромового дубления — λ₀ = 0,055; юфть танидного дубления — λ₀ = 0,115 Вт/м • °C .

ЗАКЛЮЧЕНИЕ

На основе метода теории регулярного режима проведено исследование кинетики теплообмена для процессов сушки различных видов натуральной кожи. Получены уравнения для опреде-

Таблица 3 – Сравнение экспериментальных значений среднеинтегральных температур с расчетными, вычисленными по уравнениям (5), (10), (15), (38), (44), для процесса конвективной сушки краснодубной юфти в режиме сушки t c = 50 °C ; v = 1 м/с ; ф = 45 %

и	а, Вт/м2 - °C	^w, Вт/м2 - °C	Bi	ТП' мин	t, °C (5), (10)	t, °C (15)	t, °C (38)	9 (44)	t, °C (44)	t, °C эксп.
0,6	13,6	0,170	0,143	12,5	35,4	35,4	35,4	0,086	36,3	35,6
0,5	12,8	0,159	0,144	22,2	35,9	36,2	36,6	0,105	36,7	35,9
0,4	11,6	0,148	0,141	38,2	36,6	37,5	37,8	0,128	36,9	36,8
0,35	10,5	0,143	0,132	55,4	37,0	38,2	38,0	0,135	37,2	37,2
0,3	9,7	0,139	0,126	77,3	37,3	39,4	38,8	0,146	37,5	38,5
0,25	8,1	0,135	0,115	98,8	38,2	–	39,8	0,195	38,3	38,6

Примечание: пластина юфти: 250*150*1,8 мм ; и₀ = 1,13; u_KP ~ 0,7; и_р = 0,12; t_MT ~ t_n = 35 °C ; р₀ = 400 кг/м³ ; с₀ = 1,55 кДж/кг • °C ; Х0 = 0,115 Вт/м • °C ; m_t = 1,76 • 10 -3 мин¹.

ления плотности тепловых потоков и среднеинтегральных температур в периоде убывающей скорости сушки. Установлена зависимость для темпа нагрева натуральных кож. Представлены примеры расчета параметров сушки по приведенным уравнениям. Дана проверка достоверности полученных уравнений и сопоставление расчетных значений температур с экспериментом. Получено приближенное уравнение для вычисления теплового потока без определения коэффициента теплообмена. Рассмотрена возможность применения для расчета среднеинтегральной температуры результата аналитических решений уравнений теплопереноса.