Исследование коэволюционного алгоритма генетического программирования и его применение в задаче моделирования фазовых границ магнитного состояния кристалла

Результаты исследования алгоритма генетического программирования (ГП) показывают, что нельзя однозначно говорить о превосходстве какого-то конкретного алгоритма ГП и даже после многократных решений задачи остается неопределенность в выборе параметров метода ГП [1]. Это подтверждает то, что для каждой задачи существует свой алгоритм с наилучшей стратегией поиска. А выбор конкретного алгоритма и настройка его параметров сами по себе являются очень сложными проблемами.

Для устранения подобных проблем необходимо разрабатывать процедуры, автоматизирующие подстройку параметров ГП в ходе однократного решения задачи. Одной из таких процедур является использование коэволюционных стратегий, т. е. конкуренции алгоритмов ГП за ресурс [2; 3].

Основная идея коэволюционного алгоритма состоит в одновременной эволюции нескольких субпопуляций, каждая из которых решает свою задачу символьной регрессии и обладает своей стратегией поиска (моделирования). При этом субпопуляции борются за общий ресурс, который в течение работы алгоритма перераспределяется в пользу более эффективной из них.

Коэволюционный алгоритм состоит из следующих шагов.

Шаг 1. Выбор индивидуальных алгоритмов.

Шаг 2. Инициализация параметров коэволюцион-ного алгоритма.

Шаг 3. Работа индивидуальных алгоритмов ГП в течение заданного интервала адаптации.

Шаг 4. Проверка критерия остановки: если данный критерий срабатывает, то выводится лучшее найденное решение и алгоритм прекращает работу; иначе – переход на шаг 6.

Шаг 5. Оценка алгоритмов.

Шаг 6. Перераспределение ресурса (на основе оценки, полученной на шаге 5).

Шаг 7. Переход на шаг 3.

Использование в коэволюционном алгоритме конкурирующих стратегий алгоритмов предполагает, что для субпопуляций необходимо ввести функцию пригодности, с помощью которой будет определяться лучшая субпопуляция с предоставлением ей большего ресурса для решения задачи. Пусть Т – интервал адаптации, b(k) = (kT, kT–1, …, k1) – вектор длиной Т. Если i-я популяция в момент k содержит наилучшего (по всем популяциям) индивида, то bi(k) = 1, в противном случае bi(k) = 0. Качество популяции можно оценить по формуле [4]:

т -1 T — k q^ X,,- bi(k). (1) k=0 k +1

Размеры ресурсов изменяются за счет сокращения каждой проигравшей популяции на некоторое число индивидов, т. е. определенный заранее размер штрафа, и увеличения победившей популяции на число, равное сумме потерь проигравших. Таким образом, общее число индивидов остается неизменным. Сокращение проигравших популяций осуществляется только до тех пор, пока они не достигнут минимального гарантированного размера – социального минимума.

В связи с тем что ГП является стохастической процедурой, оценка его эффективности осуществляется усреднением по многократным запускам. В качестве критерия сравнения может быть использован показатель надежности – процент успешных запусков алгоритма от общего числа запусков алгоритма. При этом в состав коэволюционного алгоритма индивидуальные алгоритмы включаюттся случайным образом.

В результате проведенного авторами исследования было выявлено, что коэволюционный алгоритм превосходит все индивидуальные алгоритмы ГП (рис. 1). Происходящий в ходе поиска процесс перераспределения ресурсов между алгоритмами, показанный на рис. 2, подтверждает правильность предположения о том, что нельзя отнимать весь ресурс у алгоритма (выгодность социального минимума), так как проигрывающие на начальных шагах алгоритмы могут в дальнейшем найти лучшее решение.

На эффективность коэволюционного алгоритма могут оказывать влияние следующие параметры: величина интервала адаптации, размер штрафа и размер социального минимума, количество индивидуальных алгоритмов.

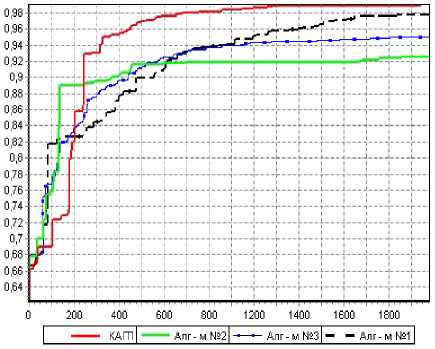
Рис. 1. Пример поведения лучшего индивида: коэволюционный алгоритм ГП показан плошной жирной линией

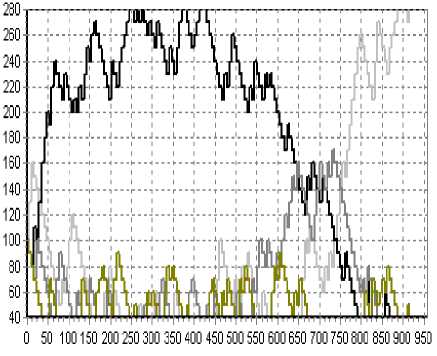
Рис. 2. Пример перераспределения ресурса в ходе работы коэволюционного алгоритма ГП

В ходе исследования было установлено, что использование такого параметра, как размер штрафа, равного некоторому проценту от величины популяции индивидуального алгоритма, неэффективно, так как данная величина является фиксированной и не зависит от количества индивидуальных алгоритмов. Однако такой штраф будет эффективным в случае, когда размер популяции индивидуального алгоритма равен 100 индивидам. Уменьшение или увеличение этой величины отрицательно сказывается на эффективности работы коэволюционного алгоритма.

Для разрешения этой проблемы предложена следующая процедура расчета размера штрафа в зависимости от количества индивидуальных алгоритмов ГП и общего числа индивидов (рис. 3):

Z ₌ r SpCA . zh \ 2- ( N, 2) ,

I 100 )

где Z – количество индивидов, на которое будут штрафоваться проигравшие индивидуальные алгоритмы; SpCA – общее число индивидов; zh – устанавливаемый пользователем размер штрафа в процентах; N – количество индивидуальных алгоритмов.

Размер штрафа

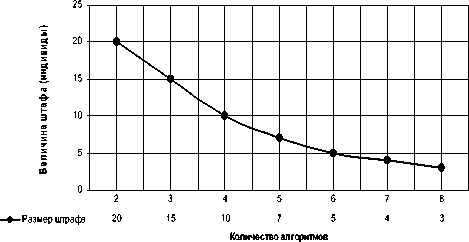
Рис. 3. Функция изменения штрафа в зависимости от количества индивидуальных алгоритмов

Изменение процедуры вычисления размера штрафа привело к тому, что величина социального минимума, как и размер штрафа, также должна зависеть от общего числа индивидов. Поэтому было принято решение устанавливать величину социального минимума как некоторый процент от общего числа индивидов, задаваемого пользователем.

Таблица 1

Результаты исследования зависимости эффективности коэволюционного алгоритма от размеров штрафа и социального минимума

Социальный минимум/штраф, %	2	4	6	8	10	12	14	16
2	15	20	20	5	10	5	20	10
4	10	15	10	20	10	25	10	5
6	5	10	25	20	25	20	15	5
8	15	5	15	15	15	20	5	15
10	20	25	15	20	45	40	20	15
12	10	5	20	25	30	25	15	5
14	15	10	15	10	20	15	15	0
16	0	5	5	10	15	10	5	10

Для того чтобы установить характер зависимости эффективности коэволюционного алгоритма от значений его параметров и выработать рекомендации по их настройке, были проведены:

– исследование эффективности коэволюционного алгоритма в зависимости от величины штрафа и социального минимума (табл. 1);

– исследование зависимости эффективности ко-эволюционного алгоритма от величины интервала адаптации (табл. 2);

– исследование зависимости эффективности ко-эволюционного алгоритма от количества индивидуальных алгоритмов (табл. 3).

Таблица 2

Результаты исследования зависимости эффективности коэволюционного алгоритма от величины интервала адаптации

Интервал адаптации	N 3 , %	N 2 , %	N 1 , %
2	15	75	10
3	10	60	30
4	35	55	10
5	45	50	5
6	25	65	10
7	10	85	5
8	15	75	10
9	5	80	15
10	10	75	15

Таблица 3

Результаты исследования зависимости эффективности коэволюционного алгоритма от количества индивидуальных алгоритмов

Количество алгоритмов	N 3 , %	N 2 , %	N 1 , %
2	15	80	5
3	35	50	15
4	45	50	5
5	40	50	10
6	35	50	15
7	30	50	20
8	20	60	20

Примечание . В табл. 2 и 3 применяются следующие обозначения:

- N ₁ – количество запусков, в которых было получено решение с ошибкой аппроксимации больше 5 %, в процентах от общего количества запусков;

- N ₂ – количество запусков, в которых было получено решение с ошибкой аппроксимации больше 1 %, но меньше 5 %, в процентах от общего количества запусков;

- N ₃ – количество запусков, в которых было получено решение с ошибкой аппроксимации меньше 1 %, в процентах от общего количества запусков.

В табл. 1–3 в качестве примера приведены наиболее информативные результаты тестовой функции sin( x ) на интервале [–3,14; 3,14] со случайным шагом, объем тестовой выборки равен 100 точкам. В качестве функционального множества использовались только арифметические операции (+, –, *, /), терминальное множество содержало переменную x и набор констант на интервале [–1; 1] со случайным шагом.

В результате исследования эффективности работы коэволюционного алгоритма ГП в зависимости от параметров, входящих в его настройку, было установлено, что:

• –    коэволюционный алгоритм ГП всегда лучше самого худшего из алгоритмов и даже лучше чем средний алгоритм по показателям надежности;

• –    коэволюционный алгоритм ГП позволяет автоматически выбирать лучшую стратегию из имеющихся и включать ее в необходимый момент;

• –    не нужно сильно штрафовать (размер штрафа 10…12 %) проигравшие алгоритмы, но в то же время не надо оставлять им больших социальных гарантий;

• –    интервал адаптации необходимо выбирать равным 4…5;

• –    количество индивидуальных алгоритмов должно быть 3…6;

• –    в случае полного отсутствия знаний о предпочтительности выбора индивидуальных алгоритмов даже комбинация из практически неработающих алгоритмов, худших по надежности в сравнении с другими алгоритмами, имеет большую надежность, чем надежность каждого из этих алгоритмов по отдельности;

• –    75 % решений по показателю N 2 имеют ошибку аппроксимации меньше 1,6 %, т. е. коэволюционный алгоритм ГП позволяет получать достаточно хорошие аппроксимации;

  – коэволюционный алгоритм генетического программирования практически на порядок превосходит по скорости нахождения решения метод генетического программирования.

Результаты работы коэволюционного алгоритма ГП с применением предложенных выше настроек представлены в табл. 4. Точное решение в табл. 4 означает, что алгоритм нашел точную структуру заданной тестовой функции.

На основе полученных результатов можно сделать вывод о полезности и перспективности коэволюцион-ного алгоритма, который позволяет автоматически выбирать лучшую стратегию из имеющихся и включать ее в необходимый момент. Однако для подтверждения этого вывода требуется проведение дополнительной проверки на реальных задачах. Одна из них приведена ниже.

Задача построения фазовых границ магнитного состояния кристалла . При решении данной задачи использовались следующие параметры коэволюционного алгоритма генетического программирования: терминальное множество – { x , C }, где x ∈ R , C ∈ [–10;10]; функциональное множество – {+, –, *, ÷, sin, cos, sqrt, power, ln, exp}; размер ресурса – 400; начальная глубина деревьев – 3; интервал адаптации – 5; размер штрафа – 10 %; размер социального минимума – 10; количество индивидуальных алгоритмов – 4.

К сожалению, для антиферромагнетиков даже с достаточно слабым обменом (низкие температуры Нееля TN) обменные поля имеют порядок 1 000 кЭ, а постоянные лабораторные поля достигают величин напряженности на два порядка ниже обменных. Поэтому экспериментальных данных по исследованию поведения двупреломления при изменении магнитной структуры во внешнем магнитном поле для них практически нет. Уникальными являются данные, полученные в импульсных магнитных полях на кристаллах Rb2MnCl4 и NaMnCl3, представленные в [5; 6]. Будучи чувствительными к магнитной структуре, рефрактометрические свойства могут быть использованы для изучения фазового состояния кристалла (рис. 4–6).

Проецируя на плоскость Н - T критическое поле H_SF , при котором наблюдается скачок двупреломления при различных температурах, можно получить линию фазовых переходов первого рода, связанных с опрокидыванием магнитных моментов подрешеток в Rb₂MnCl₄ (рис. 7).

Фазовая граница между антиферромагнитной и парамагнитной фазами лежит в узком температурном интервале. Ожидаемое соотношение, описывающее уравнение границы между антиферромагнитной и парамагнитной фазами, имеет вид

T*Н )/ T n (0) « (1 + у Н 2 )\ (3)

где ^ = 1 (получено в приближении молекулярного поля); Т тр = 49 ± 1,5 К, Н тр = 64 ± 2 кЭ. На этой границе сходятся линии фазовой диаграммы, разделяющие антиферромагнитную, спин-флоп и парамагнитную фазы.

Спин-волновое приближение дает оценку зависимости, описывающей границу между антиферромагнитной и спин-флоп-фазами, в виде H SF « T g , где g = 3/2 – 5/2. Полученная генетическим алгоритмом символьная зависимость (рис. 8) практически неотличима от T ^3/2.

Кривые зависимости двупреломления от магнитного поля и температуры, представленные на рис. 6, можно использовать для построения фазовых границ магнитного состояния NaMnCl 3 . Проецируя критические поля H_c , при которых меняет знак вторая производная д ² ф/д Н² , получим линию Hc ( T ) для критических полей, при которых происходят фазовые переходы из антиферромагнитного в парамагнитное состояние при температуре Т (рис. 9).

Таблица 4

Результаты работы коэволюционного алгоритма ГП

№ п/п	Тестовая функция	Точное решение, %	Е < 0,000 1, %	C ( n )	N
1	f ( x , y ) = x 2 + y 2	100	100	7	10
2	f ( x , y ) = x 2 + y 2 - cos( x ) - cos( y )	75	100	13	116
3	,           A mx ■ m2 F ( mv m 2 , R ) = R	100	100	8	7
4	f ( x , y , z ) = x 2 + y 2 + z 2	100	100	9	33
5	f ( x , y , z ) = x 3 + x ■ y + z 2	100	100	11	76
6	6 f ( x ) = ^ x i = 1	100	100	11	58

Примечание . В таблице использованы следующие обозначения: E – ошибка аппроксимации; C ( n ) – количество узлов в лучшем решении; N - номер поколения, на котором алгоритм нашел решение с заданной точностью. Величина d A n/dT ведет себя как производная термодинамических потенциалов, поэтому по ее аномалиям можно определить точку фазового перехода.

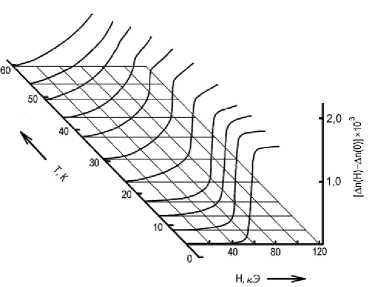
Рис. 4. Зависимость линейного двупреломления Rb₂MnCl₄ при неаксиальном направлении распространения света от магнитного поля H || C ₄ при различных температурах [5]

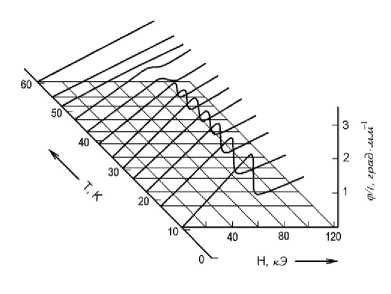
Рис. 5. Полевые зависимости кругового двупреломления света в Rb₂MnCl₄ от магнитного поля H || C₄ с λ = 632,8 нм при различных температурах

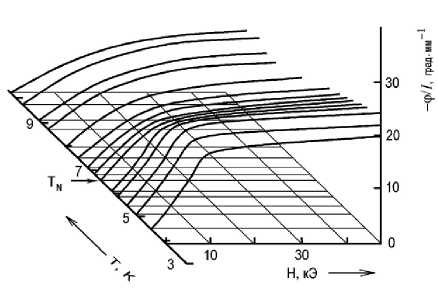
Рис. 6. Зависимости кругового двупреломления NaMnCl₃ от магнитного поля H || C ₃ с λ = 632,8 нм при различных температурах

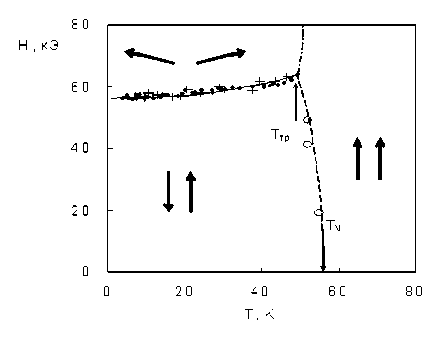
Рис. 7. Фазовая диаграмма Rb 2 MnCl 4 : поле H SF получено с помощью линейного (+) и кругового ( • и ○) двупреломления; линии графиков – схема ожидаемых фазовых границ

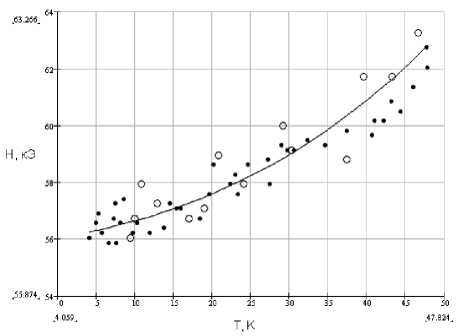
Рис. 8. Результат работы генетического алгоритма ( - ): поле спин-флоп перехода H SF получено с помощью линейного (○) и кругового ( • ) двупреломления

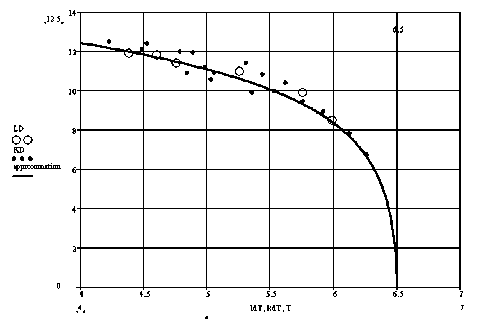
Рис. 9. Фазовая диаграмма NaMnCl3, построенная с помощью алгоритма генетического программирования и основанная на экспериментальных данных по измерению двупреломления света:

• – круговое двупреломления, H || C 3 ; ○ – линейное двупреломления, H ⊥ C 3

Таким образом, применение коэволюционного алгоритма генетического программирования позволило построить аналитические выражения для фазовых границ магнитного состояния кристаллов Rb 2 MnCl 4 и NaMnCl 3 , на основании которых можно сделать выводы о применимости предложенных модельных оценок.