Исследование колебаний композитного магнитоэлектроупругого биморфа в зависимости от объемных долей его компонентов на основе прикладной теории

Введение. Исследованы поперечные колебания биморфа, состоящего из двух пьезомагнитоэлектрических слоев и находящегося в переменном магнитном поле. Пьезомагнитоэлектрические слои представляют собой многослойный композит с чередующимися пьезоэлектрическими и пьезомагнитными слоями. Механические и физические свойства такого композита задаются известными эффективными константами.

Материалы и методы. Прикладная теория колебаний многослойной пластины учитывает нелинейное распределение электрического и магнитного потенциала в пьезоактивных слоях в продольном и поперечном направлениях. На основе указанной теории исследованы напряженно-деформированное состояние, зависимости прогиба, электрического и магнитного потенциалов от объемного соотношения состава шарнирно опертого биморфа. Электрический потенциал принят равным нулю на всех электродах, магнитный равен нулю на внутренней границе и неизвестен на внешних. Поэтому распределение электрического и магнитного потенциалов в середине слоя — неизвестные функции. В случае магнитного потенциала распределение на внешней границе также неизвестно. В задаче были приняты гипотезы Кирхгофа для механических характеристик. Использование вариационного принципа и квадратичной зависимости электрического и магнитного потенциалов по толщине пьезоактивных слоев позволило получить систему дифференциальных уравнений и граничных условий.

Результаты исследования . При изменении объемного соотношения состава пьезоактивных материалов биморфа электрический потенциал в середине слоя нелинейно изменяется. Магнитный потенциал в середине слоя и на внешней границе практически линейно увеличивается с увеличением объемного процента BaTiO 3 . Определена зависимость прогиба в середине слоя.

Обсуждение и заключения. Построена прикладная теория расчета поперечных колебаний биморфа с двумя пьезомагнитоэлектрическими слоями. Исследована зависимость характеристик напряженно-деформированного состояния, электрического и магнитного полей от объемных долей пьезомагнитного и пьезоэлектрического материалов.

Финансирование. Работа первого автора поддержана Правительством РФ (контракт № 075-15-2019-1928).

Третий автор выполнял работу в рамках ГЗ ЮНЦ РАН (№ госрег. проекта ААА-А-А16-116012610052-3).

Original article

Vibration analysis of a composite magnetoelectroelastic bimorph depending on the volume fractions of its components based on applied theory

Arkadiy N. Soloviev^1,2,    , Do Thanh Binh¹   , Valerii A. Chebanenko³   , Olga N. Lesnyak¹   ,

Evgeniya V. Kirillova⁴ ©

1Don State Technical University (Rostov-on-Don, Russian Federation)

2Southern Federal University (Rostov-on-Don, Russian Federation)

3Federal Research Centre the Southern Scientific Centre of the Russian Academy of Sciences (Rostov-on-Don, Russian Federation)

4Rhein-Main University of Applied Sciences (Wiesbaden, Germany)

Introduction. Transverse vibrations of a bimorph consisting of two piezomagnetoelectric layers and located in the alternating magnetic field are investigated. Piezomagnetoelectric layers are multilayer composites with alternating piezoelectric and piezomagnetic layers. The mechanical and physical properties of such a composite are given by known effective constants.

Materials and Methods. The applied theory of multilayer plate vibrations takes into account the nonlinear distribution of electric and magnetic potential in piezoactive layers in the longitudinal and transverse directions. On the basis of this theory, the stress-strain state, the dependences of deflection, electric and magnetic potentials on the volume ratio of the composition of the hinged bimorph, are investigated. The electric potential is assumed to be zero at all electrodes, while the magnetic potential is zero at the inner boundary and unknown at the outer boundaries. Therefore, the distribution of electric and magnetic potentials in the middle of the layer are unknown functions. In the case of the magnetic potential, the distribution at the outer boundary is also unknown. In the problem, the Kirchhoff hypotheses for mechanical characteristics were accepted. The use of the variational principle and the quadratic dependence of the electric and magnetic potentials on the thickness of piezoactive layers made it possible to obtain a system of differential equations and boundary conditions.

Results. When the volume ratio of the composition of piezoactive bimorph materials changes, the electric potential in the middle of the layer changes nonlinearly. The magnetic potential in the middle of the layer and at the outer boundary increases almost linearly with an increase in the volume percentage of BaTiO 3 . The dependence of the deflection in the middle of the layer is determined.

Discussion and Conclusions. An applied theory for calculating transverse vibrations of a bimorph with two piezomagnetoelectric layers is constructed. The dependence of the characteristics of the stress-strain state, electric and magnetic fields on the volume fractions of piezomagnetic and piezoelectric materials, is investigated.

Funding information: The work (first author) was supported by the Government of the Russian Federation (contract No. 075-15-2019-1928). The third author carried out work within the framework of the State Assignment of the Southern Scientific Center of the Russian Academy of Sciences (State Reg. Project AAA-A-A16-116012610052-3).

Механика

Введение. При производстве сенсорных и измерительных систем, малогабаритных бытовых приборов, сотовых телефонов и беспроводных сенсорных систем для мониторинга и диагностики технического состояния объектов не нужны мощные источники энергии. При этом обязательными условиями являются мобильность и энергонезависимость вышеперечисленных устройств.                                                          5

Пьезоэлектрические материалы напрямую преобразуют электрическую энергию в механическую и обратно. Это свойство позволяет широко использовать их в науке и технике. Данные материалы задействуют в ультразвуковых излучателях упругих и акустических волн, приемниках таких волн, устройствах подавления колебаний элементов машин и конструкций и т. п. В последнее время бурно развивается еще одна область применения пьезоэлектриков — устройства сбора и накопления энергии. В этом случае пьезоэлектрические материалы входят в состав пьезоэлектрических генераторов энергии (ПЭГ). ПЭГ помещаются на элементах машин или конструкций, которые интенсивно колеблются, находятся в зоне прохождения упругих волн или подвержены действию переменного давления. Основные типы этих устройств имеют биморфную или стековую многослойную структуру и испытывают изгибные или продольные деформации соответственно. На основе ПЭГ создаются маломощные источники электрического тока. В их числе — автономные источники питания (например, для устройств мониторинга повреждений в труднодоступных местах сооружений трубопроводов и т. п.). Обзор таких устройств есть в [1–2]. Один из способов конструировать эффективные ПЭГ — использование пьезоактивных композитов различного типа связности и неоднородных материалов на основе пьезокерамики, в том числе пористой.

Фиксировать или задействовать энергию переменного магнитного поля могут ПЭГ, в конструкции которых есть дополнительные электромагнитные элементы или постоянные магниты. Один из путей решения данной задачи — использование пьезомагнитных материалов в сочетании с пьезоэлектрическими. В этом случае переменное магнитное поле приводит к деформации пьезомагнетика и связанного пьезоэлектрика, в результате последний генерирует электрическую энергию. Существует класс материалов, обладающих пьезомагнитными свойствами. Пьезомагнетизм — это явление, наблюдаемое в некоторых антиферромагнитных и ферромагнитных кристаллах. Он характеризуется линейной связью между магнитной поляризацией системы и механической деформацией. В пьезомагнитном материале можно вызвать спонтанный магнитный момент, приложив механическое напряжение, или деформацию, приложив магнитное поле. В исследованиях пьезомагнитных материалов очень часто рассматривается CoFe 2 O 4 [3–5]. В [6–8] исследуется композит на основе CoFe 2 O 4 и BaTiO 3 , обладающий пьезоэлектрическими и пьезомагнитными свойствами одновременно.

Решения задач электроупругости и магнитоупругости приведены в [9–11]. В [12] развиты прикладные теории колебаний многослойных пьезоэлектрических пластин с учетом специфики распределения электрического потенциала по толщине конструкции.

Задачи об установившихся колебаниях электромагнитоупругого слоя и полупространства под действием гармонических нагрузок представлены в [13, 14]. Учтены предварительные напряжения, а также различные электрические и магнитные условия на границах. Исследовано влияние указанных факторов на дисперсионные свойства.

Ранее [15, 16] была разработана прикладная теория, которая учитывает неоднородное распределение электрического потенциала в продольном направлении и квадратичную зависимость по толщине. В этих же работах исследовано напряженно-деформированное и электрическое состояние шарнирно опертого и консольно закрепленного биморфа. В обоих случаях прикладная теория показала хорошую сходимость с результатами конечноэлементного моделирования. Авторы также получили прикладную теорию колебаний биморфа [17], состоящего из электроупругого и магнитоупругого слоя. Этот подход хорошо согласуется с результатами конечноэлементного анализа.

В данной работе рассматриваются колебания устройства в рамках плоской деформации. На основе вариационного принципа построена прикладная теория изгибных колебаний двухслойного пьезомагнитоэлектрического биморфа. Для установившихся колебаний получены граничные условия и система дифференциальных уравнений для четырех неизвестных функций (прогиб, электрический потенциал в середине слоя, магнитный потенциал в середине слоя и на внешней границе), зависящих от длины биморфа. Исследовано влияние разных процентных объемных соотношений состава биморфа на прогиб, электрический и магнитный потенциалы в определенных положениях. Результаты исследования позволяют выбрать состав композиционного пьезомагнитоэлектрического материала для достижения наиболее эффективной работы устройства.

Материалы и методы. Рассматривается пластина, состоящая из двух одинаковых пьезомагнитоэлектрических слоев. Она совершает установившиеся поперечные колебания в рамках плоской деформации. Каждый слой представляет собой композит 2–2 связности, состоящий из чередующихся пьезоэлектрических и пьезомагнитных слоев (рис. 1).

Рис. 1. Структура композита 2–2

В [8] найдены эффективные свойства такого композита. Большие поверхности слоев электродированы, а сами слои поляризованы по толщине. Биморф шарнирно закреплен по краям, все поверхности свободны от механических напряжений. На верхнюю и нижнюю границы пластины воздействует магнитный поток B ₀ , в то время как на границе между слоями магнитный потенциал считается равным нулю. Электрический потенциал равен нулю на всех электродах. Боковые поверхности считаются изолированными от магнитных и электрических полей.

Уравнения для описания колебаний композита с эффективными свойствами, связностью механических, электрических и магнитных полей, имеют вид [18]:

V-о + рf = pu,  V-D = °Q,  V-B = 0 , о = c : e - eT - E - hT - H, D = e : £ + к - E + a - H, B = h : e + aT - E + H - H, e = 1 (vu +(Vu)T), E = -Vф, H = -V^.                              (1)

Здесь σ и ε — тензоры механических напряжений и деформации, D и E — векторы электрической индукции и напряженности электрического поля, B и H — векторы магнитной индукции и напряженности магнитного поля, ρ — плотность материала, c — тензор упругих модулей, e — тензор пьезоэлектрических модулей, h — тензор пьезомагнитных модулей, κ — тензор диэлектрических проницаемостей, α — тензор магнитоэлектрических модулей, μ — тензор магнитных проницаемостей, f — вектор плотности массовых сил, σ — объемная плотность электрических зарядов, u — вектор перемещений, φ и ξ — электрический и магнитный потенциалы.

Граничные условия определяются для механического, электрического и магнитного поля соответственно.

Для первого случая отметим отсутствие механических напряжений на границе биморфа: ° j ■ j = 0,     i , j = 1,3 .

Биморф шарнирно закреплен на концах (рис. 2):

^ui 1(0,0) = ^ui l( L ,0) = 0, i = 1,3.

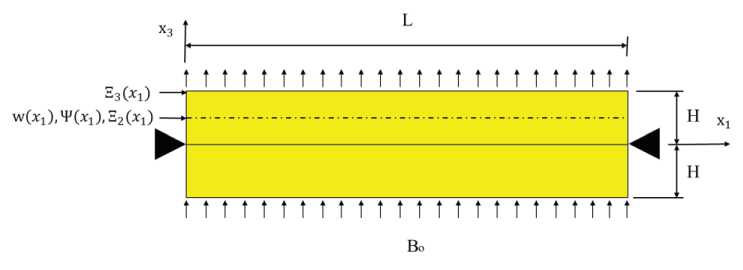
Рис. 2. Геометрия и граничные условия биморфа с композитными пьезомагнитоэлектрическими слоями

Механика

Далее сформулируем электрические граничные условия. Электрический потенциал на внутреннем и на внешнем электроде соответственно:

Укажем магнитные граничные условия. Магнитный потенциал на внутренней границе:

3 3 3 = 0 = ^M 0 .

Магнитный поток B₀ воздействует на верхнюю и нижнюю границы пластины: н\     = Д ) -

I x3 =± H

Воспользуемся вариационным уравнением для установившихся колебаний [10]. Оно обобщает принцип Гамильтона в теории электроупругости с учетом магнитных составляющих. Для случая плоской деформации при отсутствии поверхностных нагрузок и при наличии магнитного потока:

Ц 5HdS - р®2 JJ ui5 uidS + Ц (pi5 ui + a0 5ф + B0^) dS = 0,(2)

SSS где 5H = a 5s - D 5E - B 5H . ij ij            i i i i

Для построения прикладной теории колебаний примем гипотезы Кирхгофа. В соответствии с ними распределение перемещений по толщине имеет вид:

U 1 (3 1 , X ₃ ) = - Х ₃ W^ u 3 ⁽ Х 1 , Х₃) = w ^{( 3} 1 )                                         ⁽³⁾

В частности, для механического поля принята гипотеза единой нормали. Далее рассматривается задача, в которой значение электрического потенциала на электродах может быть равно нулю, поэтому его распределение не описывается линейной функцией. С учетом возможной неоднородности по длине элемента, связанной с влиянием граничных условий на концах биморфа, его распределение по толщине принимается квадратичным:

(       ² ^

ф( X 1 , X 3 ) = V ,( X , ) -3 1     - 1 1 + V ( X 1 ) | 1 - -2- | + V ( X 1 ) xL I     + 1 1 .                         (4)

H V н )      V H )       H V н )

Здесь X ₃ = - ₃ - H / 2 . Функции V ₀ , V 1 и У₂ отвечают за значение электрического потенциала на внутреннем электроде, в середине слоя и на внешнем электроде соответственно. Чтобы удовлетворить условиям задачи, примем эти функции в следующем виде (см. рис. 2):

V 0 ( - 1 ) = V) = const , V ( - 1 ) = ф ( - 1 ), V ₂( - 1 ) = V 2 = const -

Здесь функция Ф ( - 1 ) является неизвестной.

Представим квадратичное распределение магнитного потенциала по толщине каждого слоя.

Распределение по длине неоднородно, на внутренней границе слоев его значение принимается равным нулю: (      ² ^

«- 1 , - з ) = M 0 ( - 1 ) -3 1 -2 - 1 1+ M 1 ( - 1 ) | 1 -     | + M 2 ( - 1 ) -3 1 -¹ + 1 | .                     (5)

h V h )      V н )        н v н )

Здесь - ₃ = X ₃ - H / 2 . Функции M ₀ , M 1 и M ₂ отвечают за значение магнитного потенциала на внутренней границе, в середине слоя и на внешней границе соответственно и принимаются в следующем виде (рис. 2):

M ₀( - 1 ) = M 0 = const , M 1 ( - 1 ) = S ₂( - 1 ), M ₂( - 1 ) = 2 з ( - 1 ).

Здесь функции 5 ₂ ( - 1 ) и 5 ₃ ( - 1 ) являются неизвестными.

Соотношения (3)-(5) подставим в уравнение (2) и проинтегрируем его по толщине биморфа, а затем приравняем к нулю коэффициенты при независимых вариациях 5w, 5Ф , 552 и 553. Тем самым мы получаем систему из четырех дифференциальных уравнений (6) от четырех неизвестных функций, зависящих от -1 (далее опустим нижний индекс), и пять граничных условий (7).

Цзз. у + А^з з. v — 32.41 ф ( - ) - 32^ 31 5 ( - ) + 3 н ^  3 н  ^   3 H   ^v ’   3 н   ^v ’

16α

3 н

²¹5 з ( - )

16a, н d ² „ х х  2a, н d² „ , х  4 e.,H dx

--Т52( X)---75. ( X)--3

15 dx x ^2V ’    15    dx ^{2 3V} ’     3 dx -

16 ^21 у + 16^ 21 у — 32^ 31 ф ( - ) — 32^ 31 5 ( - ) + 16^ 31

3 H 0  3 H 2  3 н       3 н3

16a, H d ² „ , _х 2a, H d² „ , _х 4 h,H d^{2 11}75₂ ( X ) -    ¹¹₇5₃ ( X )³¹

15   dx2 2        15 dx2 3        3

—

—

—

16 , , H d²    , X

---¹¹--₇Ф( X )

15    dx -   ^V ’

/ х 16a. ,, w ( X ) +    3 ^{1 M} 0 = ⁰ ,

3 н

„ , , 16a, H d^г

5₃ ( X )¹¹

³         15 d-²

Ф ( X ) -

—

-

-

w ( x ) + ¹⁶^³³ M_n = 0, 3 H   ⁰

222 1 V

3 н ⁰

14α —

3 н

7- V ₂ +

16α

1 ^{1 ф (} - ) +

3 H

^5, (. X -)

3 H

—

14ц₃з - / 3 2a H dх    _х

¹¹5₃ ( X )--¹¹---ф( X ) -

ЗН ³      15   dx²

2ц_п H d²

15 d- -

5 h₃₁ H d^г

3   dx ²

w ^{( х} ) - 2 B 0 - - H. M 0 = ⁰,

4 eHd ²4 hHd ²5 hHd ²

—31-- ₇Ф( x ) + —31-- _?Е₂ ( x )--³¹---Е ( x ) - 2 p₃H -

3 dx ²3 dx ²²3 dx ²³³

2ρω ² H ³ d ²                    2 H ³ c d ⁴

-         2 w ( x ) + 2® p w(x ) H + —-— — w ( x ) = 0.

3 dx                        3 dx

16 H d

—¹¹-- Ф ( x ) +

15 dx

16 α ₁₁ H d

15 dx

2α Hd

( x ) +— ¹¹-- s₃( x ) = o,

16 α H d 16μ Hd 2μ Hd

----¹¹-- Ф ( x ) +     ¹¹-- s 2 ( x ) + -²-¹¹--S 3 ( x ) = 0,

15 dx         15 dx         15 dx

2 α H d 2μ Hd 4μ Hd

—¹¹-- Ф ( x ) + -²-¹¹-- s 2 ( x ) +    ¹¹-- S 3 ( x ) = 0,

15 dx         15 dx         15 dx e31HV

—

5 eH   4 eH

—31— V 2 + —³¹— Ф ( x ) +

4 h ₃₁ H

5 hH

⁽ x )--— - 3 < x ) +

2 H ³ c ₁₁ d ²

3 dx ²

w ( x ) + -31— M ₀ = 0,

—

4 e d 4 hHd

-^1 — Ф ( x )--³¹-- S 2 ( x ) +

3 dx         3 dx

5 h ₃₁ Hd

3 dx

( x ) - HAL dL

3 dx ³

2ρω ² H ³ d w ( x ) + -³—--- — w ( x ) = 0.

3 dx

Здесь были введены следующие обозначения:

^c 11 = c 11    ^c 13 / c 33 ,       ^e 31     e 31    c 13 e 33 / ^c 33 ,

^3i = h3i - Ci3h33 / c33,  a33 = -a33 - e33h33 / c33,  e33 = - 33 - e323 / c33. Они возникли после удовлетворения условию о33 = 0 и исключения £33.

Результаты исследования. Сопоставлены результаты расчета биморфа по предложенной теории с конечноэлементным расчетом в низкочастотной области для соотношения объемных долей пьезоэлектрического и пьезомагнитного компонентов 80 % BaTiO 3 и 20 % CoFe 2 O 4 . Сравнение показало, что погрешность в нахождении характеристик механического и магнитного полей менее 1 %. При определении электрического поля в средней части пластины разница составила порядка 5 %. Описывая ситуацию в окрестности точек опоры, следует отметить, что размер окрестности по продольной координате приблизительно равен толщине биморфа. Здесь при определении электрического поля зафиксирована разница 20 %.

Первым шагом исследования колебания двухслойного пьезомагнитоэлектрического биморфа при изменении объемного соотношения BaTiO 3 и CoFe 2 O 4 в составе композита является определение его эффективных свойств. В таблицах 1 и 2 представлены эти свойства, найденные по результатам работы [8].

Материальные константы (упругие модули, диэлектрические и магнитные проницаемости) для различной объемной доли BaTiO 3

Таблица 1

Объемная доля BaTiO 3 (%)	Упругие модули					Диэлектрические проницаемости		Магнитные проницаемости
	ГПа					10 – 9 Ф/м		10 – 4 Н с2/Кл2
	с 11	с 12	с 13	с 33	с 44	к 11	к 33	μ 11	μ 33
0	286,0	173,0	170,0	269,5	45,30	0,080	0,093	5,900	1,570
10	270,9	160,4	154,9	260,0	45,07	1,469	0,073	5,315	0,632
20	256,6	148,5	142,6	250,2	44,84	2,815	0,098	4,730	0,396
30	242,8	137,2	131,3	240,8	44,61	4,063	0,122	4,145	0,285
40	229,9	126,8	120,9	231,9	44,38	5,287	0,147	3,560	0,223
50	217,6	116,9	111,0	224,0	44,15	6,413	0,171	2,975	0,186
60	206,7	108,1	102,1	215,6	43,92	7,490	0,220	2,390	0,155
70	195,9	99,7	93,8	208,2	43,69	8,517	0,294	1,805	0,136
80	186,0	92,3	85,9	201,3	43,46	9,448	0,441	1,220	0,120
90	176,6	85,4	78,9	193,9	43,23	10,353	0,857	0,635	0,110
100	166,0	77,0	78,0	162,0	43,00	11,200	12,600	0,050	0,100

Механика

Таблица 2

Материальные константы (пьезоэлектрические, пьезомагнитные и магнитоэлектрические модули) для различной объемной доли BaTiO 3

Объемная доля BaTiO 3 (%)	Пьезоэлектрические модули			Пьезомагнитные модули			Магнитоэлектрические модули
	Кл/м2			Н/A м			10-8 Нс/ВКл	10-11 Нс/ВКл
	e 31	e 33	e 15	h 31	h 33	h 15	α 11	α 33
0	0	0	0	580,3	–699,7	550	0	0
10	–0,006	0,029	1,16	223,6	–244,1	495	–1,33	1,97
20	–0,013	0,059	2,32	130,0	–132,3	440	–2,35	2,36
30	–0,019	0,088	3,48	86,7	–79,8	385	–3,07	2,48
40	–0,025	0,132	4,64	61,6	–52,5	330	–3,48	2,50
50	–0,031	0,176	5,80	43,3	–34,2	275	–3,62	2,47
60	–0,038	0,220	6,96	29,7	–22,8	220	–3,45	2,43
70	–0,040	0,352	8,12	20,5	–13,7	165	–3,00	2,36
80	–0,060	0,571	9,28	13,7	–9,1	110	–2,27	2,29
90	–0,263	1,187	10,44	4,6	–4,6	55	–1,28	2,16
100	–4,400	18,600	11,60	0	0	0	0	0

Колебания биморфа возбуждались магнитным потоком, приложенным к верхней и нижней граням (рис. 2), который изменялся по гармоническому закону с амплитудой B 0 = 5 x 10 - 5 Вб и частотой 10 кГц.

На рис. 3 представлен прогиб в середине слоя в зависимости от объемной доли BaTiO 3 . Из графика видно, что прогиб в положении, имеющем координаты х 1 = L / 2, x 3 = H / 2 , равен нулю, если биморф состоит только из пьезоэлектрика BaTiO 3 . Прогиб биморфа достигает наибольшего значения, если в его составе только пьезомагнетик CoFe 2 O 4 . Прогиб практически линейно зависит от объемного соотношения составляющих пьезоактивных материалов.

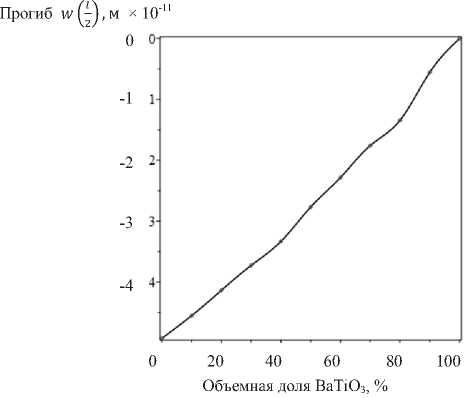
Рис. 3. Прогиб w (x 1 ) в середине слоя для различной объемной доли BaTiO 3

На основе данных рис. 4 можно сделать заключение, что электрический потенциал в середине слоя нелинейно изменяется при изменении объемного соотношения состава пьезоактивных материалов биморфа. Если биморф состоит только из BaTiO 3 либо CoFe 2 O 4 , то электрический потенциал в точке ( L /2, Н /2) равен нулю и достигает наибольшего значения при 35 % BaTiO 3 в составе биморфа.

Эклектический потенциал Ф

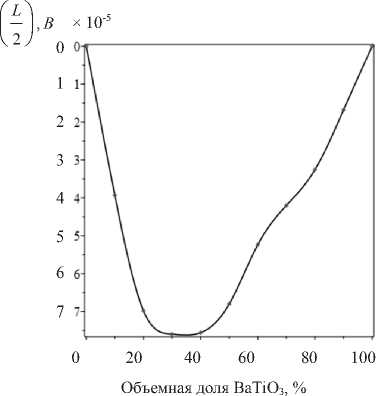
Рис. 4. Электрический потенциал Ф (х 1 ) для различной объемной доли BaTiO 3

Анализ рис. 5 и 6 позволяет сделать заключение, что магнитный потенциал в середине слоя S 2 ( L /2) и на внешней границе S 3 ( L / 2) практически линейно увеличивается с ростом объема BaTiO ₃ в составе биморфа.

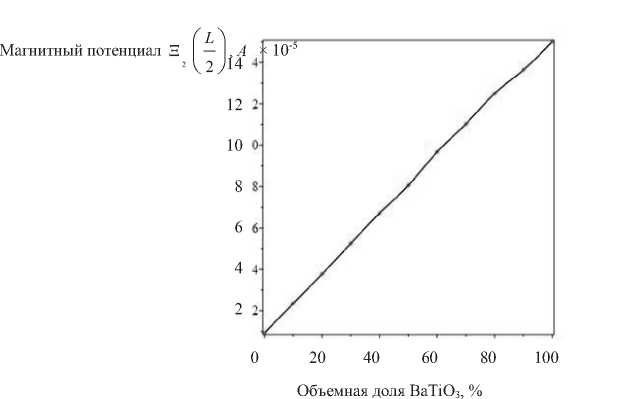
Рис. 5. Магнитный потенциал S ₂ ( L / 2) для различной объемной доли BaTiO 3

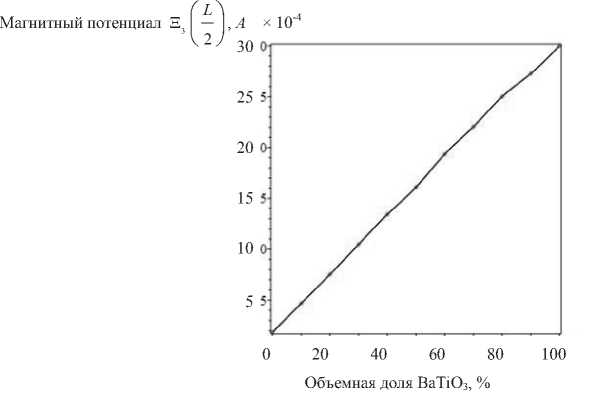
Рис. 6. Магнитный потенциал S 3 ( L / 2) для различной объемной доли BaTiO 3

Механика

Обсуждение и заключения. Предложена прикладная теория для расчета поперечных колебаний биморфа из двух слоев композита на основе CoFe2O4 и BaTiO3, обладающего одновременно пьезоэлектрическими и пьезомагнитными свойствами, в переменном магнитном поле. Такая конструкция может служить моделью пьезоэлектрического генератора устройства сбора и накопления энергии при действии внешнего магнитного поля. В низкочастотной области (ниже собственной частоты первой изгибной моды) проведены расчеты напряженно-деформированного состояния биморфа, распределения электрического и магнитного полей. Исследована зависимость прогиба, электрического и магнитного потенциалов от объемного соотношения состава биморфа. В дальнейшей работе предполагается определить выходной потенциал и мощность электрического тока, возбуждаемого переменным магнитным полем. Целью этих изысканий будет сбор электрической энергии.