Исследование компромиссного оптимума в MATLAB

Введение и задача исследования. Для электромеханических объектов второго-третьего порядков рекомендуется выбирать структуру и параметры регулятора по критериям модульного (МО) и симметричного (СО) оптимумов. Критерий МО обеспечивает плавные и быстрые переходные процессы по заданию и медленные по возмущению, критерий СО – быстрые по возмущению и затянутые, с перерегулированием до 54 %, по заданию. Для систем, регулятор которых выбран по критерию СО, рекомендуется включать на входе системы управления фильтр (апериодическое звено первого порядка) с постоянной времени 4Т μ , где Т μ – малая постоянная времени контура. Это позволяет снизить перерегулирование по заданию до 8–10 % [1–3].

Указанные недостатки критерия СО можно устранить, если ввести дополнительно встречнопараллельную коррекцию, которая обеспечит наилучшие динамические характеристики как по заданию, так и по возмущению, при малой чувствительности к вариациям параметров объекта управления. Такая задача называется синтезом регулятора по критерию компромиссного оптимума (КО) [3]. Решать её будем методами математического моделирования в MATLAB+Simulink [4].

Результаты исследования. Рассмотрим две системы управления. Первая (рис. 1) состоит из П-регулятора ( Wcmo) , структура и параметры которого выбраны по критерию МО и объекта управления (инерционное звено первого-второго порядка Wi с малой постоянной времени Т µ и интегрирующее звено Wm с большей постоянной времени Т 0 ) , на входе которого возможно появление возмущающих воздействий f

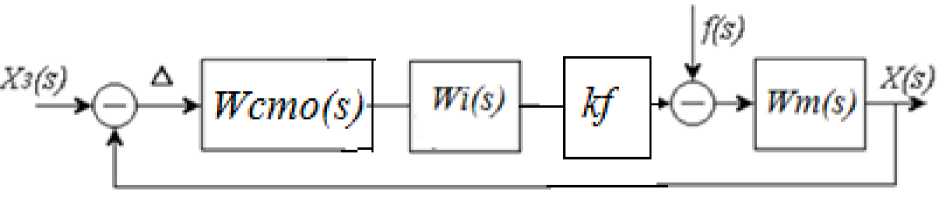
Рис. 1. Структурная схема системы управления

Вторая система (рис. 2) имеет регулятор Wсso , структура и параметры которого выбраны по критерию СО, объект и корректирующее устройство. Задача последнего – обеспечить переходный процесс по заданию в соответствии с критерием МО.

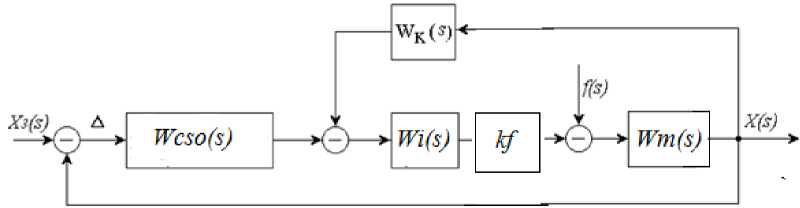
Рис. 2. Структурная схема системы управления с корректором

Для выполнения этого требования необходимо равенство передаточных функций разомкнутых систем по заданию (f = 0), представленных на рисунках 1 и 2

Wim(s)

1 + Wim(s) * Wk(s)

Wcmo(s) * Wim(s) = Wcso(s) *

где Wim(s) = Wi(s)*kf*Wm(s). Следовательно, передаточная функция корректирующего устройства Wk(s) =    1-- * ( ^Wcso(s^ - 1) .

Wim(s) Wccmo(s)

Будем считать, что

26.67                                  1

Wi(s) =                      ; kf = 1.36; Wm(s) =     , kds = 0.055;

0.0002s2 + 0.02s + 1                       1.3s

0.08s + 1

0.0049s .

Wcmo(s) = 16.2914; Wcso(s) =

Тогда передаточная функция корректирующего устройства

Wk(s) = 1.546e-008 s^A3 + 9.134e-005 s^A2 + 0.009057 s + 0.449.

Так как коэффициенты передаточной функции при s3 и s2 малы, принимаем, что

Wkk(s) » 0.009057s + 0.449 =0.449* (0.02s +1) = k(T_ps+1), где k =T o /(4Tpk p ); k p - коэффициент передачи разомкнутого контура при единичной обратной связи .

Такое корректирующее устройство технически легче реализовать.

На рисунках 3–6 представлены структурные схемы систем с регуляторами МО, СО, СО + корректор МО и системы с фильтром.

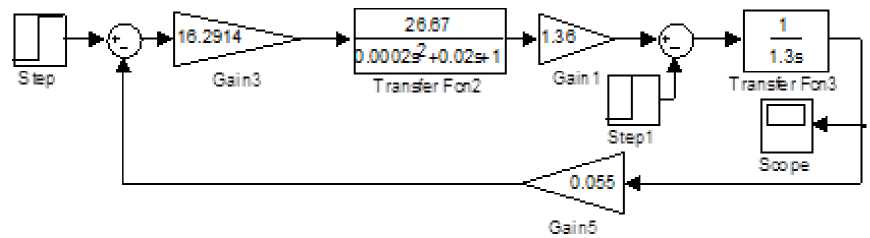
Рис. 3. Система с регулятором МО

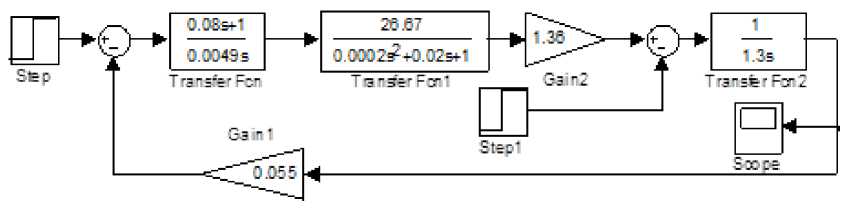
Рис. 4. Система с регулятором СО

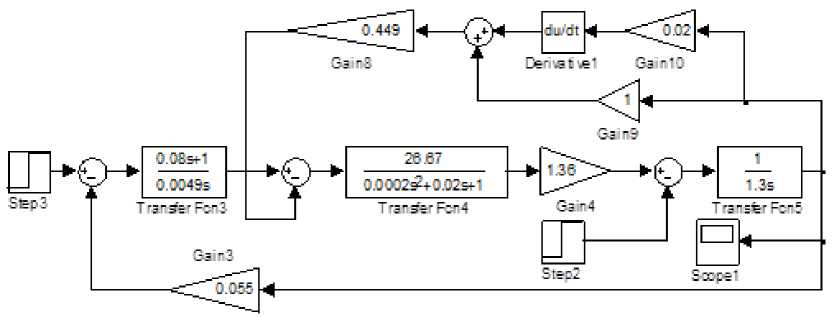
Рис. 5. Система с регулятором СО и корректором МО

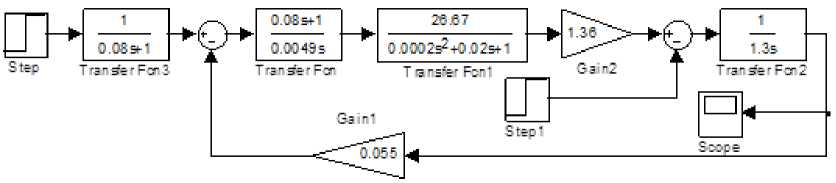
Рис. 6. Система с фильтром

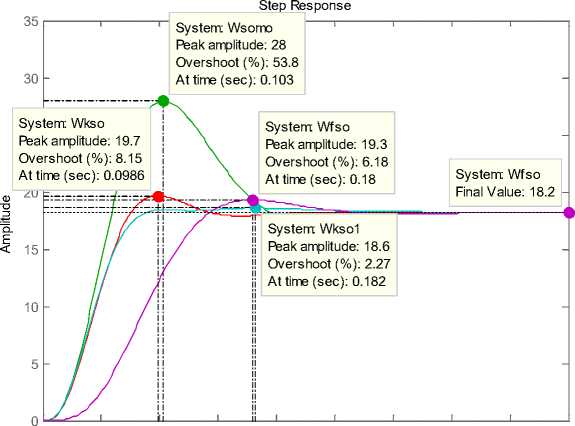
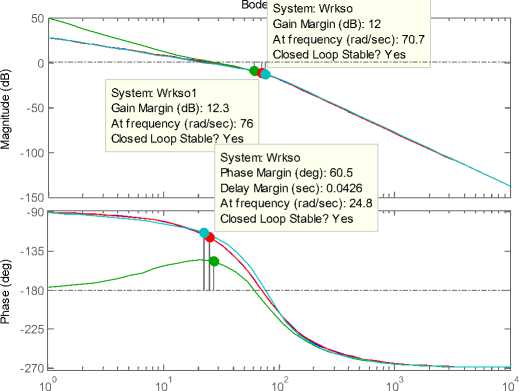
Прямые и частотные показатели качества систем управления оценим по переходным характеристикам (рис. 7) и диаграммам Боде (рис. 8). Результаты анализа представлены в таблице.

С помощью структурной схемы, представленной на рисунке 9, были получены переходные характеристики по возмущению f (рис. 10) для систем, регуляторы которых были синтезированы с помощью критерия МО (Wfmo), CO (Wfso) и СО+корректор МО (Wfkso). Результаты моделирования также представлены в таблице.

0      0.05      0.1      0.15      0.2      0.25      0.3      0.35      0.4      0.45

Time (sec)

Рис. 7. Переходные функции систем, настроенных по критерию МО (Wmomo),СО (Wsomo), с фильтром (Wfso,критерий СО), с корректором (Wkso, критерий СО, корректор МО) и корректором Wk(s) = 0.449(0.03s+1), Wkso1

Frequency (rad/sec)

Рис. 8. Диаграммы Боде систем управления

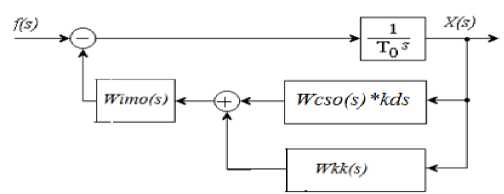
Рис. 9. Структурная схема системы по возмущению

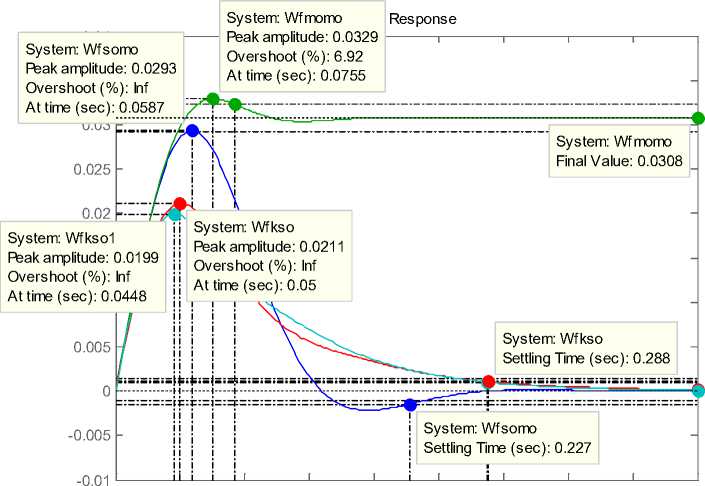
Рис. 10. Переходные функции систем управления по возмущению

0      0.05     0.1      0.15     0.2     0.25     0.3     0.35     0.4     0.45

Time (sec)

Прямые и частотные показатели качества систем управления по заданию

Система	По заданию				По возмущению
	t p ,c	σ, %	ΔL, д.б.	Δφ, град	t pf , c	σ f , %	ε
МО-МО	0,119	8,15	12	60,5	0,092	0,0329	0,0308
СО-МО	0,182	53,8	9,52	32,7	0,227	0,0293	0
СО-МО с Ф	0,202	6,18	-	-	-	-	-
СО-МО+К	0,119	8,5	12	60,5	0,288	0,0211	0
Wk(s) =0.449(0.03s+1)	0.076	2.27	12.3	65.9	0,288	0,0191	0

Выводы. Все системы имеют нулевую статическую ошибку по заданию, но лучшими по прямым и частотным показателям качества являются системы с корректирующим устройством – параллельным соединением пропорционального и дифференцирующего звена.

Если система с регулятором МО является статической по возмущению, то другие системы астатические. Переходная характеристика по возмущению систем с корректором без колебаний, что важно для электромеханических объектов, хотя длительность переходного процесса возрастает.

Оптимальные статические и динамические свойства, как по заданию, так и по возмущению, в условиях задачи имеет система с корректором, постоянная времени которого находится в диапазоне (1,3–1, 5) Т μ .

Рассмотренная коррекция равноценна введению ПИД-регулятора в контур скорости, система обладает большей устойчивостью по сравнению с нескорректированной. Тем самым обеспечивается меньшая чувствительность динамики контура к изменению параметров Т 0 , Т µ и коэффициента передачи разомкнутого контура [3].

Листинги программ в MATLAB приведены в приложении.