Исследование конвективной сушки натуральных кож методом комплексных переменных

Витебский государственный технологический университет

Сушка – процесс тепломассообмена, протекающий как непосредственно в самом материале, так и вблизи его поверхности.

Закономерности тепломассопереноса в материале оказываются в такой сложной взаимосвязи, что получение аналитических зависимостей из решений дифференциальных уравнений переноса представляет большие трудности. Поэтому важной задачей для практики сушки является определение продолжительности процесса сушки и температуры материала, так как качество готовой продукции, расход тепла на сушку, способ энергоподвода, размеры сушильной камеры существенно зависят от времени протекания процесса обезвоживания и длительности воздействия температуры на материал.

Сушка натуральной кожи – сложный комплексный теплотехнологический процесс, в котором кожа приобретает окончательные промышленные свойства и где параметры сушки являются основными определяющими факторами.

Основным препятствием для быстрой интенсивной сушки натуральных кож является значительная усадка при повышенных температурных режимах сушки. Поэтому сушка натуральных кож проводится при мягких температурных режимах теплоносителя t_ñ = 30–60 °C , скорости υ = 0,5–2 ì/ñ и высоких влагосодержаниях воздуха φ = 30–60 %.

Для расчета кинетики сушки представляют интерес приближенные, достаточно надежные экспериментальные уравнения с минимальным количеством постоянных, определяемых опытным путем. Причем наибольший интерес представляют такие методы, которые основаны на наиболее общих закономерностях процесса сушки и комплексных обобщенных переменных. ПОСТАНОВКА ЗАДАЧИ

Известно несколько приближенных методов расчета кинетики сушки [1]. Рассмотрим метод расчета кинетики сушки, основанный на обработке и анализе большого числа экспериментов по сушке различных материалов с разными способами энергоподвода [1–7]. Исследование конвективной сушки комплексными переменными позволило разработать новый метод расчета кинетики тепломассообмена в процессах сушки натуральных кож.

ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

На рисунке 1 представлены типичные кривые сушки u = f( τ ) и температурные кривые t = f( τ ) для процессов сушки юфти растительного метода дубления. Видно, что при мягких режимах сушки наблюдаются период постоянной скорости сушки с периодами постоянной температуры на уровне температуры мокрого термометра t_ì до критического влагосодержания u êð .

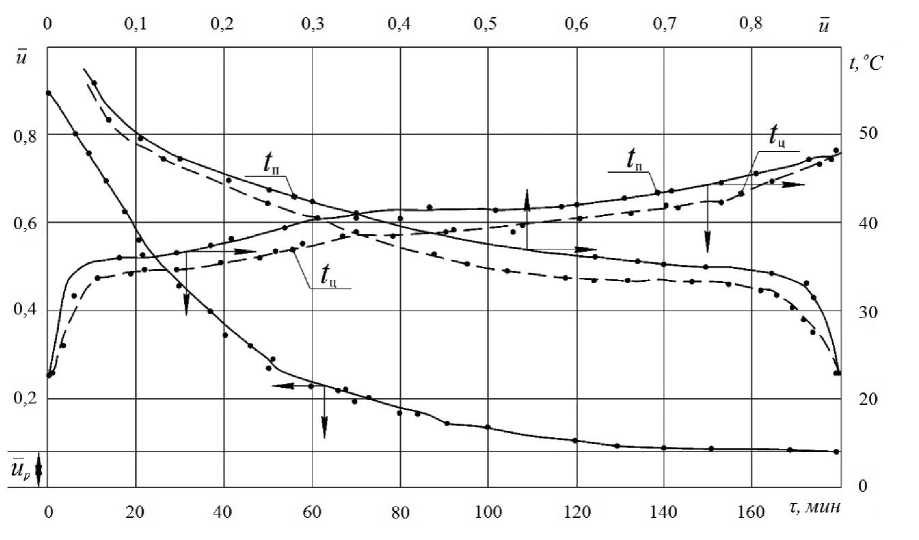
Рисунок 1 – Кривая сушки u = f( τ ) и температурные кривые для поверхности и в центре t_ï = f( τ ) ; t_ц = f( τ ) и t_ï = f( u ) ; t_ц = f( u ) для процессов сушки юфти растительного метода дубления при режиме сушки: t_ñ = 5 ^ï 0 °C ; υ = 0 ^ц ,5 ì/ñ ; φ = 40 %

Обработка многих опытных данных [4, 8] показала, что с достаточной точностью плотность потока тепла в периоде убывающей скорости сушки изменяется во времени по экспоненциальному закону:

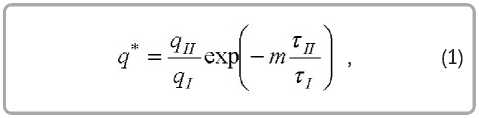
где q ^* ( τ ) – отношение потока тепла в периоде падающей скорости (второй период) q_II к потоку тепла в периоде постоянной скорости (первый период) q_I ; τ _II/ τ _I – отношение времени сушки в этих периодах.

Связь между обобщенными переменными τ _II/ τ _I и u / u êð устанавливается зависимостью, изображенной на рисунке 2. Зависимость аппроксимируется линейным уравнением

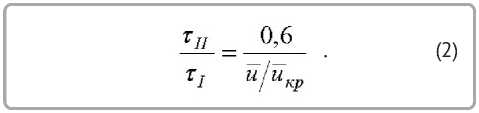
Плотность потока тепла в периоде постоянной скорости сушки определяется по формуле [1, 2]

Qi = rp^RyN , Âò/ì² ,    (3)

где r – теплота парообразования, ρ ₀ – плотность сухого материала, R_V = V/F = δ – толщина материала, определяемая как отношение объема тела к площади его поверхности, N – скорость сушки в первом периоде.

Плотность потока тепла в периоде убывающей скорости сушки

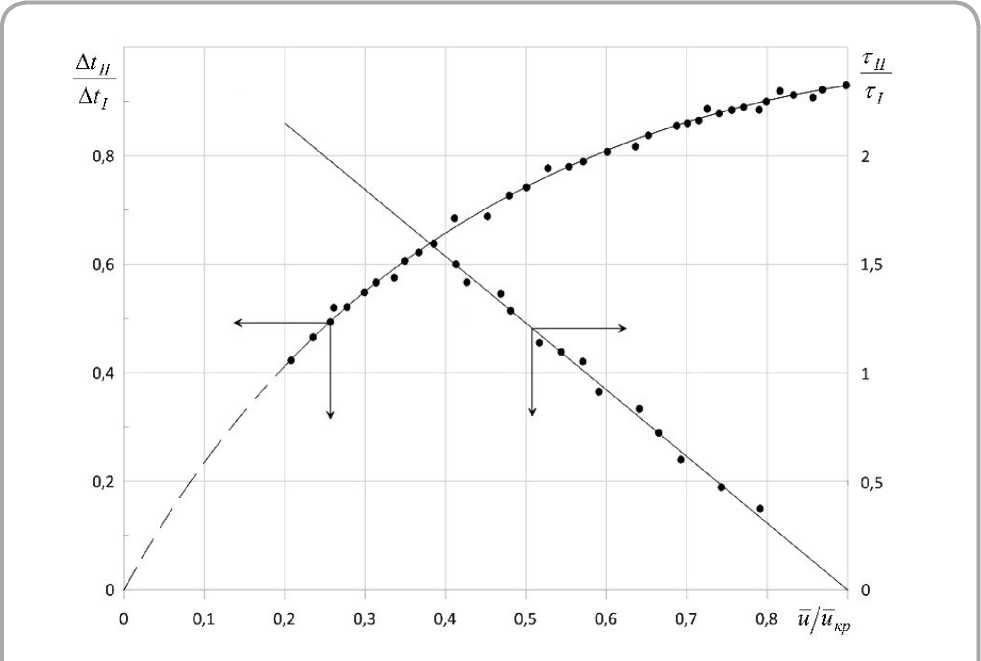
Рисунок 2 – Зависимости Δτ _II/ Δτ _I и τ _II/ τ _I от относительного влагосодержания u / u êð для процессов сушки юфти растительного метода дубления в диапазоне режимов сушки t_ñ = 40–60 °C ; υ = 0,5–2 ì/ñ ; φ = 30–60 %

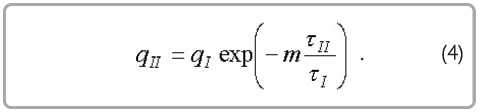
отношения влагосодержаний u ₀/ u _êð , для всех видов натуральных кож не зависит от режима сушки, и определяется уравнением

Интенсивность испарения влаги с поверхности влажного тела в первом периоде сушки m = 0,42^- . ^•кр

^₌^>^_{= O}D_N . (5)

Интенсивность испарения влаги во втором периоде сушки —

На рисунке 3 представлена зависимость постоянной m = f( u ₀/ u _êð) для различных натуральных кож в диапазоне изменения режимов сушки: t_ñ = 40–60 °C , υ = 0,5–2 ì/ñ , φ = 30–60 % .

Скорость сушки во втором периоде из (9)

x.

Qn                      I 77 I             I         77

Jn =--= PoRyN exp -m— = j, exp - m —

.

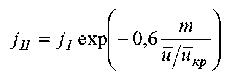
TII

У

dU

СШ XT          ^Tli

— = jvexp -m—— .

dr

Основное уравнение кинетики сушки, устанавливающее взаимосвязь между теплообменом q ^* и влагообменом N ^* [1, 6] имеет вид

Интегрирование уравнения (11) дает [5]

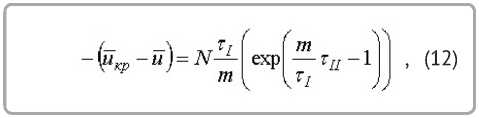
где N – скорость сушки в первом периоде, u – текущее влагосодержание материала.

После преобразований получаем длительность сушки во втором периоде [5]

.

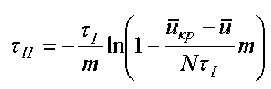
где Rb – число Ребиндера, устанавливающее связь между теплообменом и влагообменом при сушке. При мягких режимах сушки натуральной кожи число Ребиндера принимает максимальные значения при u →u_ðRb ≈ 0,15 [9] и этими значениями можно пренебречь.

Если пренебречь числом Rb при малых его значениях, получаем

Время сушки в первом периоде:

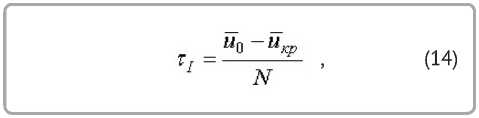
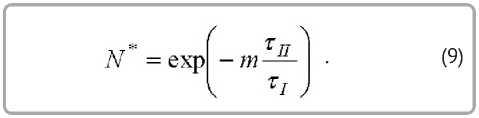
Постоянная m является линейной функцией

где u₀ и u_êð – начальное и критическое влагосо-держание материала.

Продолжительность сушки до любого заданного значения текущего влагосодержания равна [5]

,  _ ^ИО ^г1кр

11 ” N-

1- — In 1 m

икр

-и

u0 - и

— m

?кр

. (15)

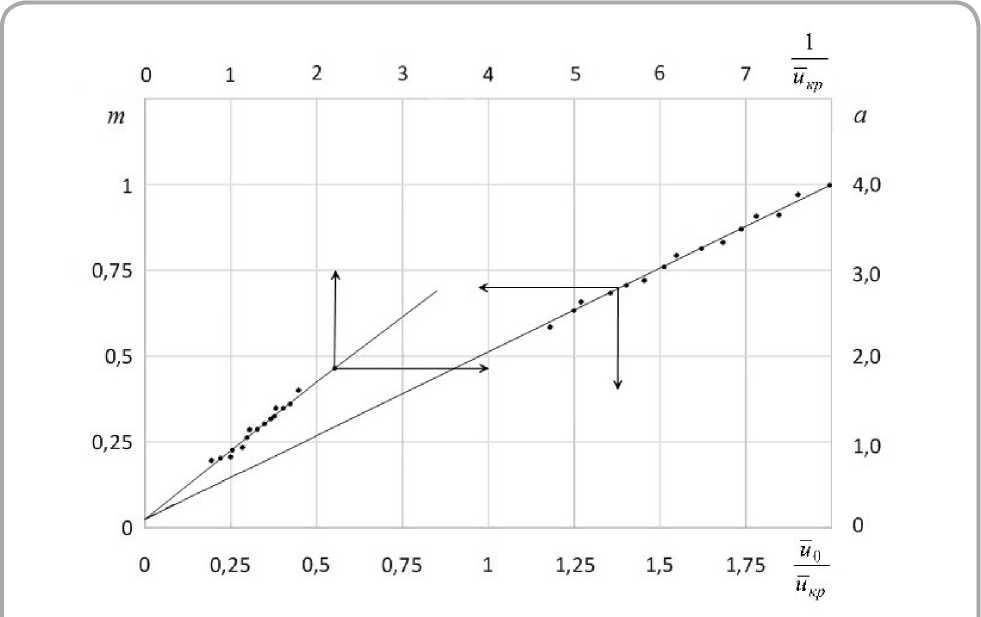
Рисунок 3 – Зависимости постоянной m от отношения влагосодержаний u ₀/ u _êð и коэффициента a от отношения 1/ u _êð для режимов сушки различных видов кож: t_ñ = 40–60 °C , υ = 0,5–2 ì/ñ , φ = 30–60 %

Рассмотрим метод, основанный на использовании относительной скорости сушки N ^* и обобщенного времени N _τ [6]. Величина N ^* не зависит от режима сушки и для конкретного материала будет функцией только влагосодержания u . Это положение является следствием, вытекающим из метода обобщения кривых сушки [1, 2, 4, 6]. Устойчивая комплексная переменная N _τ , характерная для сушки, позволяет перейти от единичного конкретного режима к множеству других режимов сушки [4], что значительно сокращает число экспериментов и уменьшает объем расчетной работы.

Из метода обобщения кривых сушки следует, что обобщенное время N _τ , как и относительная скорость сушки N ^* , является функцией влагосо-держания u и можно записать: N ^* = f( u ) , N _τ = = f( u ) и, следовательно, N ^* = f(N _τ ) [6].

Поскольку относительная скорость сушки N ^* изменяется от влагосодержания по экспоненциальной зависимости, то целесообразно проводить обработку эксперимента для зависимости

N ^* = f(N _τ ) в виде уравнения

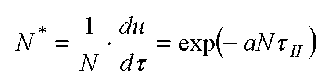
, где a – постоянная, определяемая опытным путем. Можно записать

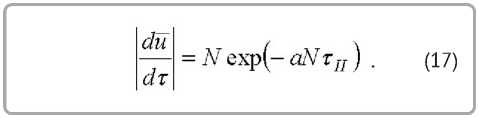
Интегрирование (17) дает длительность сушки во втором периоде [6]

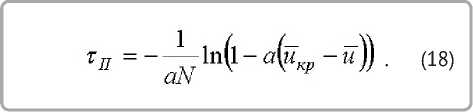
С учетом времени сушки в первом периоде имеем [6]

где коэффициент сушки K равен

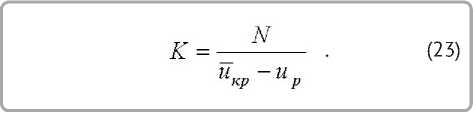
Основное уравнение кинетики сушки (7) можно записать в виде [1]

изменяется по экспоненциальной зависимости и скорость нагревания влажного тела dt/d τ можно приближенно представить в виде уравнения [10]

,

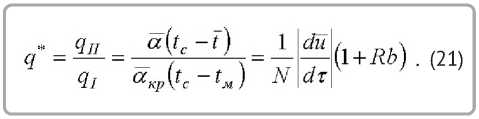
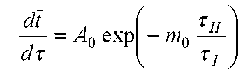
Скорость сушки:

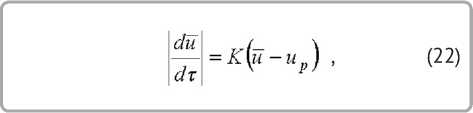
где отношение τ _II/ τ _I является обобщенной переменной сушки. Для постоянной A₀ при конвективной сушке натуральных кож обработкой данных получено соотношение [10]

Отношение, характеризующее уменьшение коэффициента теплообмена α во втором периоде сушки [1–6], определяется соотношением

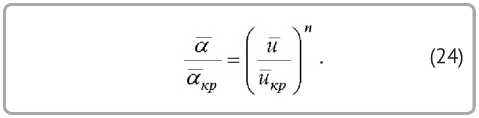
Пренебрегая числом Rb при малых его значениях и принимая в пределах допустимой погрешности u_ð→ 0, получим

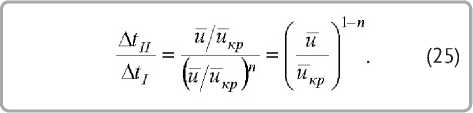
Обработкой опытных данных по сушке различных натуральных кож получено значение по-

Ло = 10 3 exp (О, If с) .       (28)

Скорость нагревания тела d t /d τ определяется графическим дифференцированием температурной кривой t = f( τ ) [1].

Значение постоянной m₀ в (27) совпадает со значением m в (1) и определяется формулой (10).

Запишем уравнение (27) в следующем виде:

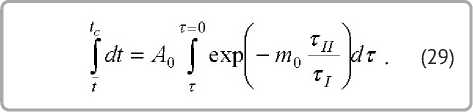
Интегрируя (29), получим выражение для среднеобъемной температуры материала для второго периода сушки [10]

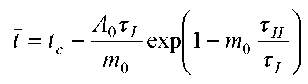
. (30)

Подставляя время сушки в первом периоде (14), получим

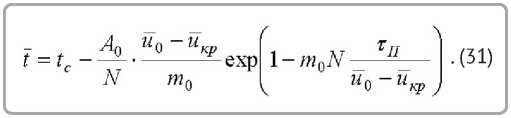
Время сушки во втором периоде можно с достаточной точностью определить, применяя линейную аппроксимацию для зависимости [1]

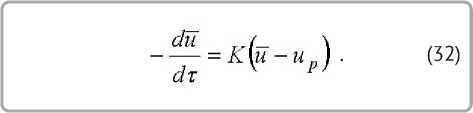
Интегрируя от u_êð до u и τ от 0 до τ _II уравнение (32), получим

.

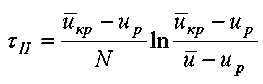
Между комплексными переменными Δ t_II/ Δ t_I и u / u _êð должна существовать нелинейная связь, поскольку и кривая сушки и температурная кривая представляют собой экспоненты.

Обработкой экспериментов при сушке юфти растительного метода дубления получена зависимость, представленная на рисунке 4, которая описывается уравнением [9] без учета равно- весного влагосодержания uð

.

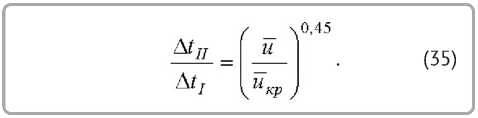
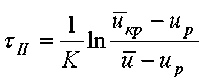
Среднеинтегральная температура в периоде падающей скорости сушки определяется выражением

С учетом (23) уравнение (33) принимает вид t =tc- (tc -tM\

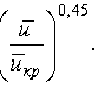
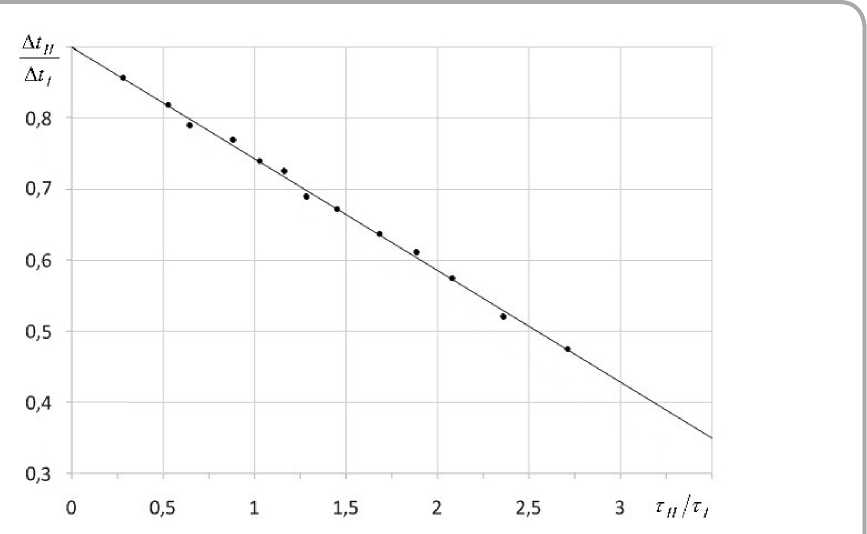
Рисунок 4 – Зависимость Δ t_II/ Δ t_I от отношения t_II/t_I для конвективной сушки юфти растительного метода дубления и рантовой подошвы в границах режимов сушки: t_ñ = 40–60 °C ; υ = 0,5–2 ì/ñ ; φ = 30–60

Связь между переменными A t II / A t I и t II /tI- , как показала обработка данных по сушке юфти растительного метода дубления и рантовой подошвы, оказалась линейной (рисунок 4) и описывается приближенным уравнением

.          (37)

Температура во втором периоде сушки равна

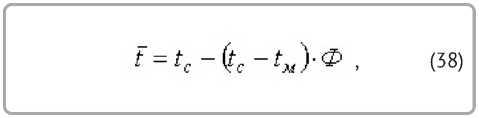
где

.          (39)

^7

В таблице 1 приведено сопоставление расчетных значений параметров кинетики сушки с экспериментальными и проверка достоверности полученных опытным путем уравнений. Видно, что разброс значений находится в пределах допустимой погрешности эксперимента. ЗАКЛЮЧЕНИЕ

Обработкой опытных данных по конвективной сушке натуральных кож обобщенными комплексными переменными получены приближенные, достаточно надежные экспериментальные уравнения для расчета основных параметров кинетики сушки.

Таблица 1 – Сопоставление экспериментальных значений с расчетными, полученными по формулам для процесса сушки юфти растительного метода дубления

Юфть растительного метода дубления; пластина 200*150x2,1 мм ; р ₀ = 560 кг/м ³ . Режим сушки: t_c = 50 °C ; и = 0,5 м/с ; ф = 40 % ; и₀ = 0,97; и_кр = 0,63; и_р = 0,12; N = 0,0048 мин ' .

и	т , мин экс.	т , мин (15)	т , мин (19)	t , °C экс.	t; °c (26)	t , °C (31)	t ; °c (38)	q , Вт/м 2 (1)
0,7	70	73	73	34,0	34,0	34,0	34,0	236
0,5	98	98	101	35,5	35,6	35,8	36,2	165
0,4	132	133	129	37,0	37,0	37,5	37,2	139
0,3	160	164	162	38,5	38,5	38,5	38,6	110
0,2	220	225	216	41,5	41,5	42,3	41,0	75

Москва, 286 с.

in the technology of leather and shoes], Moscow, 272 p.