Исследование конвективной теплопередачи в аппарате с механической мешалкой

Аппараты с мешалками широко используются в ряде отраслей промышленности при проведении различных технологических процес-сов[1-3]. Перемешивание в жидких средах оказывает влияние на теплообменные и массооб- менные процессы, а также на результаты химических процессов. Исследование теплообмена в аппаратах с мешалками представляет интерес как для выявления теоретических закономерностей, описывающих изменение температурного поля по объему аппарата, так и в связи с широким спектром технологического применения этих аппаратов. В настоящей работе проведено численное моделирование конвективного теплообмена в аппарате с лопастной мешалкой в условиях ламинарного режима течения вязкой жидкости.

Исходными уравнениями, описывающими неизотермическое течение жидкости в аппарате, будут соответственно уравнения Навье-Стокса, энергии и неразрывности в виде [4]:

р--+ р(v • V)v = F - Vp + pV2 v

8 t, (1)

— + — •V T = a V ² T ,

5t(2)

V-v = 0.

Течение жидкости будем рассматривать в подвижной цилиндрической системе координат r , φ ,z, связанной с вращающейся мешалкой. Проекции вектора скорости обозначим соответственно u , v , w . Проекции объемной силы в подвижной системе координат содержат ускорение Кориолиса и центробежное ускорение, а также ускорение силы тяжести и имеют вид:

F = p(m2 r + 2m v)F = -2pm u,

Fz = -pg, где ω – угловая скорость вращения вала и мешалки.

Свободную поверхность жидкости будем предполагать поверхностью вращения, на которой введем в рассмотрение локальный базис из вектора нормали

—► n =

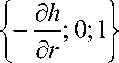
и двух векторов в касательной плоскости

—   /1    dh I   —

^T 1 = 1 1; 0; — ^ ,   ^T 2 = { 0; 1;

I     dr J где h – высота свободной поверхности жидкости над мешалкой.

Граничные условия на свободной поверхности включают в себя кинематическое и динамическое условия. Кинематическое условие ah     ah

— = - u+ w at      ar

свидетельствует о том, что скорость движения свободной поверхности в направлении нормали должна совпадать с нормальной составляющей скорости движения жидкости [5]. Динамическое условие представляет собой условие баланса сил, действующих на поверхности жидкости [6]. Можно предполагать, что силы поверхностного натяжения незначительны, так как радиус кривизны поверхности жидкости в аппарате достаточно велик. Тогда динамическое условие будет иметь вид n • P = — p^ • E,

, *                 *      ^r        *

t = пnt, r = —, ф ф , d где P - тензор напряжений; E - единичный тензор; pо - атмосферное давление.

Проекции динамического условия (5) на направления базисных векторов представляют соотношения

= s

z

d z — H — b

d h

Pzz + P 0 — 2 P- -  + (Prr d r

= 0,

— *

v

I h

— *

v

—7 ’ P nnd

при z <  H + b , при z >  H + b

P — P 0    _{0 =} T — T

p ( n nd ) ²        T 1 — T ₀

(Pzz — Prr     + оr

1  P h )²

1 — I I

<5 r )

P z = ⁰

dh

^P „ ^{— P}„ "r = 0,

где P r_r , P zz , P rz , p ,- , P r_v - компоненты тензора напряжений.

Граничные условия для составляющих скорости на твердых стенках заключаются в отсутствии относительного движения жидкости и твердой поверхности. Тогда на дне и боковой стенке аппарата

где n - число оборотов мешалки в единицу времени; H - высота расположения мешалки над дном аппарата; b - высота лопасти, а в качестве характерной длины и характерной скорости потока выбраны соответственно диаметр мешалки d и окружная скорость конца лопасти п nd . Свободной поверхности жидкости при этом будет соответствовать значение z ^*=1.

После преобразования координат уравнение неразрывности (3) сохранит форму

——

V- V = 0,

и = 0, v = —to r, w = 0,

в которой проекции вектора скорости в расчетной области U, V, W определяются как

а на поверхности вала и мешалки соответственно и = 0, v = 0, w = 0.

На оси вращения потока под мешалкой примем и = 0, v = 0,

d w d r

Будем предполагать процесс теплообмена в аппарате установившимся. Пусть цилиндрическая стенка аппарата оборудована наружными нагревательными элементами, поддерживающими постоянную температуру T 1 . Тогда на боковой стенке аппарата будет справедливо граничное условие T = T 1 . На свободной поверхности жидкости примем T = T ₀, где T ₀ - температура окружающей среды. На поверхности вала и мешалки, а также на дне аппарата примем адиабатическое условие д T /д n =0.

Поскольку форма свободной поверхности жидкости неизвестна и должна быть найдена в результате расчетов, то перейдем от физической области течения к расчетной области с известными границами. Для этого физическую область поделим на две подобласти, нижнюю и верхнюю, горизонтальным сечением, проведенным через верхнюю поверхность мешалки. Введем безразмерные координаты и функции

*                *                *       *  * ^д1

U = ^и , V = yv , W = w — и z —, dr где y=1 для нижней подобласти и y=h* для верхней подобласти; h = hId, а u , v , w - компоненты вектора скорости в безразмерной физической области, определяемой преобразованием

* r       *            * z r =-, Ф =Ф , z =-.

d              d

В расчетной области уравнение (1) в проекциях на оси координат может быть записано в виде обобщенного уравнения переноса

^7 + — div (V—ф)= div (Гgrad ф)+ 5, at    у                                     (9)

где Г=1/(пКс) - коэффициент диффузии; Re=p nd ²/p - центробежное число Рейнольдса; S -член типа источника, соответствующий искомой функции Ф. Уравнение (2) в безразмерной форме также приводится к виду (9), где r=1/(nRePr); Pr=p/(p a ); - число Прандтля; a - коэффициент температуропроводности.

Численное моделирование течения и теплопередачи проведем методом контрольных объемов [7]. Поделим расчетную область на контрольные объемы (ячейки) так, чтобы каждая узловая точка находилась в отдельной ячейке. Размещение всех узловых функций в одних и тех же точках приводит к рассогласованию полей скорости и давления, поэтому выберем разнесенную шахматную сетку [8], в которой точки, где вычисляются компоненты скорости, смещены на полшага в соответствующих направлениях относительно основных точек, в которых вычисляется давление. Проинтегрируем уравнение (9) по контрольному объему и временному интервалу At. В результате с учетом уравнения неразрывности получим дискретный разностный аналог, который связывает значения искомой функции Ф в узловой точке Р с ее значениями в центрах E, W, N, S, T, B соседних ячеек в форме

арФр = aE Ф e + aw Ф w + a Ф n + as Ф s +

(

+ a ,Ф, + a dOd + А V S_p

TT  BB    P

V

+Ф : 1

.

Здесь S P - узловое значение источникового члена; Ф⁰ - значение Ф в момент времени t * ; A V -объем ячейки.

Расчет поля течения проводился на основе алгоритма SIMPLE [7], в котором используется дискретизация уравнений по методу контрольных объемов на сетках с расположением узлов в шахматном порядке. Граничные условия на свободной поверхности (7), (8) и (4) использовались соответственно при расчете радиальной, тангенциальной и осевой компонент скорости из уравнений (10). Форма свободной поверхности жидкости, соответствующая рассчитанному полю течения, определялась из условия (6) с использованием кинематического условия (4) в конце каждой итерации. При этом в качестве начальных значений h i * ⁽⁰⁾ принималось значение, соответствующее положению невозмущенной поверхности жидкости. Очевидно, что рассчитанные при этом значения h i ** ⁽ k ) могут не удовлетворять условию постоянства объема жидкости в аппарате. Отметим, что достаточно учитывать объем жидкости над мешалкой. Таким образом, возникает необходимость введения некоторой поправки 5 h ^{( k} ) к величине h i ** ^{( k} ) . Эта поправка находилась из соотношения

V - V ^{( k )} =п ( R ² - r_s ² ) § h ^{( k )} ,

где R - радиус аппарата; rs - радиус вала; i - индекс нумерации узлов расчетной сетки в радиальном направлении; V0 - объем жидкости над мешалкой с невозмущенной свободной поверхностью; V(k) - объем жидкости над мешалкой на k-ой итерации, который вычислялся на каждой итерации путем численного интегрирования по значениям hi**(k). Следует отметить, что в соответствии с формулой (11) поправка 5h(k) не влияет на форму свободной поверхности, а лишь корректирует ее по высоте. Окончательно с учетом поправки 5h(k) скорректированные значения формы свободной поверхности могут быть найдены как h,' k) = h k) +5h(k).

Дискретные уравнения (10) решались методом прогонки в радиальном направлении. В качестве критерия сходимости рассматривалась сумма модулей невязок по всем ячейкам для уравнений (10). Расчеты проводились с точностью до 10-6. В расчетах принималось

H ₀ = D;  d / D = 0,5;   d_s / D = 0,05;

b / d = 0,2;   H / H _o = 0,3;

где D - диаметр аппарата; H 0 - высота невозмущенной поверхности жидкости над дном аппарата; d s - диаметр вала.

На рис. 1 представлены результаты расчетов в меридиональной плоскости аппарата линий тока радиально-осевой циркуляции. Мешалка создает потоки жидкости, которые вызывают циркуляцию жидкости по объему аппарата. Окружная циркуляция, называемая также первичной, связана с вращением массы жидкости вокруг оси вращения мешалки. Существенную роль в перемешивании играет вторичная радиально-осевая циркуляция, которая накладывается на основную окружную циркуляцию и связана с насосным действием мешалки. Наблюдается два потока радиально-осевой циркуляции, способствующих перемешиванию жидкости и расположенных соответственно сверху и снизу от мешалки.

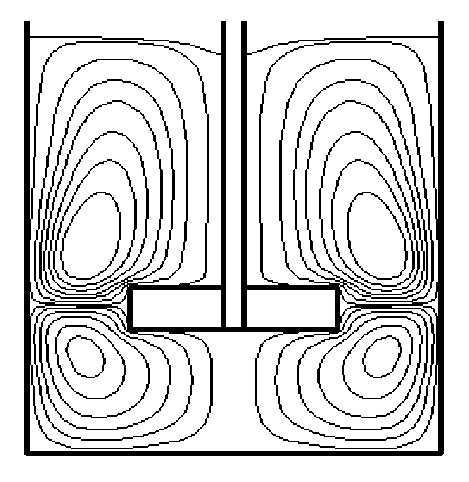
Рис. 1. Радиально-осевая циркуляция в аппарате при Re=150; Pr=2

На рис. 2-3 представлены результаты расчетов изотерм θ= const в горизонтальном сечении аппарата над мешалкой на расстоянии 0,15 H 0 . При относительно небольших значениях числа Рейнольдса конвективный перенос теплоты в направлении от боковой стенки в центральную часть аппарата незначителен и формирование температурного поля определяется в основном теплопроводностью (рис. 2).

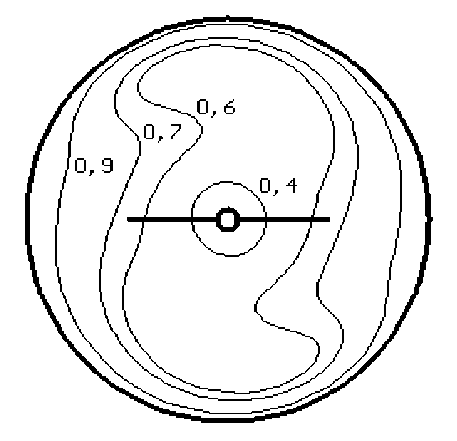
Рис. 2. Картина изотерм в аппарате при Re=50; Pr=2

Увеличение числа Рейнольдса сопровождается интенсификацией радиально-тангенциальных потоков. Роль конвекции в переносе теплоты возрастает. Особенно заметна тенденция к усилению конвективного переноса теплоты в тангенциальном направлении. Нагретые массы жидкости увлекаются быстро движущимися потоками, способствуя перемешиванию и постепенному выравниванию температур (рис. 3).

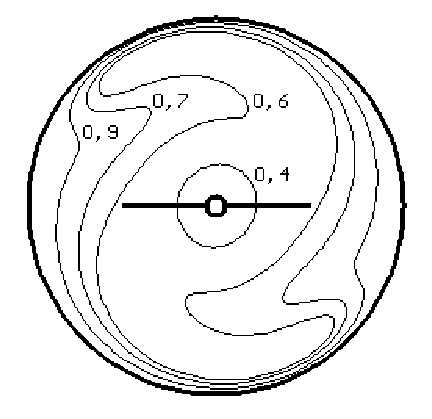
Рис. 3. Картина изотерм в аппарате при Re=200; Pr=2