Исследование корональных выбросов массы методом двухпозиционного радиозондирования

Существующие кинетические модели, которые описывают солнечный ветер в широком диапазоне изменения гелиоцентрического расстояния, строятся в приближении стационарного сферически симметричного потока квазинейтральной бестоковой полностью ионизованной плазмы и основываются на уравнениях для одно- и двухчастичных функций распределения (например, [5, 6]). Двухчастичные кинетические модели воспроизводят наблюдаемое ускорение солнечного ветра в плоскости эклиптики при учете только одного источника энергии – теплового движения частиц у основания солнечной короны, где истекающая плазма предполагается равновесной. Одночастичные (а также гидродинамические модели) дают при тех же допущениях значительно меньшие предельные скорости солнечного ветра (например, [8, 7]), что демонстрирует рисунок.

Рис . 1. Данные наблюдений по скорости солнечного ве тра [9] и теоретические зависимости , полученные в рамках одночастичной кинетической модели Лемера [8] ( штрих - пунктирная линия ) и двухчастичной кинетической модели [4] ( сплошная линия ), а также двухжидкостной гидродинамиче ской модели Хартля и Барнеса [7] ( пунктирная линия ).

В настоящей работе предпринимается попытка проанализировать основные допущения статистической механики, которые лежат в основе одно- и двухчастичных кинетических моделей и обусловливают достаточно существенное их различие при описании ускорения солнечного ветра.

Многочастичная статистическая модель

В рамках классической статистической механики макроскопические параметры (такие как плотность, скорость, температура и другие) определяются на основе одночастичной функции распределения f ₁( r , p , t ), описывающей вероятность f ₁ d p того, что частица с координатой r в момент времени t имеет импульс в интервале значений ( p , p + d p ). Рассмотрим в качестве примера выражение для числовой плотности:

• <    n ( r , t ) >= J f 1 ( r , p , t ) d p . (1)

Здесь интегрирование проводится по области определения функции f ₁ в пространстве импульсов, вид которой зависит от конкретной постановки задачи.

Определение плотности через одночастичную функцию распределения (1) является следствием задания микроскопической плотности в виде суммы функций Дирака, которые идентифицируют совпадение координаты наблюдения r с координатой r _i одной из N частиц рассматриваемой системы [10, 11]:

n ( ^{r ,} t ) = S и ⁸ ( ^r - ⁽ t ) - ^r ) . ⁽²⁾

Действительно, усреднив (2) на основе плотности распределения вероятности F ( r 1 , p 1 ,…, r N , p N , t ), описывающей систему N частиц, мы приходим к соотношению (1):

• <    n ( r , t ) >= J nFd r 1 d p_P .. d r _Nd p _N = J f , ( r , p , t ) d p . (3)

Здесь функция F интегрируется по области ее определения с учетом нормировки: ∫ Fd r 1 d p 1 … d r N d p N =1.

Заметим, что аддитивно-точечная форма задания микроскопической плотности (2) предполагает различимость координат всех частиц, т. е. базируется на основополагающей гипотезе классической статистической механики.

Однако измерения макроскопических параметров проводятся с конечными масштабами разрешения, в пределах которых координаты частиц неразличимы для наблюдателя. Учет этого обстоятельства в рамках классического подхода возможен путем осреднения макроскопических параметров по пробному объему $ , имеющему масштаб разрешения измерений (масштаб неразличимости). Такое осреднение приводит к суммированию вероятностей нахождения частиц в объеме $ , что можно проиллюстрировать на примере числовой плотности (3)

• ¹ 1 < n ( г , t ) >  d г = ¹ X M J f . ( r , Pp t ) d P. . V $ V

Здесь V - объем области $ , г - ее средняя координата, M - число частиц в этой области. Суммирование вероятностей характерно для взаимоисключающих событий, в то время как нахождение в пробном объеме частиц, не различимых по их координатам, характеризуется совместной вероятностью одновременных событий. Как следствие, расчет измеряемых макроскопических параметров системы частиц основывается на совместной функции распределения вероятностей f _м ( $ ⁾( г ₁,р₁,^, г _м, р _м ,t):

f M ( ^г 1 > P 1-- r M , P M , t ) = J ^ Fd r l d P 1- d r N d P N =

• = P ( N , M ) J Fd г m + i d p M + | ... d r N d P n . (4)

Определение (4) базируется на M-частичной микроскопической фазовой плотности vM” = X ,Л M1 ^,- r)5(p j- Pi), (5)

имеющей в отличие от (2) мультипликативный характер. Суммирование в (5) проводится по несовпадающим индексам j_i и обеспечивает все возможные перестановки из числа частиц всей системы ( N ) по числу координат r i '$' в объеме $ ( M ), которые порождают эквивалентные макросостояния системы. P ( N , M ) обозначает количество таких перестановок.

Выражение для vм($) (5) отличается от классического определения микроскопической фазовой плотности [10, 11] тем, что точки наблюдения с координатами <$' (i =1, ..., M) расположены компактно - в пробном объеме $. Соответственно, M-частичная функция распределения fM<$)(гl<$), рь...,гм($), pм, t) (4) описывает совместную вероятность для частиц с импульсами вблизи значений pi иметь координаты гi($), принадлежащие области $. При этом пробный объем $, имеющий масштаб разрешения измерений, исключается из области интегрирования функции F по координатам N-M частиц в соотношении (4), так как при вычислении вероятности нахождения M частиц в $ другие N-M частиц не могут попасть в этот объем. Классическая же частичная функция fM вычисляется путем интегрирования функции F по всему конфигурационному пространству, что обусловлено гипотезой о различимости координат частиц.

Отметим, что компактная микроскопическая фазовая плотность v _м ( $ ) может быть записана не через функции Дирака, а через соответствующие интервальные функции по переменным г i У Это позволит формализовать исключение пробного объема из области интегрирования в соотношении (4).

Интегрируя функцию f_M ( $ ) (4) по координатам частиц из объема $ ( г ) и их импульсам, получаем вероятность флуктуаций числа частиц в этом объеме:

Wm ( г , t ) = 1 P ( M , M ) J /м ) dг™ 1 d Р 1 >- d г М $ d p M . ⁽⁶⁾

Среднее значение числа частиц в объеме $ , или локальная числовая плотность, вычисляется тогда как среднее значение флуктуирующей величины:

• < M >= У " Mw„ (г , t ). (7) м = 0 ^M ' ’ / ⁷

Таким образом, видим, что при классическом определении локальных среднестатистических параметров среды, основанном на предположении о пространственной различимости составляющих ее частиц и, соответственно, на суммировании вероятностей каждой частицы находиться в заданном объеме, статистическое описание такой среды сводится к одночастичастичным кинетическим моделям. Гипотеза же о пространственной неразличимости частиц, обусловленной масштабом разрешения измерений, закладывает в основу определения локальных средних характеристик совместную вероятность нахождения M частиц в пробном объеме $ , т. е. M -частичные функции распределения f_M ( $ ) (4).

Гипотеза о детальном динамическом рав новесии

Для корректного применения многочастичного подхода важным является вопрос, который затрагивает основы любой кинетической модели. Как следует определять систему N частиц, для которой выполняется теорема Лиувилля и на основе которой строится цепочка приведенных M -частичных функций распределения ( M < N и соответствующих кинетических уравнений [10]? Обычно этот вопрос решается путем выделения изолированной системы, состоящей из постоянного числа частиц N («термостат»). Как можно выделить такую систему для случая солнечного ветра, частицы которого, вылетая с поверхности Солнца, движутся как по траекториям, имеющим возвратные точки (частицы атмосферы), так и по траекториям, уходящим на бесконечность (убегающие частицы)? Учитывая топологию фазового пространства, представляется логичным выделить в конфигурационном пространстве объем Е , содержащий N частиц и ограниченный поверхностью S , составленной из двух сфер (граничную поверхность можно взять произвольной формы; сферы выбраны для большей простоты изложения). В случае динамического равновесия рассматриваемой открытой системы, занимающей объем Е , с окружающей средой встречные потоки частиц, пересекающих граничную поверхность

Н . Р . Минькова

S взаимно компенсируются как по числу частиц, так и по переносимой ими энергии и моменту количества движения. Таким образом, законы сохранения в целом для всей рассматриваемой системы N частиц выполняются так же, как и для изолированной системы. При этом обмен энергией, моментом количества движения на границе S при динамическом равновесии ничем не отличается в фазовом пространстве импульсов от такого обмена между частицами при их столкновениях внутри объема Е . Изменение индивидуальности частиц при обмене через границу S не отражается на фазовом портрете динамически равновесной системы, если сохраняется число частиц системы (каждого сорта) и выполняются другие законы сохранения при каждом акте обмена (а не только в среднем за время равновесного обмена). Последнее условие можно назвать приближением детального динамического равновесия.

Предположим, что рассматриваемая открытая система находится в детальном динамическом равновесии с окружающей средой и, таким образом, обладает теми же свойствами в фазовом пространстве импульсов, что и изолированная система. Тогда для нее справедлива теорема Лиувилля, следствием которой является постоянство функции распределения F всей системы вдоль траекторий частиц системы:

F ( r 1 , p 1 ,..., r N , p N , t ) = const . (8)

Уравнение (8), дополненное граничными условиями на поверхности S , с которой выходят траектории частиц: F|_S = F ₀, позволяет найти функцию F во всем объеме, занимаемом системой.

В рамках рассматриваемого подхода частичная функция f_M ^№ находится из уравнений (4), (8). Такой выбор метода вычисления функций f_M ^№ обусловлен тем, что вывод кинетических уравнений для них представляется затруднительным, так как размерность этих уравнений M , равная числу частиц в пробном объеме ^ , зависит от координаты этого объема r и изменяется на порядки в потоке солнечного ветра.

Заметим, для стационарного потока выбор объема системы Е может быть произвольным, но число частиц в нем должно быть достаточным для обеспечения применимости статистического подхода.

Тестовые задачи

Для тестирования многочастичного статистического подхода рассмотрим две классические задачи. Применяя данный подход к решению задачи о флуктуациях плотности в ограниченном объеме, занятом однородным идеальным газом, приходим к известному решению – биноминальному распределению вероятности актуальных значений числа частиц в выделенном объеме (которое, как известно, в пределе при больших значениях числа частиц переходит в распределение Пуассона, а при относительно малых флуктуациях в распределение Максвелла) [12]. Для задачи об идеальном газе в гравитационном поле получаем также биноминальное распределение для флуктуаций числовой плотности с ее средним значением, совпадающим с классическим распределением Больцмана (барометрической формулой).

Стационарный солнечный ветер

Рассмотрим стационарный бесстолкновительный поток квзинейтральной двухкомпонентной (элек-трон-протонной) плазмы, сферически расширяющейся в гравитационном поле. Для частиц плазмы, истекающей со сферической поверхности радиуса r 0 , расположенной в короне Солнца, задается максвелловское распределение по скоростям. Взаимодействие между частицами учитывается только через среднее поле поляризации плазмы (столкновениями пренебрегается). Дебаевский радиус предполагается много меньшим масштаба разрешения измерений. Тогда функция распределения F для всех N частиц системы запишется как произведение функций распределения N e электронов f e и N р протонов f p :

^F = П N ^{f (} r ’ Р^ П ^N = 1 ^fP ( r j '’ P j ) .            ⁽⁹⁾

Из соотношений (4), (6), (9) получаем вероятность w m нахождения M частиц плазмы в объеме ^ :

Wm = П k=e, P

N ’ Nk

M k

( N k — M k ) ! M k !^. k ⁽ k )

I N k ^{- Mk} . (10)

Здесь учтено количество перестановок идентичных по свойствам частиц из объемов ^ и Е - ^ , дающих эквивалентные макросостояния. Индексы e, p относятся к электронам и протонам. Среднее значение (7) полиномиального распределения (10) П k= _e , _pN_k 0 _k ( 0 H fd r k d p k ) и допущение о квазинейтральности плазмы ( N_e=N _з =N /2) приводят к выражению для числовой плотности < n > как среднегеометрическому плотностей электронов n_e и протонов n_p :

< n >=

n e n p ^,

2 ^- Erf ч^{Ф ) -}^ e ^Ф k [ 1^- ^ ] ^-

n o -АФ, n = — e ^k k ₂

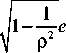
АФ k p ² - 1

[

^{2 -} Er*'

V

I — I

JД

V 1 +p^{- 1}

V

, k=e , p ,

где АФ k = Ф k -Ф k _ ₀, Ф k = ( m k ф + q k y )/( k B T₀) , m_k , q_k - масса и заряд частиц k -го сорта, ф - гравитационный потенциал Солнца, у - потенциал поляризации плазмы, k_B – постоянная Больцмана, T ₀ – температура частиц плазмы при r = r ₀, p = r/ r ₀ , Ф _k ,₀ = Ф _k ,₀ l _p= 1 .

Заметим, что выражение (11) представляет собой частный случай более общей формулы для числовой плотности квазинейтральной ( Е _kq_kn_k =0) полностью ионизованной K -компонентной плазмы, которая соответствует Q -частичной кинетической модели

< n >= П Lx n ^a k ’ ^а k = q k l/ Q ’ Q = S _k q k . ⁽¹²⁾

Размерность модели Q определяется набором минимальных значений K целых чисел l_k , удовлетворяющих условию S _k=1 q_kl_k = 0.

Плотность потока частиц Nu рассчитывается на основе многочастичного момента импульсов:

w N“ = M 1м 1 1 f M^' П, — ^d r d P - ’

^Nu   N_e ! N_p ! ^{M i} m_i^{i i}

где умножение (по индексу i ) проводится по всем частицам. В рамках принятых допущений приходим к полиномиальному распределению для флуктуаций потока частиц плазмы Nu со средним значением:

< Nu >= ^< Nu e ><  Nu p >  =

Nk BK e ^2 ^k B ^T 0 ^(1 -Ф e , ₀)(1 -Ф p ₀) -L.

T.J m e m p                             ^p

Зависимости (11) и (14), выведенные выше на основе многочастичного подхода, совпадают с выражениями для плотности и потока частиц, полученными на основе двухчастичной кинетической модели [4], и согласуются с данными наблюдений для солнечного ветра вблизи плоскости эклиптики (поляризационный потенциал ψ рассматривался в равновесном приближении). Расхождение теоретической зависимости для числовой плотности потока плазмы (14) с данными измерений не превышает 30 % [13, 14], а теоретическое значения скорости солнечного ветра < u >=< Nu >/< n >, рассчитанные по формулам (11), (14), лежат в пределах разброса наблюдательных данных [9, 14].

В отличие от одночастичных кинетических (и гидродинамических) моделей результаты, полученные в рамках многочастичного подхода, согласуются с данными наблюдений как по скорости, так и по плотности солнечного ветра при учете только энергии теплового движения частиц истекающей плазмы (без введения дополнительных источников энергии), что может служить аргументом в пользу последнего.

Заключение

Проведенный в работе анализ показал, что допущение о различимости координат частиц, принятое в классической механике, приводит к линеаризованной модели плазмы, которая базируется на одночастичных функциях распределения. При этом по существу предполагается, что измерения проводятся с бесконечно малыми масштабами разрешения.

Учет конечности масштабов разрешения измерений подразумевает неразличимость координат частиц на этих масштабах и приводит к описанию плазмы на основе многочастичных функций распределения. Этот подход позволяет вычислить вероятность флуктуаций макроскопических параметров и их средние значения. Для замыкания модели используется гипотеза о детальном динамическом равновесии открытой системы с окружающей средой, что позволяет применить к этой системе теорему Лиувилля (о сохранении элементарного фазового объема).

Модель стационарного бесстолкновительного солнечного ветра, построенная в рамках многочастичного подхода, позволяет получить зависимости для макропараметров солнечного ветра (плотности и скорости), совпадающие с результатами двухчас- тичной кинетической модели [4]. При этом наблюдаемое ускорение солнечного ветра в плоскости эклиптики воспроизводится в отличие от одночастичных и гидродинамических моделей только за счет энергии теплового движения частиц у основания солнечной короны, где плазма предполагается равновесной. Этот эффект «дополнительного» ускорения потока плазмы в рамках многочастичного статистического подхода связан с учетом конечных масштабов разрешения измерений, полагаемых много большими масштаба межчастичного взаимодействия в плазме.