Исследование корреляционных характеристик микрогеометрии поверхности трения износостойких порошковых покрытий

Статистические закономерности, описывающие макроструктуру газотермического покрытия, проявляются и в процессе его изнашивания. При этом следует выявить, как особенности строения порошкового покрытия будут проявляться в процессе изнашивания его поверхности трения. Важной задачей является установление корреляционных характеристик профиля поверхности трения, описывающих взаимосвязь элементов микрогеометрии - выступов, неровностей поверхности трения.

Целью настоящей работы является расчет корреляционных характеристик микрогеометрии поверхности трения порошковых покрытий на основе разработки и использования статистической модели Монте-Карло изнашивания порошковых покрытий и материалов при трении скольжения.

Модель Монте-Карло. Для построения статистической модели Монте-Карло выбрана схема трения скольжения, которая используется в усталостной теории износа [1, 2]; рассмотрено трение двух тел с номинально плоскими поверхностями, одно из которых имеет порошковую истираемую поверхность, другое - жесткое и шероховатое. Методом Монте-Карло моделируется процесс установившегося изнашивания порошкового материала в его двумерном сечении, перпендикулярном пути трения. Начальное сечение порошкового материала задается матрицей вероятностно геометрической системы

размера n х m , каждый элемент которой заполняется частицей порошкового материала. При n~m можно описывать процесс установившегося изнашивания порошкового материала, при n< - порошкового покрытия. Верхний слой частиц описывает поверхность изнашиваемого порошкового покрытия и материала, начальная поверхность является гладкой. Путь трения, как параметр процесса изнашивания, разделен на дискретные шаги. На каждом шаге удаляется одна граничная частица с вероятностью, обратно пропорциональной ее статистическому весу, который определяется текущим состоянием макроструктуры изнашиваемой поверхности и является ее локальной характеристикой. Получаемые таким образом матрицы описывают изменение микрогеометрии поверхности изнашиваемого порошкового покрытия и материала на каждом шаге процесса изнашивания.

Через v j обозначен статистический вес частицы поверхности, находящейся в j -ом столбце матрицы модели; вводится вероятность удаления частицы, которая выражается формулой:

где

Г

p j

v

j

V

X -1

^Ц 1

•I- i=1 v. i )

,

m

Z и=* v)

- 1

- нормировочный множитель.

Очевидно, что для вероятностей (1) выполня-

m ется условие нормировки: ^ p j = 1. Рас- j=1

смотрены два способа выбора статистического веса. В первом случае в качестве статистического веса взята сумма X _пр ⁽ + к _по® ( ⁼ •• ■’ ) продольного и поперечного координационных чисел частицы. Ввиду того, что у частиц поверхности X _по ⁽ =1, то статистический вес граничных частиц запишется виде формулы:

V. j

= 1 + X пр

( j )

Для корректного расчета координационных чисел λ пр ⁽¹⁾ и λ пр ^(m) введены циклические граничные условия, связывающие между собой первый и последний столбцы матрицы.

Второй способ выбора веса связан с глубиной нахождения граничной частицы, статистический вес задается соотношением:

V. = 1 + к.

j              j

где к - число удаленных частиц в j-м столбце.

Сравнение с экспериментальными данными. В качестве объектов трибологического исследования выбраны износостойкие элек-трометаллизационные покрытия из порошковых проволок разработки Института физикотехнических проблем Севера СО РАН. Испытания на износ покрытий проводились на машине трения СМЦ-2; на основе анализа работ выбрана схема трения «диск-колодка». Режим испытаний: нагрузка 38 кГ, частота вращения вала 5 об/сек; трение сухое. Образцы для испытаний представляли собой диски диаметра 0,05 м и высотой 0,01 м с порошковым покрытием толщиной до 0,001 м. Исследование поверхности трения проводилось с помощью профилометра SJ-201P фирмы «Mitutoyo» (Япония) в режиме установившегося износа через каждые 4500 циклов трения, на четырех маркированных диаметрально противоположных участках покрытия образца.

Пусть поперечная профилограмма поверхности трения порошкового покрытия задается случайной функцией PR(x). Для определения корреляционных характеристик микрогеометрии по профилограммам введем функцию GV(x) = max(PR(x))- PR(x) значение которой представляет собой глубину выемки в точке x, образованной в результате изнашивания образца. Из анализа микрогеометрии поверхности трения предполагается, что значение функции GV(x) при x=x0 существенно не отличается от значений глубин выемок в точках некоторой достаточно малой окрестности точки x0. Для адекватного описания профиля изнашиваемого покрытия требуется использование весов частиц, учитывающих микрогеометрию окрестности точки износа, примером такой модели является модель с весом (2). Продольные координационные числа λj несут информацию о состоянии соседних столбцов матрицы вероятностно-геометрической системы, описывающей макроструктуру поверхности покрытия. Это приводит к наличию устойчивой корреляции между соседними выемками профиля поверхности трения. Расчеты, проведенные по модели со статистическим весом (3) также подтверждают наличие корреляции между близко расположенными выемками профиля поверхности трения. На рис.1 приведен график усредненной по 100 реализациям модели автокорреляционной функции (рис. 1, график 3), показывающей тесноту корреляционной связи между двумя сечениями профиля на расстоянии d.

Исследованиями выявлено, что в данных корреляционных характеристик наблюдается умеренный статистический разброс, теснота корреляционной связи r монотонно падает с увеличением расстояния d между различными сечениямих x и у функций GV . При d< 100 мкм наблюдается сильная корреляционная связь. При 100 мкм 200 мкм умеренная. При d>3 00 мкм случайные функции GV(x) и GV(y) являются практически независимыми.

Выводы:

• 1.    Статистическим моделированием и математической обработкой экспериментальных данных профиля поверхности трения порошковых покрытий определены автокорреляционные функции микрогеометрии поверхности трения. В качестве случайной характеристики поверхности трения предложено использовать функцию глубины выемок.

• 2.    Проведены расчеты корреляционной характеристики микрогеометрии поверхности трения порошковых покрытий с использованием статистической модели Монте-Карло изнашивания порошковых покрытий и материалов при трении скольжения со статистическим весом частиц, связанным с координационными числами частиц. Расчетная кривая качественно согласуется с графиком экспериментальной автокорреляционной функции. Для более точного описания корреляционной характеристики поверхности трения порошковых покрытий обосновано использование модели Монте-Карло со статистическим весом, равным полному координационному числу частиц.

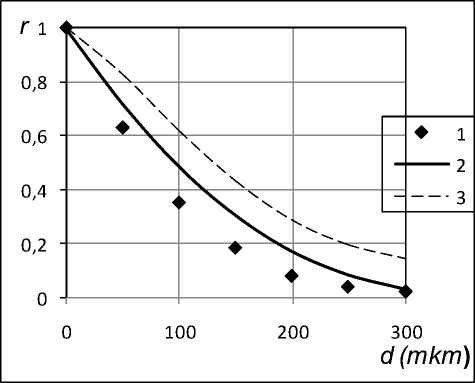
Рис. 1. Корреляционные характеристики микрогеометрии поверхности трения порошковых покрытий:

1 – экспериментальная усредненная автокорреляционная функция, полученная обработкой профилограмм при 1323 м пути трения; 2 – расчетная автокорреляционная функция; статистический вес равен полному координационному числу частиц (усреднение по 100 реализациям модели); 3 – расчетная автокорреляционная функция; статистический вес равен сумме продольных и поперечных координационных чисел частиц