Исследование кривошипно-кулисного механизма с дезаксиальной кулисой

В технике встречаются механизмы, преобразующие равномерное вращательное движение в неравномерное. Это необходимо по следующим причинам:

• -    для уменьшения отрицательного воздействия большой скорости на технологический процесс (например, при обработке металлов резанием);

• -    для уменьшения времени рабочего цикла механизма, имеющего небольшую нагрузку с тем, чтобы облегчить работу других более нагруженных механизмов.

Одним из механизмов, обеспечивающих неравномерное вращение, является кулисный механизм с вращающейся кулисой. В работе [1] дан кинематический анализ двухкривошипного шарнирного четырехзвенника, выходной кривошип которого совершает вращательное движение с переменной скоростью. Выявлено влияние длин звеньев механизма на кинематику его движения. В том случае, когда требуется получить более высокий коэффициент неравномерности, чем его имеет двухкривошипный четырехзвенник, можно применять кулисный механизм. Как известно, в этом механизме коэффициент неравномерности вращения зависит от длины стойки. Чем короче стойка, тем меньше коэффициент неравномерности. Для получения вращательного движения кулисы длина стойки должна быть меньше длины кривошипа.

Одной из разновидностей кулисного механизма является кривошипно-кулисный механизм с дезаксиальной кулисой. У этого механизма направление кулисы не совпадает с ее осью вращения. Такого вида механизм применяется в гребнечесальной машине фирмы «Хартфорд». Рассмотрим кинематику такого механизма, исследовав его аналитическим методом.

Введем следующие обозначения: r - длина кривошипа, a - длина стойки, e -дезаксиал кулисы, l - переменная длина кулисы, а - угол поворота кривошипа, ф -угол поворота кулисы.

Представим механизм в виде замкнутого векторного контура (рис. 1) и запишем векторное уравнение [1]:

r + а = e + l .                                            (1)

Спроектировав это уравнение на оси координат, получим:

r cos а = e cos ф +l cos(ф + 90°), а + r sin а = esin ф +l sin(ф + 90°).

Запишем эти уравнения в другом виде:

r cos а = e cos ф - l sin ф ,

.      •                                                                                  (3)

а + r sin а = e sin ф + l cos ф .

Выразив из первого уравнения значение sin ф и подставив его во второе, будем иметь:

re r sin а +--cos а + a ф = arccos--------2l----------.                             (4)

— + l

l

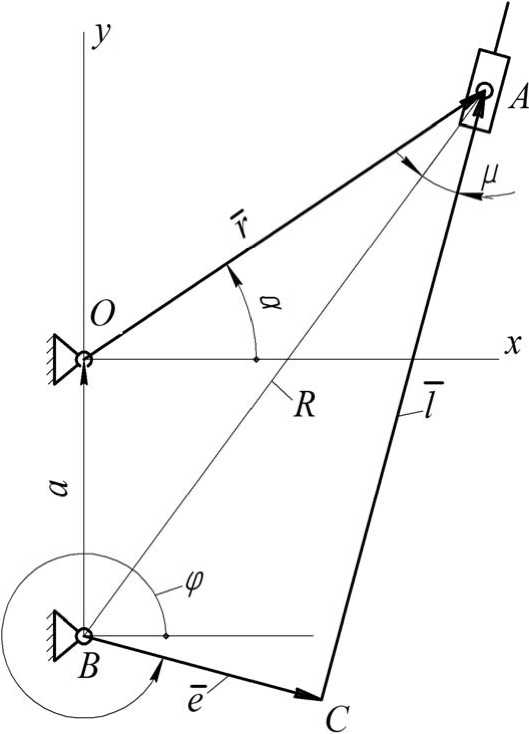
Рисунок 1

Из треугольника ОАВ (рис. 1) получаем радиус вращения точки А на кулисе относительно оси В:

R = r ² + а ² - 2 ra cos( а + 90 ° ) = V r ² + a ² + 2 ra sin а .               (5)

Величину l найдем из треугольника ВАС:

l = 4R ² - e ² = V r ² + а ² + 2 ra sin а - e ² .                     (6)

Так как а = ю ₀1 , а ф = m t , где m 0 и m - угловые скорости кривошипа и кулисы, то после дифференцирования уравнений (3), получим:

m0 r sin а = me sin ф + v sin ф + ml cosф, m0r cosa = mecosф + vcosф - ml sinф.

dl

Здесь v = dt- скорость скольжения камня по кулисе.

Повернем оси координат на угол ф в сторону, обратную отсчету угла ф , и получим следующие выражения:

ω ₀ r sin( α - ϕ ) = ω e sin( ϕ - ϕ ) + v sin( ϕ - ϕ ) + ω l cos( ϕ - ϕ ), ω ₀ r cos( α - ϕ ) = ω e cos( ϕ - ϕ ) + v cos( ϕ - ϕ ) - ω l sin( ϕ - ϕ ).

Или

ω r sin( α - ϕ ) = ω l , ⁰                                                                   (9)

ω ₀ r cos( α - ϕ ) = ω e + v .

Из этих уравнений находим ω и v :

ω r sin( α - ϕ ) ω = ⁰           ,

l v = ω0rcos(α-ϕ) -ωe.

Продифференцируем первое уравнение выражения (7):

ω02rcosα = ω2 e cosϕ+ ar sinϕ+ ωv cosϕ+ εl cosϕ+ ωv cosϕ- ω2l sinϕ, dv где ar =    - относительное ускорение при скольжении камня по кулисе.

dt

После поворота осей х и у на угол ϕ имеем:

ω ₀ ² r cos( α - ϕ ) = ω ² e + 2 ω v + ε l .

Отсюда находим угловое ускорение кулисы:

ω ² r cos( α - ϕ ) - ω ² l - 2 ω v

ε = ⁰            l               ,                                   (11)

где ω ² l - нормальное ускорение точки С, 2 ω v - ускорение Кориолиса.

На рис. 2 и 3 представлены кривые изменения угловой скорости и углового ускорения кулисы, подсчитанные по формулам (10) и (11) при следующих относительных параметрах механизма: ω ₁ = 1 ; r = 1 ; a = 0,5 ; e = 0,25 . Анализ кривых показывает, что угловая скорость кулисы при α = 0 ÷ 180 ° изменяется незначительно и в первом приближении движение кулисы можно считать равномерным, что иногда требует технологический процесс обработки материалов. Найдем коэффициент неравномерности вращения кулисы для данного случая.

Из рис. 2 видно, что максимальное значение угловой скорости кулисы равно 1,95, а минимальное – 0,65. Коэффициент неравномерности определяется по формуле:

k ₌ ω макс - ω мин ₌ 1,95 - 0,65 ₌ 1 ω _ср           1,3

С уменьшением длины стойки и увеличением дезаксиала коэффициент неравномерности возрастает.

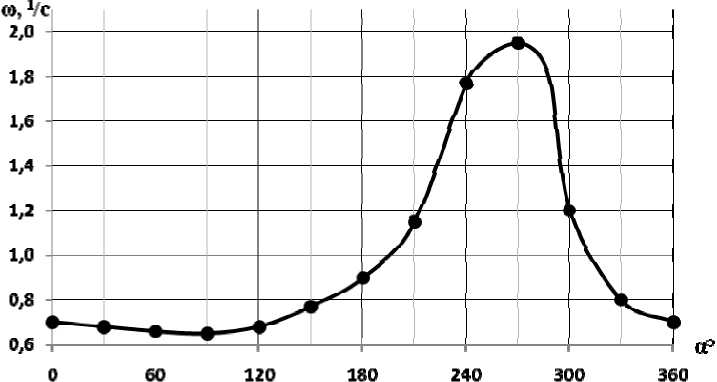
Рисунок 2

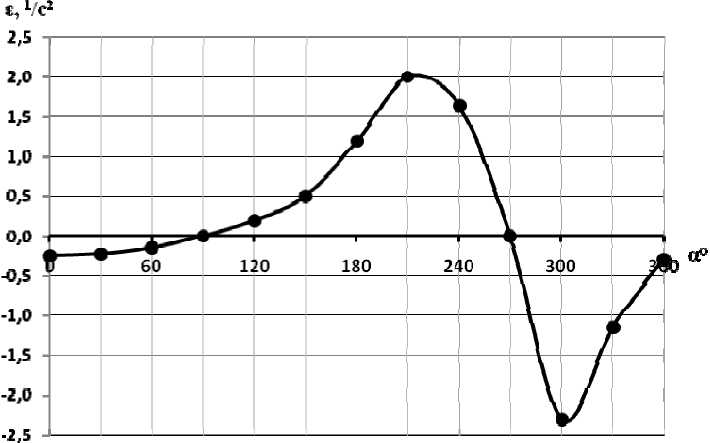
Рисунок 3

Запишем формулу (12) в другом виде, подставив в к значение ю ср

^Ю макс ^{+ Ю} мин

к =

ю - to макс     мин

ю + ю макс мин

Из этой формулы следует, что при ^ю мин = 0 к = ² , а при ^ю мак_с = ^ю мин к = 0 . Это говорит о том, что у механизмов с остановками выходного звена к = 2 .

Таким образом, найдены все угловые характеристики кулисы: ю и е .

Так как в механизме большую роль играет угол давления, то найдем экстремальные значения этого угла для механизма, имеющего следующие параметры: r = 1 ; a = 0,5 ; e = 0,25 . Угол давления ц - это угол между направлением кулисы и радиусом точки кулисы, совпадающей с камнем. Из треугольника АВС его величина равна:

e ц = arcsin—. R

Следовательно ee

цтах = arcsin---- и ат = arcsin----. max                       min min                       max

Найдем производную от выражения (5) и приравняем ее нулю:

/ I 2 . 2 . n : V ar cos а _А

(л! а + r + 2 аг sin а ) = .                  = = 0 .

V a ² + r ² + 2 ar sin а

Отсюда cos а = 0 , а 1 = 90 ° , а ₂ = 270 ° .

Находим значения      R max      и      R m_in .      R max = V a ² + r ² + 2 ar = 1,5 ;

^R min = V a ² + r ² - ^{2 ar} = ^0,5 . Получаем экстремальные значения угла μ:

0,25

Ц max = arcsine = ³⁰ ° ,

A min

= arcsin ^’ ^^ = 9 ° 36 '.

1,5

Если принять максимально допустимое значение угла давления, равное 30 °, то данный механизм будет работать в относительно легких динамических условиях. Очевидно, что с увеличением дезаксиала этот угол также будет возрастать и механизм, у которого e >  0,25 r и a = 0,5r , использовать нецелесообразно.

ВЫВОДЫ

• 1.    Анализ замкнутых векторных контуров позволил провести кинематический анализ кривошипно-кулисного механизма с вращающейся дезаксиальной кулисой.

• 2  .Анализ результатов исследований показал, что в течение определенного

• 3.    Найдено влияние длины стойки и дезаксиала на коэффициент неравномерности и угол передачи.

времени вращающаяся кулиса имеет движение, близкое к равномерному.