Исследование квазиоптических структур из искусственного диэлектрика в СВЧ-диапазоне

Линзы из неоднородного диэлектрика известны давно. Однако изготовление таких линз наталкивается на технологические трудности и часто затраты на производство материалов с изменяющимися вдолькоординат диэлектрическими параметрами слишком высоки. В некоторых случаях неоднородный диэлектрик можно представитьв виде некоторой структуры из однородного диэлектрика, применяя специальные алгоритмы перфорации материала, каки некоторые другие способы.

Сферическая линза Люнеберга . В общем случае линза Люнеберга представляет собой диэлектрическую сферу, в которой коэффициент преломления n зависит от радиуса по следующему закону [1]:

² n ( r ) = 2 -^{⎛ r ⎞} , (1)

⎜⎝R ⎟⎠ где R – радиус сферы; r – расстояние от центра линзы. Такая сфера преобразует сферический волновой фронт облучателя в плоский. Линза Люнеберга позволяет осу-ществлятьсканирование в полном пространственном ди- апазоне углов без искажения диаграммы направленности (ДН). Сканирование в сферической линзе обычно осуществляется переключением нескольких облучателей, расположенных на ее поверхности. Линза Люнеберга является идеальным устройством для широкоугольного неискаженного сканирования. Этим объясняется большой интерес, который проявляется к линзам данного типа.

Ранее были рассмотрены варианты создания искусственного диэлектрика и линз Люнеберга из материала с постоянной диэлектрической проницаемостью [2; 3]. Вид одной из моделей в разрезе приведен на рис. 1.

Модельсостоит из множества слоев диэлектрика вдоль радиуса по вертикали, с изменением диаметра слоя вдоль радиуса линзы по горизонтали. Вертикальному и горизонтальному направлениям соответствуют направления осей y и z на рис 2. Вариация диаметра слоя диэлектрика имитирует изменение n вдольрадиуса линзы. Для исследований был использован материал с ε= 1,6 . Возможно использование другого материала – в зависимости от ε материала будет изменяться положение фокуса линзы.

Моделирование производилосьпри помощи CST Studio Suite.

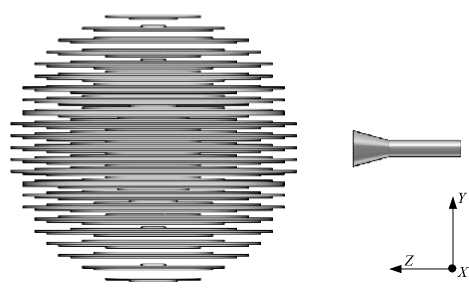
Рис. 1. Модельлинзы Люнеберга из слоев материала с постоянной диэлектрической проницаемостью в разрезе

Расчетный рабочий частотный диапазон антенны 20…30 ГГц. Диаметр линзы составляет 160 мм, возбуждение производится коническим рупором с уровнем облучения края линзы –10 дБ. КНД на частоте 25 ГГц составил 30,7 дБ. Уровень боковых лепестков в диапазоне 20…30 ГГц в плоскости Е не более –17,5 дБ, в плоскости Н не более –19,5 дБ. Расчетная зависимостьКНД антенны от частоты приведена на рис. 2.

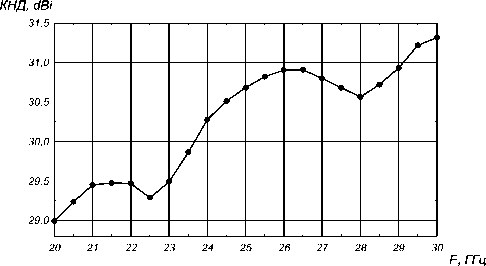
Рис. 2. Расчетная частотная зависимостьКНД-антенны

С целью экспериментального исследования было выполнено макетирование антенны (рис. 3). Для изготовления макета был применен вспененный полимер с е = 1,6. Конструкция макета позволяет осуществлятьизмерение характеристик линзы при различных углах облучения с шагом изменения угла в 8°.

Рис. 3. Фотография макета линзы Люнеберга

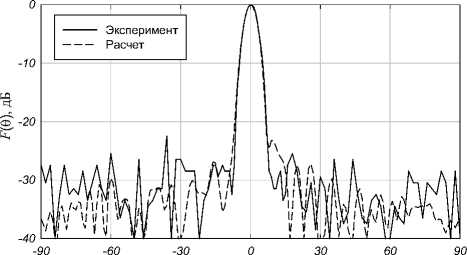
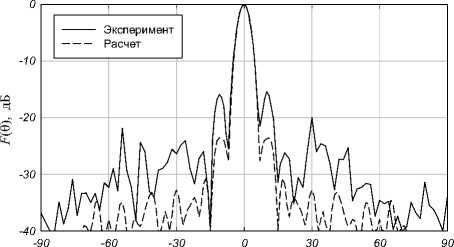
Расчетные и экспериментальные ДН в плоскостях E и Н приведены на рис. 4 и 5. Плоскости Е соответствует вертикальная плоскость ( YOZ ), плоскости H – горизон-

XZ 1

6,°

Рис. 4. ДН линзы Люнеберга в плоскости Е

6,°

Рис. 5. ДН линзы Люнеберга в плоскости H

Так как особый интерес представляет способность линзы Люнеберга осуществлятьсканирование, были рассчитаны и затем измерены ДН для отклонения облучателя в плоскости Е . Измерения ДН проводилисьдля случаев облучения линзы под углом от 0 до 24° с шагом в 8°. ДН в плоскостях E и Н для случая облучения под углом в 24° 6 7

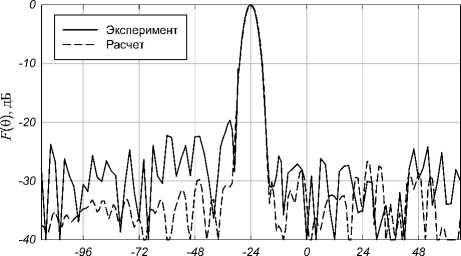
6,°

Рис. 6. ДН линзы Люнеберга в плоскости Е для случая облучения под углом в 24°

Анализируя ДН антенны, можно заметить, что уро-веньбоковых лепестков (УБЛ) ДН макета в плоскости H выше, чем УБЛ ДН модели, однако он не поднимается выше –16,2 дБ, что во многих случаях является приемлемым. Объяснитьданные расхождения можно тем, что в модели не были учтены все конструкционные особенности макета, возникшие в процессе изготовления.

Цилиндрическая линза Микаэляна. Для сокращения продольных размеров излучающей структуры с облучателем и линзой необходимо, чтобы облучательвплотную примыкал к поверхности линзы. Такая конфигурация реализуется в линзе Микаэляна, представляющей собой фрагмент горизонтально-слоистой неоднородной среды, диэлектрическая проницаемостькоторой зависит от вертикальной координаты по закону [1]:

ε ( y ) =

ε ₀

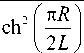
где ε ₀ – диэлектрическая проницаемость на оси линзы; R – вертикальная (в случае цилиндрической линзы радиальная) координата (расстояние до оси линзы); L – толщина линзы. Распространяясьвдольтакой среды, волна многократно фокусируется на оси с пространственной периодичностью 2 L . При этом в плоскости, перпендикулярной оси и лежащей посередине между фокусами, распределение поля становится синфазным.

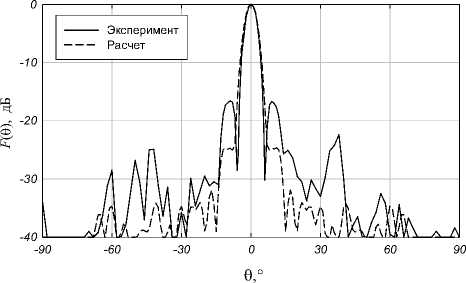
Рис. 7. ДН линзы Люнеберга в плоскости H для случая облучения под углом в 24°

Был осуществлен расчет линзы Микаэляна из перфорированного диэлектрика. Значения е, как следует из (2), лежат между ε0 и 0. Реализоватьсреду с ε<1 невозможно, поэтому ε(y) следует ограничитьпо уровню 1. При этом отношение диаметра линзы к ее толщине определится выражением d = 4arch (ε0 )

L π

Создатьискусственно неоднородный диэлектрик мож- но при помощи отверстий переменного диаметра в однородном диэлектрике. При этом возникает технологическое ограничение на размер отверстий: стенки мате- риала между ними должны сохранятьпредельную минимальную толщину для обеспечения механической прочности. Если принятьминимальную толщину стенок равной 1 мм, это приводит к ограничению n по уровню 1,1, что влечет за собой увеличение толщины линзы. Для обеспечения минимальной толщины стенок форма отверстий должна бытьшестиугольной (рис. 8).

Зависимость «радиуса» шестиугольного отверстия r (параметр, соответствующий радиусу описанной вокруг шестиугольника окружности) от требуемого значения эффективной диэлектрической проницаемости εэф может бытьнайдена при предположении, что εэф определяется разностью объемов отверстия и элементарной шестиугольной ячейки (см. рис. 8). Для расчета требуется знать обратную зависимость r(εэф), которая определяется следующим образом [3]:

/ \ ^ε 0 ^{- ε} эф ₍₄₎ r ( ε эф ) = r я vε ₀ - 1

где r _я – размер шестиугольной ячейки с отверстием, который является постоянной величиной, много меньшей длины волны (см. рис. 8). Подставляя в (4) вместо ε _эф значение ε ( y ) из (2), получаем зависимость r от R . Следует заметить, что ε ₀ равна диэлектрической проницаемости однородного материала, из которого изготавливается линза.

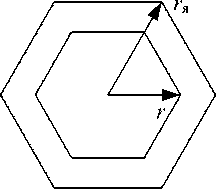
Рис. 8. Гексагональная ячейка с отверстием

Возможно применение отражающей конфигурации линзовой антенны, что позволяет вдвое сократитьее продольные размеры. При этом со стороны, противоположной облучателю, располагается плоский металлический отражатель (рис. 9).

отражатель

облучатель

Рис. 9. Трехмерная модельантенной системы с линзой Микаэляна отражатель

облучатель

Рис. 10. Диаграмма распределения фазы электрического поля

0,°

Рис. 11. ДН в плоскостях Е и Н для 12 ГГц

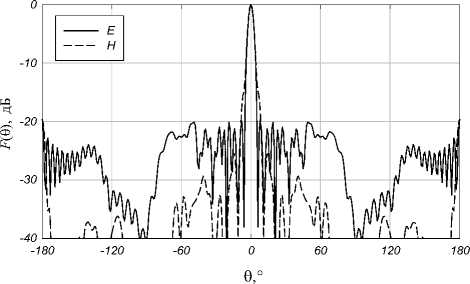
Рис. 12. ДН в плоскостях Е и Н для 24 ГГц

При моделировании антенной системы были заданы следующие параметры:

– диапазон частот – 12…24 ГГц;

– диаметр линзы – 150 мм (6–12 л);

• –    толщина линзы – 72 мм;

• –    «радиус» элементарной ячейки – 2,8 мм;

• -    s ₀ -2,9 (органическое стекло);

  –тип облучателя – открытый конец волновода;

  – абочийдиапазончастотоблчателя– 12 24 ГГц

В области низких частот имеет место излучение мощности с боковой поверхности линзы, что связано с шириной ДН облучателя на низкой частоте. С этим же связано и снижение КИП в области низких частот. Очевидно, что в идеальном случае облучатель должен иметь частотнонезависимую ДН и стабильный фазовый центр.

-10

-20

-30

E

H

И №й

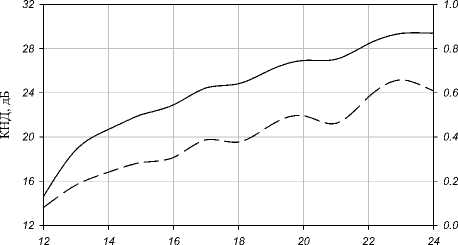
f , ГГц

Рис. 13. ЗависимостьКНД и апертурного КИП от частоты

-40

-180       -120        -60

ДН для крайних частот исследуемого диапазона, а также частотные зависимости коэффициента направленного действия (КНД) и коэффициента использования поверхности (КИП) приведены на рис. 11–13.

Антенная система показывает приемлемый уровень бокового излучения, особенно в области высоких частот.

Таким образом, моделирование и экспериментальное исследование линзовых антенн из искусственно созданного неоднородного диэлектрика показывают воз-можностьих осуществления в СВЧ-диапазоне. Результаты экспериментов подтверждают адекватностьисполь-зуемых предположений и дают удовлетворительные совпадения с расчетами.