Исследование логико-математической модели вычислительной сети

Введение. Имитационное моделирование - это метод исследования объектов, основанный на том, что изучаемый объект заменяется имитирующим объектом. Эксперименты проводятся с имитирующим объектом, а в результате получают информацию о самом объекте.

Исследование. Нами исследовалась модель вычислительной сети с применением имитационного моделирования.

Для реализации имитационной программы нами использован модуль SMPL для языка Object Pascal и среда разработки Delphi7, обладающая всеми необходимыми функциями для реализации программы и пользовательского интерфейса.

Данная модель актуальна, поскольку вычислительные сети используются во многих организациях и на производстве. С помощью этой модели возможно проиллюстрировать все достоинства и недостатки рассматриваемой вычислительной сети, а применяемый способ реализации позволяет провести эксперименты для анализа модели, что позволит улучшить её.

В рассматриваемой вычислительной сети система обработки информации содержит мультиплексорный канал и N мини-ЭВМ. На вход канала через интервалы времени 10±2 микросекунд поступают сообщения от датчиков. В канале они буферизируются и предварительно обрабатываются на протяжении 12,5±2,5 микросекунд. Потом сообщения поступают на обработку в ту мини-ЭВМ, которая имеет наименьшую длину входной очереди. Емкости входных накопителей всех мини-ЭВМ рассчитаны на хранение пяти сообщений. Если в момент прихода сообщения входные накопители всех мини-ЭВМ полностью заполнены, то сообщение получает отказ. Время обработки сообщения во всех мини-ЭВМ равно 300 микросекунд.

Есть две возможности уменьшения числа сообщений, получающих отказ:

• •    увеличение емкости входных накопителей ЭВМ;

• •    ускорение обработки сообщений в ЭВМ при достижении суммы

длин очередей во всех ЭВМ некоторого порогового значения (авральный режим).

Переключение ЭВМ в авральный режим происходит тогда, кода суммарное количество сообщений во входных накопителях всех миниЭВМ достигает значения 18. В этом случае все мини-ЭВМ уменьшают время обработки сообщения на k ( k <300) микросекунд, что требует k х 5 единиц стоимости на каждое сообщение. Все мини-ЭВМ в авральный режим переводятся одновременно.

Убытки за каждое сообщение, которому отказано в обработке, оставляют 130 единиц стоимости, единица времени работы одной ЭВМ в авральном режиме обходится в 3 единиц стоимости.

Перед нами стояла задача в ходе исследования выяснить при какой авральной скорости обработки сообщений достигается минимум суммарных затрат (убытков от отказов сообщениям в обслуживании, затрат на увеличение емкости входных накопителей и затрат на поддержку аврального режима).

С целью описания функционирования системы была построена Q-схема, изображенная на рисунке 1.

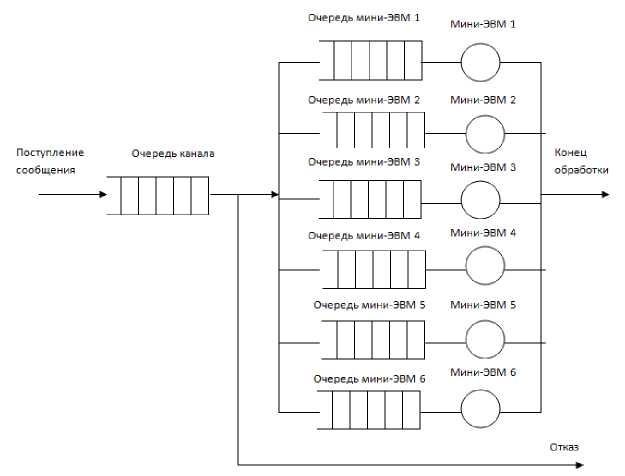
Рисунок 1- Q-схема

Схема иллюстрирует, что при поступлении сообщения, оно сразу ставится в очередь канала, после этого, если очереди всех миниЭВМ заняты, в рассматриваемом случае емкость равна 5, то сообщение получает отказ и не обрабатывается, в противном случае выбирается мини-ЭВМ с минимальной длиной очереди. Далее сообщение ставится в очередь выбранной мини-ЭВМ, затем обрабатывается этой мини-ЭВМ. На этом обработка сообщения заканчивается.

Граф-схема модели представлена на рисунке 2.

В результате анализа системы было выделено четыре события:

• 1-    событие «поступление сообщения и постановка его в очередь канала»;

• 2-    событие «окончание обработки в канале и постановка сообщения в очередь мини-ЭВМ»;

• 3-    событие «планирование окончания обработки сообщения в мини-ЭВМ»;

• 4-    событие «конец моделирования».

  

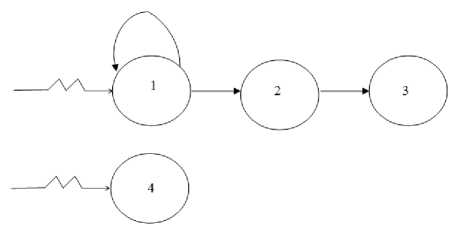
  Рисунок 2 - Граф-схема модели

  В самом начале моделирования наступает

  
  

событие

«поступление сообщения», оно многократно повторяется при поступлении нового сообщения, в этом же событии происходит постановка сообщения в очередь канала. Через промежуток времени наступает событие «окончание обработки сообщения» в канале и постановка его в очередь мини-ЭВМ. Далее через промежуток времени происходит событие планирования окончания обработки сообщении в мини-ЭВМ.

Константами в данной программе являются, четыре события моделирования, которые описаны следующим образом:

• •    evGen=1 – событие приход сообщения и постановка его в

очередь канала

• •    evRes=2 – окончание предварительной обработки и

• постановка сообщения в очередь мини-ЭВМ

• •    evRel=3 – планирование окончания обработки сообщения в мини-ЭВМ

Для работы с транзактами был описан тип tranzacts представляющий собой запись из полей:

• •    num: longword – номер транзакта

• •    dev: P_Device – устройство, в котором транзакт

обрабатывается

• •    och: P_Queue – очередь, в которой находится транзакт

Канал в коде описан как D: P_DEVICE, а мини-ЭВМ массивом устройств Dd: array [1..6] of P_DEVICE. Аналогичным образом обозначены очереди. Для того, чтобы отследить сколько сообщений получили отказ была объявлена очередь, в которую и помещались сообщения, не обрабатывающиеся в мини-ЭВМ по причине занятых накопителей. Очередь отказа - Qo:P_QUEUE.

Структура программы представляет собой процедуру Smplmodel, в которой и происходит моделирование с использованием цикла repeat - until EVENT = evEnd, в котором с помощью case определяется какое событие моделирования должно наступить, а также процедуры Button1Click. В этой процедуре по нажатию кнопки запускается процедура Smplmodel в цикле с изменяющимся параметром k в новом прогоне на 10. В итоге получается 16 прогонов, результат которых выводится в компоненте memo, а также строится график и гистограмма.

Для исследование модели было разработано также приложение, позволяющие просмотреть данные по прогонам, а также графики и гистограммы, используя которые можно проанализировать результат моделирования.

Интерфейс программы выглядит следующим образом (Рис.3):

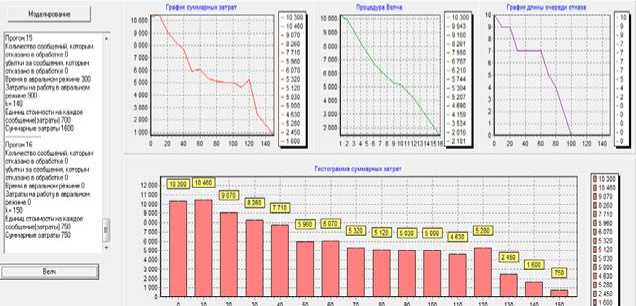
Рисунок 3 - Интерфейс программы

По нажатию на кнопку «Моделирование» запускается процедура моделирование, выводится результат по прогону, строятся графики и гистограмма. После нажатия на кнопку «Велч» запускается процедура Велча и её результат выводится на графике.

Также в программе предусмотрен вывод статистики в текстовый файл, который автоматически создается в папке, где находится программа.

В результате прогонов с исходными данными получился отчет (рисунок 4).

Показатель, который больше всего нас интересует максимальная длина очереди отказа, то есть скольким сообщения отказано в обработке. В данном случае это 10 заявок. Для функционирования реальной системы этот показатель слишком большой, потому что приводит к огромным затратам.

Время моделирования 700 тактов.

Устройства

! Имя устройства ] Ср.вр.зан

% зан.вр. ! Кол. запр.

kanal ! mim'EBM_l J miniEBM_2 ! mim'EBM_3 ; miniEBM_4 ; miniEBM_5 ; mim’EBM_6 j

9. 32

167.25

273.00

150.00

300.00

300.00

300.00

74. 571 95.571 39.000 42.857 42.857 42.857

42.857

56 ;

очереди

] имя очереди	ср.вр. ожидания 1	ср. кв. ; откл.	мах 1	длина средняя ;	текущая ;
! ochered kanalа ;	o.o7 ;	0.255 ;	1 ;	о.о1 ;	о :
1 ochered otcaza ;	—	—	ю ;	1.22 ;	ю ;
ochered 1 ;	378.20 ;	200.770 ;	6 :	з.4з ;	5 ;
ochered 2 I	i32.oo ;	132.000 ;	5 ;	1.53 ;	5 ;
ochered 3 ;	152.00 :	112.573 ;	5 ;	1. si :	5 ;
ochered 4 ;	144.50 :	144.500 !	5 ;	1.47 :	5 ;
ochered 5 I	145.00 :	145.000 !	5 ;	1.4з :	5 ;
ochered_6 I	143.50 :	143.500 !	5 1	1. 38 !	5 :
1		---------	------+-

Рисунок 4 - Расчет характеристик системы

Для определения режима функционирования с помощью процедуры Велча, нами было сделано следующее:

• 1.    Выполнено n повторных прогонов имитационной модели ( n >  5), продолжительность каждого из которых равна т (где т — большое число). Пусть Y ij представляет данные i -го наблюдения в ходе j -го повторного прогона имитационной модели ( = 1,2,..., n ; i = 1, 2,..., т).

• 2.    Усредненный процесс имеет средние и дисперсии . Следовательно, усредненный процесс имеет ту же кривую переходного среднего, что и начальный процесс, но его график имеет лишь (1/ n )-ю дисперсию.

• 3.    Чтобы выровнять высокочастотные колебания в процессе, мы определяем скользящее среднее (где w - это окно; w является положительным целым числом из условия).

• 4.    Создали график для i= 1,2,..., т - w и выберите l как значение i, за которым очевидно схождение процесса

Поэтому, если i не очень близко к началу повторных прогонов модели, то является всего лишь простым средним 2 w + 1 наблюдений усредненного процесса, центрированного по наблюдению i . Оно называется скользящим средним, поскольку i перемещается во времени.

Результат применения процедуры Велча (Рис.5):

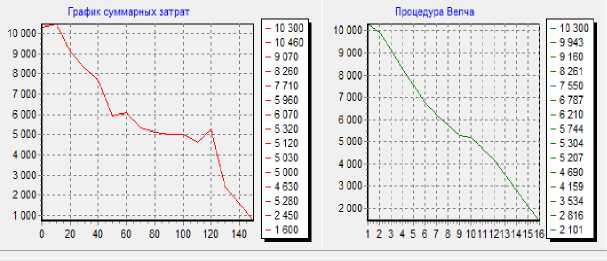
Рисунок 5 - График, иллюстрирующий результат применения процедуры Велча

Так как в представленной модели изменение выходного параметра - суммарных затрат зависит только от значения параметра k, то матрица плана экспериментов будет иметь вид, представленный в таблице 1:

Таблица 1. План эксперимента

Номер опыта	Значение параметра k	Выход y
1	0	10 300
2	10	10 460
3	20	9 850
4	30	9 700
5	40	9 030
6	50	9 430
7	60	8 920
8	70	8 770
9	80	8 800
10	90	8 010
11	100	7 400
12	110	6 790
13	120	6 540
14	130	4 250
15	140	2 080
16	150	750

Результат моделирования представлен на гистограмме (Рис. 6) и графиках (Рис. 7, 8), на которых очевидно, что при повышении параметра k, а, следовательно, уменьшении авральной скорости обработки, снижаются суммарные затраты.

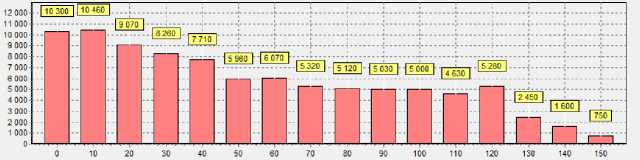
Рисунок 6 - Гистограмма суммарных затрат

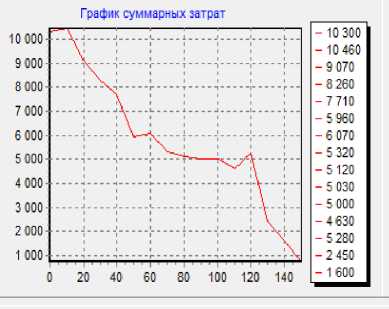
Рисунок 7 - График суммарных затрат

Из графика длины очереди отказа видно, что как только k=100, то ни одно сообщение не получает отказ.

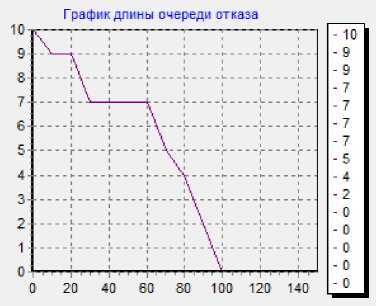
Рисунок 8 - График длины очереди отказов

Выводы. По результатам моделирования оптимальный вариант представлен в прогоне №16, так как при минимальных затратах не отказано ни одному сообщению. Таким образом, минимальная авральная скорость составляет 300-150=150 микросекунд.

В результате выполненного исследования, поставленная задача была успешно решена. В результате исследования построена модель работы вычислительной сети, разработан алгоритм поставленной задачи, построена имитационная модель, проведены имитационные эксперименты, определено при какой авральной скорости суммарные затраты стали минимальны.