Исследование локальных температур на пластически деформирующих зернах при шлифовании с наложением ультразвуковых колебаний

Повышение работоспособности круга и улучшение качества обработанных деталей при шлифовании с наложением ультразвуковых колебаний (УЗК) во многом связано с изменением тепловой напряженности этого процесса. На работоспособность абразивных зерен (АЗ) круга и качество поверхностного слоя детали оказывают влияние, преимущественно, локальные температуры [1]. Однако аналитическое исследование локальных температур при шлифовании с УЗК выполнено для режущих зерен [2]. Для оценки условий работы шлифовального круга необходимо знать локальные температуры от пластически деформирующих зерен [3], однако такие исследования для шлифования с УЗК до сих пор не выполнены.

Моделирование тепловых процессов выполнено для схемы плоского многопроходного шлифования периферией круга. Схематизируя объекты, участвующие в теплообмене, АЗ представили в виде усеченного конуса с углом при вершине 2y и площадкой затупления размером £ 2 . Пограничный слой между АЗ и заготовкой и его термическое сопротивление не учитывали, поскольку контакт между этими телами в условиях пластической деформации приближается к идеальному. Считали, что температура в любой точке на поверхности соприкосновения АЗ и заготовки одна и та же. Для повышения достоверности результатов учтена зависимость сопротивления материала заготовки деформированию и теплофизических свойств всех взаимодействующих объектов от температуры. Мощность тепловыделения при диспергировании заготовки пластически деформирующим АЗ:

Wi = W9 + W2T, где Wd, W2T - мощность тепловыделения источника, возникающего как результат перехода в теплоту работы деформирования (W5) и работы силы трения зерна о заготовку (W2r), Вт.

Мощности источников определены по формулам [4, 5]:

W2T = Pzтр • Vк;

Wd = (Pzi - Pz тр) • V ,

где P zi - касательная составляющая силы диспергирования единичным зерном, Н; P z тр - сила трения между АЗ и заготовкой, Н; V к - рабочая скорость шлифовального круга, м/с.

Для зерен, осуществляющих пластическую деформацию в процессе шлифования с использованием УЗК:

р = c ■ н у 'к ( ^ 0 ^f sin у + cosl ) ■ f _д + ^Утрд ) zi          т                                 кд

² V        Мд )           ³

₌ М ■ f _тд ■ c ■<

^P z тр            3

, где /рд - площадь поверхности трения зерна о заготовку, м2; /кд - площадь поверхности зерна, осуществляющей пластическое деформирование материала заго-узк товки, м2; c - коэффициент [5];н т - предел текучести материала заготовки при скорости и температуре деформации в процессе шлифования и наложении УЗК, Па; Цо - коэффициент трения АЗ о заготовку; у -угол при вершине АЗ, град.

Плотность тепловыделения на участке контакта АЗ с заготовкой приняли распределенной по экспоненциальному закону (аналогично закону распределения нормальных напряжений), а максимальная плотность тепловыделения [4,5]

_      ^W 2 т ‘ k о

^{2 T} Ц* exp [ - k ₀ ^₂] ;

где k o - коэффициент, м^-1; £ 2 - размер площадки затупления на АЗ, м.

Плотность тепловыделения на расстоянии x_и от вершины зерна (точки Е на рис. 1)

q 2 т ( x u ) = q 2т ■ ^exp [^{- k} о ■ x u ] .

Источник плотностью q _д в зоне пластического деформирования материала заготовки (см. рис. 1), считаем распределенным равномерно [4, 5]:

q д =

W ₈ • cos у

f кд

При наложении колебаний в направлении у , перпендикулярном обрабатываемой поверхности, глубину внедрения пластически деформирующего АЗ, определяющую площадь f _щ, можно представить как функцию от расстояния l между вершиной зерна (точка Е ) и начальной точкой F контакта АЗ с заготовкой (см. рис. 1).

a mi ( ¹ ) = a m ( l ) + A y ■ sin ⁽ ®77" + Ф ),

"кр где am (l) - глубина внедрения в заготовку пластически деформирующего АЗ при отсутствии УЗК [5], м; Ay - амплитуда колебаний в направлении, перпендикулярном обрабатываемой поверхности, м; и - циклическая (круговая) частота колебаний, рад/с; ф - фаза УЗК, рад.

Наложение колебаний приводит к качественному изменению процесса диспергирования материала заготовки зернами круга и сопровождается уменьшением пределов прочности и текучести материала [6]. При наложении УЗК предел текучести материала заготовки равен пк

= к -ат тт

где ^к _т - коэффициент, показывающий степень уменьшения ° т при наложении колебаний [6]. Поскольку этот коэффициент меньше единицы, то можно прогнозировать снижение силы диспергирования за счет уменьшения предела текучести материала заготовки.

Считали, что заготовка 1 неподвижна, а АЗ 2 , шлифовальный круг 3 и плоскость сдвига D 1 E перемещаются относительно заготовки со скоростью, равной сумме скоростей V к и скорости продольной подачи V_s пр (см. рис. 1). Система координат х 0 у связана с зерном и перемещается относительно заготовки в отрицательном направлении оси 0 х . Уравнения теплопроводности для пластически деформирующего АЗ 2, заготовки 1 и шлифовального круга 3 (см. рис. 1) представили в следующем виде:

д T1_  1 дГ. д Т УдГ  д Т I     a Т

=I AiI +I А,I — Г дт q • р,  д x (   д x )   д у (   д у )       д x

;

572 дт д Т3 дт

c 2 -Р 2

^с з •Р з

^д | 3 ^{д 7} 2 I . ^д 3 ^{д 7} 2

I AP        I + I А?        I дх(   дx )  дУ (   дУ )

;

^д I 7 ^д Т I । ^д 7   ^д Т з

I Аз        I + I Аз I дx (   дx J  ду(   дУ )

где Х 1 , Х 2 , Х з - коэффициенты теплопроводности, Вт/(м • К); с i , с 2 , с з - теплоемкости, Дж/(кг К); p i , р 2 , р з , - плотности, кг / м³; Т i , Т 2 , Т з , - температуры заготовки, АЗ, шлифовального круга соответственно, К; т - время, с.

Начальное условие

Т(x, у, О) = То означает равенство в начальный момент времени температур любой точки заготовки, АЗ, и круга температуре окружающей среды. Условия взаимодействия поверхностей обрабатываемой заготовки, АЗ и круга описываются следующими граничными условиями:

- в пределах зоны контакта EV АЗ 2 с заготовкой 1 :

6 Т_{к =} q 9 Т = - q^

ду     А1   дуА

,,

Т, = Т. q2Т + q2Т = q2Т . 1         2,

- в пределах зоны контакта D 1 E АЗ 2 с заготовкой 1 :

^ _^ дТ^ ₌ _^^ д n     А 1 д n А ₂

Т = Т, q ‘ + qд' = qа, где n - нормаль к плоскости сдвига D1E; q2Т,qд -плотности тепловых потоков в заготовку, Вт/м2;q2Т, qд - плотности тепловых потоков в АЗ, Вт/м2.

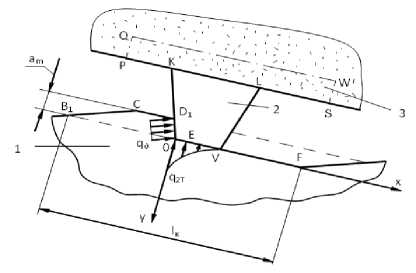
Рис. 1. Схема контакта пластически деформирующего АЗ с заготовкой:

1 - заготовка; 2 - АЗ; 3 - шлифовальный круг

Теплообмен на границах объектов, контактирующих со смазочно-охлаждающей жидкостью (СОЖ) или воздухом, задан в форме закона Ньютона-Рихмана, описывающего процесс конвективного теплообмена в виде

ат

^—А ■ Т =а^{( Т — Т} 0 )

, где Аz - коэффициент теплопроводности z-го объекта,

Вт / (м К); Т - температура z-го объекта, К; z - номер объекта (z = 1, 2, 3: заготовка, АЗ, шлифовальный круг соответственно); j - номер поверхности; a - коэффициент теплоотдачи от j-ой поверхности, Вт / (м2 К); n -нормаль к границе объекта. Зависимости для расчета скорости движения смазочно-охлаждающей жидкости (СОЖ) в зоне контакта шлифовального круга с заготовкой, расхода СОЖ через зону контакта и коэффициентов теплоотдачи от заготовки, абразивных зерен и связки круга к СОЖ приведены в [5, 7].

Невозможность априорного определения плотностей распределения тепловых потоков между контактирующими объектами, изменение положения зон тепловыделения во времени, необходимость учета зависимости теплофизических свойств контактирующих объектов и предела текучести материала заготовки от температуры создают трудности для аналитического решения дифференциальных уравнений. Задачу решали численным методом конечных элементов. Методика численного расчета на основе дискретных аналогов уравнений теплопроводности реализована в оригинальных программах.

Численное моделирование температур выполнили при следующих исходных данных: плоское многопроходное шлифование периферией круга; материал заготовки - сталь 40Х; материал АЗ шлифовального круга - электрокорунд нормальный; зернистость - F 60 (25-я); рабочая скорость круга V ; = 35 м/с; скорость продольной подачи V s пр = 10 м/мин; глубина шлифования t = 0,01 мм. Моделировали наложение на заготовку УЗК частотой 22000 Гц с различной амплитудой ( А у = 1 и 3 мкм) и фазой. Фиксировали локальные температуры Т 2 на площадке EV контакта зерна с заготовкой и Т 2' на площадке D 1 E в зоне пластического деформирования при диспергировании 21-м из последовательно работающих АЗ, когда материал заготовки прогрет в результате работы предыдущих зерен. При наложении колебаний амплитудой А у = 1 мкм, меньшей глубины внедрения пластически деформирующего АЗ в заготовку ( a m = 2 мкм), режим работы зерна не изменяется: на протяжении всего времени его контакта с заготовкой осуществляется пластическое деформирование. Локальная температура в зоне контакта АЗ с заготовкой (участок EV ) уменьшилась на 4%, а температура в зоне пластического деформирования (участок NE) - на 9% (рис. 2, 3).

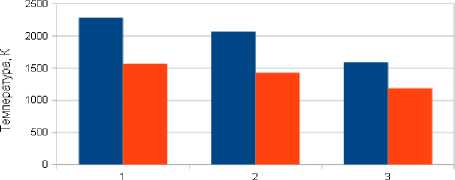
■ - в зоне контакта с заготовкой ■ - в зоне деформирования

Рис. 2. Температура в зоне контакта АЗ с заготовкой и в зоне пластического деформирования: 1 - А у = 0; 2 - А у = 1 мкм; 3 - А у = 3 мкм

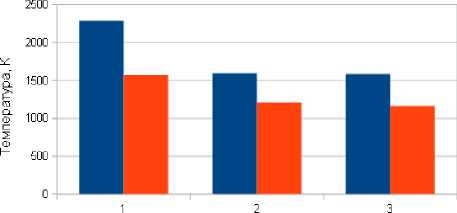
■ - в зоне контакта с заготовкой ■- в зоне деформирования

Рис. 3. Температура в зоне контакта АЗ с заготовкой и в зоне пластического деформирования: 1 - А у = 0; 2 - А у

= 3 мкм, ф = 0°; 3 - А у = 3 мкм, ф = 180°

Незначительное уменьшение температуры объясняется тем, что плотности тепловыделения в зоне пластического деформирования и в зоне трения АЗ о заготовку, определяющие температуры, практически не зависят от глубины внедрения зерна, которая изменяется при наложении УЗК. Поэтому снижение температур при малых амплитудах УЗК достигается не за счет изменения кинематики взаимодействия АЗ с заготовкой, а за счет изменения напряженно-деформирован-ного состояния в зоне обработки вследствие уменьшения предела текучести материала заготовки [6].

При наложении колебаний амплитудой А у =3 мкм, превышающей глубину внедрения АЗ в заготовку, режим работы зерна изменяется: на некоторое время АЗ выходит из контакта с заготовкой. При этом локальная температура в зоне контакта АЗ с заготовкой (участок EV ) уменьшается на 30%, а температура в зоне пластического деформирования (участок NE) - на 24% (см. рис. 2, 3). Меньшая температура зафиксирована при фазе колебаний ф = 180°. При этой фазе имеет место минимальная длина траектории, на которой АЗ осуществляет деформирование материала заготовки, что и обусловливает снижение теплосиловой напряженности процесса в большей степени (см. рис. 3). Для АЗ, осуществляющих пластическое деформирование, степень влияния фазы УЗК на локальные температуры ниже, чем для зерен, осуществляющих микрорезание [2].

При шлифовании без наложения УЗК локальные температуры увеличиваются с увеличением продолжительности контакта АЗ с заготовкой до момента времени 19,12-10⁶ с (кривые 1 на рис. 4, 5) и уменьшаются в конечный период времени контакта, когда деформируется слой материала, в меньшей степени прогретый в результате работы предыдущих зерен. При наложении колебаний с амплитудой А у = 3 мкм и фазой ф = 0° в начальный период контакта АЗ глубина его внедрения в заготовку выше, а в конце траектории ниже, чем в случае отсутствия УЗК, причем на некоторое время АЗ выходит из контакта с заготовкой. Соответственно и локальные температуры в начальный период контакта с заготовкой незначительно ниже, чем при шлифовании без наложения УЗК ( А у = 0) (кривые 1 и 2 на рис. 4, 5). На заключительном этапе контакта АЗ с заготовкой разность температур существенно выше, поскольку АЗ выходит из контакта с заготовкой. При фазе колебаний Ф = 180° в начальный период как глубина внедрения АЗ в заготовку, так и локальные температуры ниже, чем без наложения УЗК (кривые 3 на рис. 4, 5). На заключительном этапе глубина внедрения АЗ в заготовку при наложении УЗК увеличивается, поэтому увеличиваются и температуры, однако и на этом этапе температуры ниже, чем без наложения УЗК.

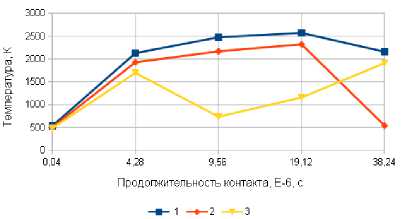
Рис. 4. Зависимость температуры Т 2 в зоне контакта АЗ с заготовкой от продолжительности контакта: 1 - А у = 0; 2 - А у = 3 мкм, ф = 0°; 3 - А у = 3 мкм, Ф=180°

Локальные температуры распределены на площадках контакта АЗ неравномерно. Например, в момент времени 19,12^10 6 с от начала контакта максимальное значение температуры в зоне контакта АЗ с заготовкой зафиксировано на расстоянии 15 мкм от вершины зерна (рис. 6); в зоне пластического деформирования максимальное значение температуры имеет место в середине этой зоны. Варьирование расходом СОЖ через зону контакта круга с заготовкой в пределах 25% привело к незначительному изменению локальных температур.

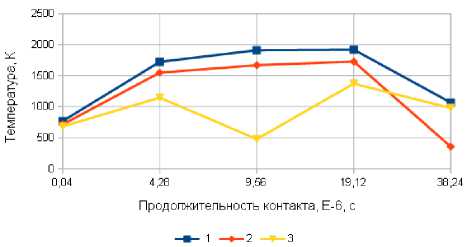
Рис. 5. Зависимость температуры Т 2^′ в зоне деформирования от продолжительности контакта: 1 – A y = 0;

2 – A y = 3 мкм, φ = 0°; 3 – A y = 3 мкм, φ = 180°

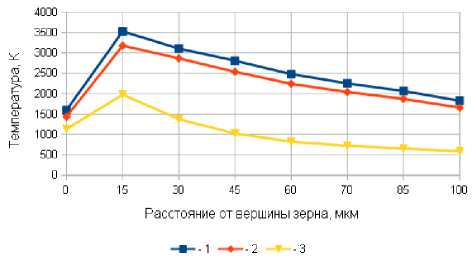
Рис. 6. Распределение температуры на площадке контакта пластически деформирующего АЗ с заготовкой: продолжительность контакта – 19,12·10^-6 с;

1 – A y = 0; 2 – A y = 3 мкм, φ = 0°; 3 – A y = 3 мкм, φ = 180°

Выводы: разработаны физические и мате матические модели для расчета температурного поля при шлифовании, позволяющие учесть изменение кинематики микрорезания пластически деформирую- щими абразивными зернами и механических характеристик материала заготовки при наложении УЗК. Приведены результаты численного моделирования локальных температур, показавшие, что наложение УЗК с амплитудой, большей глубины внедрения АЗ в заготовку, позволяет уменьшить локальные температуры на пластически деформирующих зернах на 24-30%. Установлено влияние амплитуды и фазы колебаний на локальные температуры, изменение температур в зависимости от времени контакта АЗ с заготовкой и распределение тем-ператур на площадках контакта зерна с заготовкой и стружкой.