Исследование магнитоанизотропных ключевых элементов для системы контроля тягового электродвигателя

Тел. (846) 995-54-13

лировочного винта 1, нажимных пластин 4, 5 и пружины 2. Нажимной элемент выполнен в виде набора сепараторов 7 с выступами, входящими в пазы 10 корпуса 3 для исключения продольного смещения, стальных шариков 6, которые помещены между магнитопроводами 8, 9.

Пластина 4 через пружину 2 связана с регулировочным винтом 1, устанавливающим её сжатие и определяющим величины усилия через шарики 6 на магнитопроводы 8, 9 и корпус 3. Под действием усилия в магнитопроводах возникают внутренние механические напряжения, которые фиксируют магнитные домены в определённом направлении и приводят магнитопроводы в начальное магнитное состояние, определяющее выключенное состояние ключа. При подаче напряжения на обмотку управления домены управляемых магнитопроводов меняют свое направление и остаются фиксированными с помощью

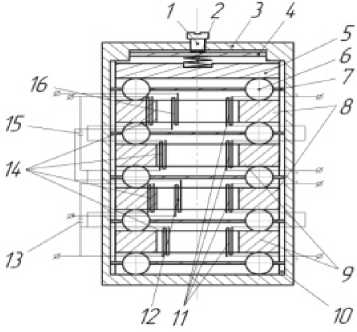
Рис. 1. Магнитоанизотропный ключевой элемент системы контроля ТЭД усилий, определяя включенное состояние. Выключенное состояние определяется подачей обратного напряжения на обмотку управления или его снятием [3].

Математическая модель МКЛ описывается уравнениями теории электромагнитного поля, ферромагнетизма и упругости. Решение этой модели в трехмерном пространстве связано с непреодолимыми трудностями. Поэтому задача реализации модели была сведена к двумерной. При этом управляемый магнитопровод заменяется эквивалентной пластиной в электромагнитном поле при силовом воздействии на нее, и вводятся следующие допущения [1].

• 1.    Магнитные индукции внешних электромагнитных полей, в которых находится пластина, изменяются по синусоидальному закону;

• 2.    Магнитные поля возбуждения и управления равномерны и имеют только нормальную составляющую магнитной индукции B z + B zo ;

• 3.    Комплексная магнитная проницаемость Ц_а напряженной магнитоанизотропной структуры (НМАС) пластины зависит от значений механических напряжений у силы P , и_п = f ( P ) ;

• 4.    Плотность токов ( ^ x ⁺ 5 xQ Х ^ , + 5 ур ) по толщине с пластины не изменяется, что имеет место при с/(2А) < 0,5 , где А - эквивалентная глубина проникновения электромагнитного поля в пластину;

• 5.    Тангенциальные составляющие напряженностей электрического поля ( E_a + E ao ) и ( E b + E bo ) на гранях пластины постоянны;

• 6.    Поля выпучивания, идущие в обход пластины, относятся к полям рассеивания;

• 7.    Механическая сила P (напряжение у ) направлена к магнитному полю ( B_z + B_z o ) в одной нормальной к пластине плоскости;

• 8.    Среда пластины анизотропна.

Физическая модель на рис. 2, с учетом принятых допущений в двухмерном пространстве при одновременном воздействии силового поля и полей возбуждения и управления описывает-

- -

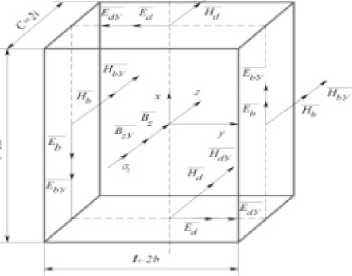
Рис. 2. Модель управляемого МКЛ при сжатии

H z ( y , x ) = 1 H b

^H zy ⁽ y , ^x ) = 1 ^H b

ся следующими дифференциальными уравнениями в декартовых координатах [1, 2]:

а ( я , + и ,у )

_д --- = Y x

5 у

» H + H zy ¹

5 x

= Y y E ⁺ E yy ) ;

⁵ E + E yy ) д ( E x + E y )

"Z=- = j(WH -OuJL ) ; (3)

5y ----

(®. B ) H ^H

V - z  -У 7 7

+

“  ' ; (4)

z^z 7

z

5v

E = о

5 z      z ’

где Y x , Y y , — электрические проводимости НМАС по соответствующим координатам x, y ;

Е_x, Е_у, Е_xУ, Е_уУ – напряженности электрических полей от обмоток возбуждения и управления соответственно по осям x , y ; Н_z, Н_zУ – напряженности магнитных полей от обмоток возбуждения и управления соответственно по оси z ; В_z, B_zУ – магнитные индукции обмоток от возбуждения и управления соответственно; ®=® У - круговые частоты полей возбуждения и управления; ст - нормальные механические напряжения в НМАС; Ц_а - магнитная проницаемость от механических напряжений о ; v - перемещение точки структуры по оси z .

Граничные условия при этом имеют вид:

H z ( У ) при x ± а ;

H z ( X , У ) =j H a 0

при x = ± а; у = 0; при у = ± b ;

' ^H zy ⁽ у ) при x ± ^а ;

^H zy ^{( x} , У ) =1 ^H a

при x = ± a; y = 0; при y = ± b ;

H z ( x ) при y = ± b ;

при y = ± b; x = 0; при x = ± а ;

' ^H z _y ⁽ x ) при y = ± b ;

при y = ± b; x = 0; (7) при x = ± а ;

0 при t <  t₁;

H zy ( x ) =

H ¹¹ z max

при t ₁ <  t <  t ₂ ;

при t >  t ₂ ;

0 при t <  t ₁ ;

H zy ⁽ У ) = 1 ^H z max     при t 1 <  t <  t 2 ;

0      при t >  1 ₂ ;

где a и b – размеры пластины; t – время срабатывания магнитоанизотропного ключевого элемента; t₁, t₂ – время включения и выключения магнитоанизотропного ключевого элемента (рис. 4)

Решение уравнения ферромагнетизма (4) в литературе известно и его решение имеет вид [1, 2]:

Mk -My = Мн-AM. + AMy -Мн + AM. = AM.- (9)

2,25 XaM2 p где А м = ——,5   '— - изменение магнит- г a            2 n 2 * 2 1

П B tj ной проницаемости НМАС, созданное механическим напряжением у усилия P; ДмУ – изменение магнитной проницаемости НМАС, созданное полем обмотки управления; Mi = BIH и находится по зависимости: в = f (H) – начальная магнитная проницаемость НМАС управляемого и компенсационного элементов от обмотки возбуждения; μУ и μк – магнитные проницаемости НМАС управляемого и компенсационного элементов; X - изотропная магнитострикция; a – коэффициент намагниченности; B – магнитная индукция ; tк и l – ширина и толщина кольца (пластины).

Совместное решение (2) - (4) дает

X_x , X_y , X_yy , X_xy - постоянные распространения электромагнитной волны в материал НМАС от силового поля, обмотки возбуждения и обмотки управления; А _x , А _y , А _xy , А y _y - эквивалентные глубины проникновения электромагнитного поля в материал НМАС от силового поля, обмотки возбуждения и обмотки управления; ψ =π/4 -β/2 – фазовый угол между индуктированной ЭДС и вихревым током; в - угол магнитных потерь.

Поскольку постоянные (11) есть величины комплексные, то решение уравнения (10) ищется в комплексном виде через круговые и гиперболические функции [1]

'^{( (} H z ⁺ H zy ^{)( x} , у ) ) = Ach ⁽X x ⁺ X xy ) ^x cos qy

( < H z ⁺ H zy ⁾⁽ у , ^x ) ) = ^B ch⁽X y ⁺ X yy ) y ^cos p^{x ; (12)}

Из условий (7) - (9) определяются постоянные А и В , которые подставляются в выражения (1.12), преобразуя их к виду

( ( H z + H zy ) ( x , y ) ) = ( H a + H ay ) ^C h^ ^{Z x + X xy} ) ^x cosqy ch^ X x ⁺ X xy ) a

( ( H z + H zy ) ( y , x ) ) = ( H b + H by ) c^{h X y + X yy} ) ^У cos px ; (13)

[---- ch^ y + X yy ) b

Третьи условия из (7) - (9) удовлетворяются при qb=pa=рn/2 .

((Hz + Hzy У a, У)) = Ё (b« + b»y ) C0S   ^ 3 X У n=1               2(b + by )

f ^{9 2 (} H z ⁺ H zy. ) )

l        x ² J

⁽ H z ⁺ H ) J l У ² J

( \        \     ^

Hz + Hzy Ab,x))=E(an i =1

⁺ a ny ^)C0S

n n

2( a + a_y )

;(14)

= ⁽ H z ⁽ x, y ⁾⁺ H zy ⁽ x, y ^{) )+(} H z ⁽ y , x ⁾⁺ H zy ( y , ^{x ) )}

;(10)

где a_n , a_nУ и b_n , b_nУ коэффициенты Фурье ( n =1, 3, 5…), определяемые формулами [1]

где

(Xx + Xxy ) = ^ Y (M. + My) = (А J ) ej

( X y ⁺ X yy ) = V N, ⁽M. ⁺ M y ) = ( _А + ¹ _А ) e j

^{( a} n ^{+ a} ny ) =

2( a + a_y )

f 4(H^'J l   nn J

+ ( a + a y )

J ( H z + H zy ) ( b , x )

- ( a + a y )

n nx cos

2( a + a_y )

( bn + b y ) =

. nn sin—

+ ( b + b y )

-----   ( H + H ) (aa, y )cos——— 2( b + by ) . ( 2 b y ^z^^LV "  2( b + by )

( А x +А xy ) = ,      ,¹        .

v    (M. + My )

^(а y ^{+ А} yy ) = I •    (        \

J®/( (M. + My )

f 4(H^ J l nn J

. nn sin

Из выражений (12) - (15) окончательно находятся значения

( ( H z + H zy ) ( x , y ) ) = ( H a + H ay ) ch ( ^{X x + X} ) x Ф п ( y )

-- --- --- ---- ^{ch (} X x ⁺ X x, ) a

( ( H z + H zy ) ( y , x ) ) = ( H b + H by ) ch ^{(( X y + Х} / У Ф п ( x ) ;(16)

— --- — --- ch (Xy + Xy,)b и тогда уравнение (10) принимает вид

Единичные функции (20), представляющие граничные условия, существенного влияния на результаты анализа не оказывают [2] и могут быть положены Ф _п ( x ) = Ф _п ( y ) = 1 .

Вихревые токи в эквивалентном контуре L y = 2( t y + l y ) НМАС находятся путем интегрирования выражений (18):

( H z + H zy ) = ( H a + H ay ) ch ^^^^. ф п (y ) + — --- — --- ch ⁽ X x ⁺ X x, ) a

, И A ch ⁽ X y ⁺ X yy ) y   , .

^{+ ( H} b ⁺ H by )     --- y—T Ф п ^{( x} )

--- ---- ch ⁽ X y ⁺ X yy ) ^b

⁽ a + a y )

+ U ) = c J ( £ y + S y, ) dx =

c ⁽ E a ^{+ E}a, )   cha - 1

P ⁽ X + X , ) sh ⁽ X + X , 'a

^{( b + b} , )

+ Ij bY ) = c J ( S x + S x, ) dy =

^{c (} E b ^{+ E}b , ¹ chb - 1 . p ( x + X , ) sh ( X + X , ) b’

а уравнения (2), (3)принимают вид для плотно стей токов ⁵ + 5 xy ) и ⁽ f y ⁺ 5 yy ) :

Сопротивления НМАС вихревым токам определяются с учетом выражений (19), (21), (22):

_s     l ^{d H (} y ’ ^x ) z ^{+ H (} y ’ ^x ) zy ) )

^{5 + 5} ) =V         _{d y}         7

sh ( X y ⁺ X yy ) y   . _A

= -Y x E ⁺ E by iV---. Ф п ^{( x} ) sh ( X + X ) b

⁽ Z tB ⁺ Z B У ) = Э t / ( I B ^{+ 1} tB y ) = /     э \^p e^{y >}'

^{c ( a} E ^{+ a} E У )

⁽ Z IB ⁺ Z B У ) = ^ЭI / ( I B ^{+ 1} IB У ) =

t-э p e^j' ^ ; c ^{( b}E ^{+ b} E У )

S y + ⁶ уу

) p⁽ H ^{( x} , y ) _z + H ^{( x} , y ) _zy ) ' ²                5 x             ,

(23) полное сопротивление вихревому току запишется как сумма выражений (23)

V

= -у , (e„ + E a, ) sh ^{( X x + X xy} ) •^x Ф п ( y )

— --- sh ( X x + X xy ) a

= ;(18)

( Z B + Z b, ) = 2 p l^ ². e j ^ a V c ( ^aE ^{+ a}E, )

/

+______12______ e j ^ b

c ^{( b}E ^{+ b}E, )

где

⁽ E L ⁺ E a, ) =^{- (} P y X x ⁽ H a ⁺ H ay ^{) h} X x^a ) =^- j to V B^ + B ay ) a B

( E + E by ) = - ( p x X y ( H b + H by ) h X b ) = - j m ( B b + B by ) a_B ^;(19)

(24) где с – удельное электрическое сопротивление НМАС МКЛ; t_э , l_э – стороны эквивалентного контура вихревых токов; a_Е , b_Е , a_ЕУ , b_ЕУ – эквивалентные глубины проникновения электрического поля в НМАС от силового поля и обмоток возбуждения и управления, соответственно; с – средняя длина пути магнитного потока,

.        4      1 - пп пnx ф.(x) = —L   '"'  .cos — п 7Г । п 2       2 a

4     1 . п п       п пу

Ф п ⁽ y ) = —L —^sm 7-^cos tit;    (20)

п 7~ 1 п 2         2 b ’ ^{v z}

B _a , B_b , B_aУ , B_bУ – комплексы действующих индукций в НМАС от обмотки возбуждения и от обмотки управления, равномерно распределенных на эквивалентных глубинах a_B и b_B , которые позволяют найти участки l_э и t_э эквивалентного контура L_э вихревых токов.

В эквивалентном контуре НМАС действует ЭДС

V a , V b , V a, , V by - углы сдвига между вихревым током и ЭДС по соответствующим направлениям эквивалентного контура НМАС от обмоток возбуждения и управления, соответственно.

Эквивалентные глубины проникновения электрического поля в НМАС определяются с учетом выражений (11)

⁽ a E

⁺ a E У

) = b + b_{E у}== -

E    E У     k

chK 1

chK 1

- cos K ₂

+ cos K ₂

;(25)

Э = Э + 3 y , (21) где Э = 2 ⁽ E_at э + Е_ь1_э ) = - ]шф - ЭДС от обмотки возбуждения;

^Эу = ²( E_a y t э ^{+ E} by ¹ э ) = ^- ,1 ^{а ф}у - ЭДС от обмотки управления.

где

K = a I A = a xjту ( ц_а + p , ) ;

K 1 = K cos(п 14 - вI2);(26)

K ₂ = K sin( п 14 - в 12) ;

у = 1I p = у cos у - jy sin у ;(27)

R -       ^B m ^H c ^(pi - ^P- )

в = arcsin ----———---- - угол магнит-

16 пВ ных потерь[1; 2],

B_m – магнитная индукция; H_c – коэрцитивная сила.

Углы сдвига между вихревым током и ЭДС.

cos y _а = cos y b

K 1 shK 1 + K 2 sin K 2

K-^sh² K 1 + sin² K ₂

При отсутствии поверхностного эффекта, что имеет место при K = а^ ю ( ц_д + ц _у ) у <  0,5 , эквивалентные глубины проникновения электрического и магнитного полей равны ( Ь_в + Ь_ву ) = Ь ;

sin Уa = sin Уь

K ₂ shK 1 + K 1 sin K ₂ ; (28) ky/sh² k 1 + sin ² k ₂

Сопротивления НМАС магнитопровода намагничивающему току от силового поля и обмоток возбуждения и управления 1_ф = c H по со-

^{( а} в ^{+ а} ву ) a , ^{( Ь}Е ^{+ Ь}Еу ) ⁽ a E ^{+ а}Еу ) 0-^{5( а}в ^{+ а}ву ) , а магнитная индукция распределяется равномерно по сечению элемента в с = в ( а в + а ву )/ а [1]. При этом можно пренебречь составляющими, пропорциональным круговым функциям в выражениях (1.28) (1.32). Тогда

ответствующим направлениям эквивалентного контура определяются с учетом выражений (19) и (21)

(7  .7  \   ^Э В( ^(Цд ⁺ Цу ) ^e

\ ^ZtФ ^{+ Z} tФФ =          с

К ™Ч^Ь в (М д ⁺ М у ) e^ ’ ⁽²⁹⁾ \ ^Z № ^{+ Z} lФФ =        с

cos y = sin a = K ₂ / K = sin( ^ /4 - в /2)

cos a = sin y = K 1 / K = cos( n /2 - y ) ^{; (33)}

С учетом изложенного, сопротивление вихревому току (25) НМАС магнитопровода, приведенное к виткам соответствующей обмотки, приобретает вид:

⁽ Zb ⁺ Z hV ) = ^p

а полное сопротивление НМАС магнитопровода намагничивающему току от силового поля, обмоток возбуждения и управления запишется как сумма выражений (29)

7 + Z . 2 ^НЦ с ^Ц ) ( t , ( a_B + a_B y e + l , ( Ь в + Ь_В у e ) ;(30) где a_b , b_b , a_bУ , b_bУ – эквивалентные глубины проникновения магнитного поля в НМАС от обмотки возбуждения и обмотки управления; ц у , ц_у -магнитные проницаемости пластины от механического усилия и поля управления; a a , a b , а_аУ ьу_ьу – углы сдвига между намагничивающим током и магнитным потоком по соответствующим направлениям эквивалентного контура от силового поля и обмоток возбуждения и управления соответственно.

Эквивалентные глубины проникновения магнитного поля определяются с учетом выражений (11)

L э c ^{( а} Е ^{+ а} Еу )

k 2 e^j

где L , = t + 1 - длина эквивалентного контура вихревых токов; t=2b , l=2a – ширина и толщина пластины; k_п – w/w_У коэффициент приведения сопротивления управляемого элемента к соответствующей обмотке w .

Активная и индуктивная составляющие сопротивления вихревому току равны

^{( г} в ^{+ г} ву ) = ^{( Z} в ^{+ Z} ву ^{) cos y}

^{( х} в ^{+ х} ву ) = ^{( Z} в ^{+ Z} BУ ^{) sin y}

( 2 ф ^{+ Z} ФУ ) = ^to( S ³ + S ^эу ) ⁽ Ц д ⁺ Ц у ) ^k„² e^{j a} ; (36)

где ⁽ S з + S ,у ) =⁽ S + ^S у ) = L , ^{( а} в ^{+ а} ву ) = tl при

отсутствии поверхностного эффекта. Активная и индуктивная составляющая Z_Ф .

/         \ т \ n chK 1 - cos K ₂

⁽ а в + ^а ву ) = ^{( Ь} в ^{+ Ь}ву ) = у J“тт; ■         ;(31)

k \ chK 1 + cos K ₂ ^{Л 7}

( Г ф + Г фу ) = ( Z Ф + Z фу ) sin a

^{( Х} ф ⁺ x-фу ) = ⁽ Z ф ^{+ Z} ФУ ^{) cos a}

;     (37)

где К , К₁ и К₂ – определяются по (25) - (27)

⁽ М д ⁺ Ц у ) = ⁽ М д ⁺ Ц у ) cos a ^- j⁽ М д ⁺ Ц у ) sin ^a .

ЭДС эквивалентного контура, приведенная к первичным виткам

Э = to B_cS ₃ w 1 ;            (38)

Углы сдвига между намагничивающим током и магнитным потоком

cos a a

K.sh 2 K , + K, sin 2 K, = cos a _в = — 1,   ¹²    =

K-^sh ² 2 K 1 + sin ² 2 K ₂

Так как сопротивления вихревым и намагничивающим токам расположены параллельно друг другу, то комплекс полного результирующего сопротивления НМАС магнитопровода определяется [1]:

sin a = sin a aB

K ₂ sh 2 K 1 + K 1 sin 2 K ₂ ; (32) k^sh ² 2 k 1 + sin² 2 k ₂

^{( z}p + ²ру ) =

^{( z} ь ⁺ Z ьу ^(2 ф + 2 фу ) (( Z ^ + 2^7 ) +( | Ф + 2 Фу ))’ <³⁹>

По аналогии определяются активная и реак- тивная составляющие (Zp + Zp, ).

При отсутствии поверхностного эффекта ( К < 0,5 ), что имеет место для НМАС из магнитомягкого феррита, глубины проникновения поля управляемого элемента и его сопротивление вихревому току от обмотки возбуждения и обмотки управления Z_b и Z_bУ практически не зависят от механических напряжений у силы P . Сопротивление же намагничивающему току Z_Ф и Z_ФУ изменяется при действии напряжений у и выражение (36), в зависимости от бокового сжатия НМАС кольцевого магнитопровода с учетом выражений (9) приобретает соответствующий вид [1, 2]:

® ( S₃ + S_{3 y}) f    2,25 Я_$аЦ P

⁽ 2 ф ⁺ 2 фу )= э ——I Ц-- 2 „2^ н ⁺ Ц , кe ;(40)

— --- с V п B t l J

По найденным значениям Z_р находится на-

Uw пряженность магнитного поля H = —1—L и да-Zpl лее по кривой намагничивания B = f (H) находится B и начальная магнитная проницаемость Ц. = B / H , где U1 - напряжение питания преобразователя.

Для магнитной цепи конструкции МКЛ на рис. 2 составляется схема замещения, которая представлена на рис. 3.

Для схемы замещения по 2-му закону Кирхгофа составляется система уравнений[1]

'и, + U * - U. = U 1 + U , K

'u, - u, - Uz = о         •    <41> вателя; KУ – коэффициент трансформации обмотки управления.

После перехода к магнитным индукциям система уравнений (41) принимает вид:

' B y + B k - B c = B 1 + B y

\ B y - B k - B = 0      •     ⁽⁴²⁾

где B_y , B_k - магнитные индукции в сердечниках управляемого и компенсационного элемента; B_c – магнитная индукция в сердечниках элементов за счет напряжения на конденсаторе; B₁ – магнитная индукция в сердечниках элементов за счет напряжения питания U 1 ; B_z - магнитная индукция в сердечниках элементов за счет напряжения на нагрузке.

Выражения для магнитных индукций запишем в виде

B_v = ( Н. + Н Ц_у ; B = ( н. - Н ) ц У 1     2 У к 1     2 к

U      2 Hc     U_yK

B 1 = ^^ ; B c = 2— 2 ; B_y = ^-^ ,   ⁽⁴³⁾

® Sw₁ — 2 SCw^ — oSw 1

где ^ 1 - напряженность магнитного поля, со здаваемая в сердечниках управляемого и компенсационного элемента за счет протекания тока в первичной цепи преобразователя; ^ 2 - на пряженность магнитного поля, создаваемая в сердечниках элементов за счет протекания тока во вторичной (измерительной) цепи преобразователя; НУ – напряженность магнитного поля, где Uy, Uk, Uc, Uz – соответствующие напряжения на обмотках управляемого и компенсационного элемента, контурном конденсаторе С и нагрузке Z; U1 - напряжение питания преобразо-

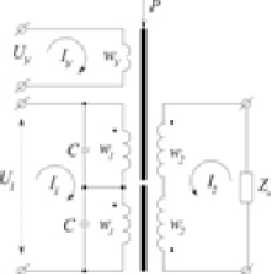
Рис. 3. Схема замещения магнитоанизотропного ключа

создаваемая обмоткой управления; ЦУ и Цк - комплексные магнитные проницаемости управляемого и компенсационного элемента[1]; w1 и w2 – число витков обмоток возбуждения и измерительной; S – сечение магнитопроводов силоизмерительных элементов; KУ – коэффициент трансформации обмоток w1 и wУ.

После подстановки (43) в систему уравнений (42) она преобразуется к виду:

( ^H 1 ^{+ H} y ) ^Ц У ⁺ ^ ^Ц У ^{+ Ц} к V

+ ( H ₂ + H_y )Ц^у_у + А д _У -s

( H ₁ + H_y ) ( ц _у + Ац _у -

2 c )

^² SCw - _v

oSw1 ц, )+

^{+ ( H} 2 ⁺ H y ) Ц у ^{+Ц +} Ц к

V

+

U 1 ₊ U y K y

m Sw₁

;(44)

cZ ^^

d S^W₂ J

= о

Решением системы уравнений (42) находится напряженность магнитного поля H ₂ :

H

₌ ( U ₁ + U _У K _У )( µ _У + Δ µ _У

2 ⁼

2 c ²

- µ _k ) ω Cw ₁ ² K_{T ;(45)}

где K_T = ² – коэффициент трансформации w ₁

обмоток w₂ и w₁ .

Выходное напряжение, снимаемое с Z_н , записывается выражением

U í = I 2 Z í

H 2 c

Z_í w 2      ,

которое после подстановки в него выражения (1.45) приобретает вид:

( U ₁ + U _У K _У )( µ_У + Δ µ_У - µ_k ) ω Cw ₁ U н ⁼

2 c

¹ Z н ;(47)

V 2 J _s Δ H ₂       0,89 π ² B ² t ² lU _У

⁼    β ^{'    =} λ Cβα ² µ ² PK ω Sw ^{. (50)}

sн з

Скорость смещения доменных границ определяется с учетом (1.50) выражением [1]

t = Δс = λsCαs2µн2PKзωУSwУ ср V       0,89π2B2t2lUУ    ;    (51)

где β ^' = 2 πµ ₀ λ _p γ / 2 υ ² A – коэффициент затухания движения границ доменов [1]; λ _p – релаксационная частота; γ – плотность граничной энергии; υ – магнитомеханическое отношение; А – обменный параметр; µ ₀ – магнитная постоянная. Время срабатывания ключа определяется временем установки доменов под действием магнитного поля Δ H ₂ , т.е. временем удлинения магнитопровода ключа Δ c под действием Δ H ₂ и определяется с учетом (51) выражением:

На выходе обмоток 11 появляется максимальный сигнал, который на Z_н определяется выражением (47) с учетом выражений (9) и имеет вид:

t ₌ Δ с ₌ λ _sC α _s ² µ _н ² PK_з ω _УSw_У ^{ср =} V ⁼   0,89 π ² B ² t ² lU _У    ^;

U н

1,125( U ₁ + U_У K_У ) λ _s α _s µ _н ω w ₁ P π ² B ² t ² lc

Исходя из равенства потерь в магнитопроводе и обмотках ключа можно приближенно определить максимальную коммутируемую мощность:

Z н , (48)

Из выражения (47) видно, что для перевода ключевого элемента во включенное состояние необходимо, чтобы Δ µ _у ≥Δ µ . Это условие позволяет определить величину напряжения, приложенного к обмотке управления:

Q k . max

fB s Q a S ²10¹²

1,5 δ G    ^;

U _У = К _з Δ µ _У H ₂ ω _У Sw _У ,      (49)

где ω_у – круговая частота управляющего напряжения; w_у – число витков обмотки управления; К_з =1,3 – коэффициент запаса, обеспечивающий надежное срабатывание ключа.

При выключении МКЛ U_У=0 все вышеприведенные выражения упрощаются и параметры связанные с этой обмоткой становятся равными нулю, фиксируя выключенное состояние.

Изменение магнитного поля ΔН под действием напряжения на обмотке управления U_У находится из выражения (49), которое после подстановки в него выражения (9) принимает вид:

где f – частота; B_s – индукция насыщения магнитопровода; Q_a – потери в магнитопроводе; S – сечение магнитопровода; G – вес магнитопровода; δ – плотность тока в обмотке.

Разработанная методика была использована для расчета МКЛ на ферритовых кольцах 10 П б П 4,5 мм марки 2000 НМ1 при следующих исходных данных: U₁ =4,5 B; f = f_У =40 кГц; U_У =0,8 В; P_max =50 Н; w₁ = w_У =50; w₂ =100; С =50 пФ.

Используя выражение (48) для данного МКЛ построена расчетная выходная статическая

характеристика U_н = f ( U_У ) , которая представлена на рис. 4 совместно с экспериментальной зависимостью.

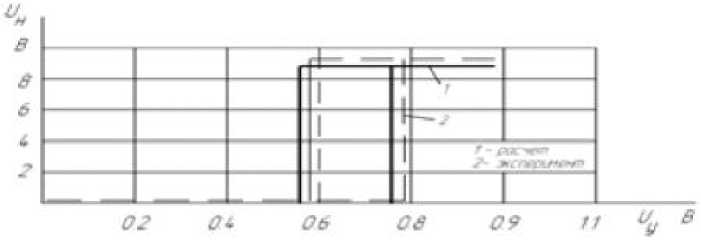
Рис. 4. Выходная статическая характеристика МКЛ U = f ( U_У )

Параметры включения и выключения на рис. 4 отличаются друг от друга вследствие внутренней вязкости феррита, т. е. наличия гистерезиса.

В результате теоретических и экспериментальных исследований установлено, что сходимость выходных характеристик не превышает 5%.