Исследование магнитооптических резонансов в диэлектрических дифракционных решётках на основе анализа дисперсии и структуры собственных мод

Изучение взаимодействия света с периодическими металлодиэлектрическими структурами является предметом интенсивных исследований. В таких структурах существует широкий круг экстраординарных (резонансных) оптических эффектов, включающих экстраординарное пропускание, полное поглощение падающего излучения, резонансное изменение спектров прохождения и отражения на определённых частотах, формирование областей с высокой степенью локализации энергии вследствие интерференции затухающих и плазмонных волн [1–6].

Особый интерес представляют дифракционные структуры, содержащие намагниченные материалы . В таких структурах возникают новые, магнитооптические эффекты, связанные с преобразованием поляризации света и резонансным изменением спектров отражения и пропускания при изменении намагниченности [7–12]. В работах [11, 12] рассмотрены структуры, состоящие из металлической дифракционной решётки и намагниченного диэлектрического слоя. В этих работах показана связь магнитооптических резонансов с возбуждением дифракционной решёткой квазиволноводных мод в намагниченном слое. При использовании металлической дифракционной решётки магнитооптические резонансы существуют только при TM-поляризации падающей волны. Кроме того, для описания резонансов в [11, 12] были использованы дисперсионные соотношения для мод плоскопараллельного волновода. Применение таких соотношений возможно только при выполнении след ующих условий. Во-первых, размер щелей решётки относительно величины периода должен быть малым (порядка 10%). Во-вторых, толщина металлической решётки должна быть значительно больше, чем толщина скин-слоя. В этом случае при анализе мод структуры можно заменить дифракционную решётку бесконечным металлическим слоем и рассматривать структуру как диэлектрический волновод с металлической обкладкой.

При рассмотрении структур, содержащих металлическую дифракционную решётку с большим относительным размером щелей или диэлектрическую решётку, такой подход, как правило, оказывается несостоятельным. В этом случае моды структуры могут локализоваться не только в диэлектрическом слое, но и в дифракционной решётке. Для точного расчёта дисперсионных зависимостей мод структуры в этом случае используется подход, основанный на расчёте полюсов матрицы рассеяния [13–18].

В настоящей работе исслед уются магнитооптические резонансы диэлектрической дифракционной структуры, состоящей из н амагниченных в плоскости дифракционной решётки и однородного слоя. На основе численного моделирования показано, что в таких структурах существуют магнитооптические эффекты, состоящие в резонансном изменении пропускания и отражения при изменении намагниченности. В отличие от рассмотренных ранее структур, резонансны е эффекты существуют для обоих типов поляризации падающей волны (ТЕ и ТМ). Для объяснения резонансов проведен расчёт и анализ дис- персионных зависимостей, основанный на расчёт е полюсов матрицы рассеяния. На основе анализа дисперсионных кривых, структуры мод и условий их возбуждения предложена классификация возникающих резонансов.

Геометрия структуры и магнитооптические эффекты

На рис. 1 представлена геометрия исслед уемой структуры и её параметры. Структура состоит из бинарной диэлектрической дифракционной решётки и однородного диэлектрического слоя.

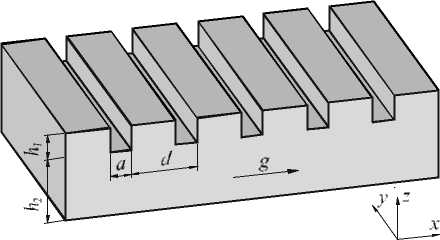
Рис. 1. Геометрия структуры (период d = 1100 нм , высота решётки h 1 = 135 нм, высота слоя h 2 = 960 нм , ширина отверстий решётки a = d / 4 = 240 нм )

Структура предполагается выполненной из намагниченного материала, вектор намагниченности направлен вдоль оси Ox , перпендикулярно штрихам решётки. В этом случае диэлектрическая проницаемость материала структуры имеет вид [19, 20]:

е 0 0

^Е = 0 ^е ig

0 - ig где g — модуль вектора гирации среды, пропорциональный намагниченности. В работе структура предполагается выполненной из распространённого материала магнитооптики Bi2.2Dy0.8Fe5O12 (висмутзамещённый диспрозиевый феррит гранат) [20]. В области ближнего ИК (в окрестности %= 1200 нм , ®~ 1,57-1015 Гц) параметры тензора (1) для данного материала принимают следующие значения: е = 5,06 + 4,3 -10-4i, g = 0,015- 3 -10-5i.

Расчётные спектры пропускания рассматриваемой структуры представлены на рис. 2. Все пред-ставленны е в работе расчётные зависимости получены на основе строгого решения задачи дифракции по методу Фурье-мод [21–23]. На графиках TE- и TM-спектров виден ряд резонансов. Для удобства дальнейшего рассмотрения резонансы обозначены TE TE TE TM TM TM как A ,B ,C ,A ,B ,C . Под величиной магнитооптического эффекта I понимается изменение коэффициента пропускания T (интенсивности нулевого прошедшего порядка дифракции) структуры при её намагничивании [20]:

I = T ( g ) - T ( 0 ) .                                  (2)

Соответственно, наибольшая величина эффекта (2) будет наблюдаться именно в окрестностях указанных резонансов. Спектры величины магнитооптических эффектов показаны в нижней части рис. 2.

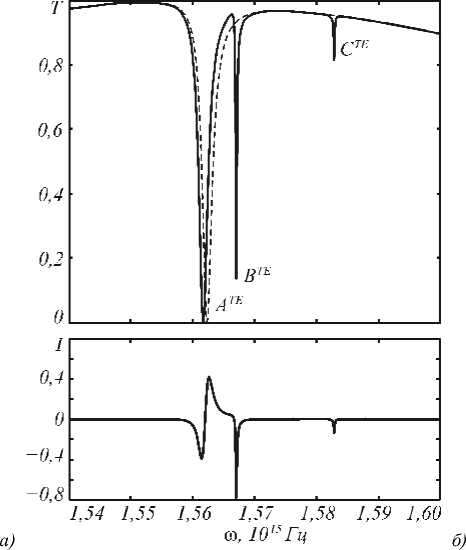
Рис. 2. Спектры пропускания T (сверху) и величины магнитооптических эффектов I (снизу) при нормальном падении волны с TE-поляризацией (а) и TM-поляризацией (б) (спектры пропускания намагниченной структуры — непрерывная линия, ненамагниченной структуры — пунктирная линия)

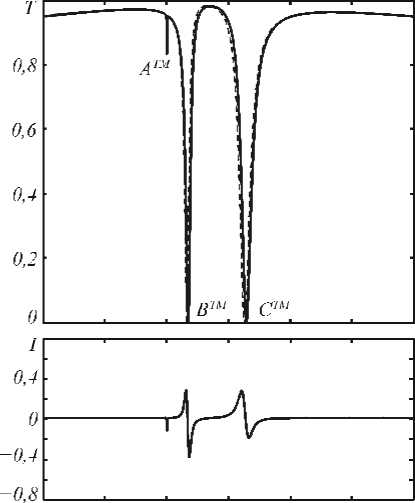
1.54 1.55 1.56 1.57 1,58 1,59 1,60 to, IO¹'Гц

Для ТЕ-поляризации падающей волны изменение пропускания достигает 80% (резонанс B ^TE ), а для ТМ-поляризации — 30% (резонанс B ^TM ). Отметим, что аналогичные резонансы и аналогичные по величине магнитооптические эффекты присутствуют и в спектре отражения структуры.

Магнитооптические эффекты (резонансы) на рис. 2 можно условно отнести к двум типам. Эффекты 1-го типа обусловлены смещением резонансных минимумов (максимумов), наблюдаемых в спектре намагниченной структуры относительно спектра ненамагниченной структуры. Такими являются ре- TM зонанс A ^TE в TE-спектре и резонансы B ^TM , C ^TM в TM-спектре рассматриваемой структуры. Эффекты 2-го типа заключаются в возникновении при намагничивании новых резонансов, отсутствующих в спектре ненамагниченной структуры . Такими в рассматриваемой структуре являются резонансы B ^TE и C ^TE в TE-спектре и резонанс A ^TM в TM-спектре.

Анализ дисперсионных кривых

Как правило, резонансные изменения спектров пропускания и отражения связаны с возбуждением собственных мод структуры [2–5, 16–18]. Для объяснения резонансов на рис. 2 в работе был проведён расчёт дисперсионных кривых мод структуры, основанный на вычислении полюсов матрицы рассеяния. Для полноты изложения приведем определение матрицы рассеяния и описание расчётного метода. При решении задачи дифракции света на периодической дифракционной структуре по методу Фурье-мод вычисление комплексных амплитуд порядков дифракции сводится к решению системы линейных алгебраических уравнений [13–15]:

S - 1

R

T

I

I '

где R и T — векторы комплексных амплитуд отражённых и прошедших порядков дифракции, а I и I ' — векторы комплексных амплитуд волн, падаю- щих на структуру сверху и снизу, соответственно. Предполагается, что направления падающих волн согласованы с направлениями дифракционных порядков. Матрица S в (3) называется матрицей рассеяния. Матрица рассеяния определяется геометрией структуры, оптическими свойствами материалов и параметрами падающего излучения [13–18]. Однородная система уравнений

S - 1

R

T

= 0

описывает моды структуры . При фиксированной геометрии структуры матрица S является функцией частоты to и константы распространения k_x : S = S ( to , k x ) . Построение дисперсионных зависимостей k x = k x ( to ) основано на решении дисперсионного уравнения

1/det S ( to , k_x ) = 0. (5)

Таким образом, при фиксированной константе распространения моды, частоты являю тся полю -сами матрицы рассеяния S [13–15]. В д анной работе константа распространения рассматрив ается как действительная ф унк ция комплексной частоты [15]. При этом строится аналитич еско е продолжение S = S ( to , k x ) как функции от to . Отметим, что при по стро ении аналитического продолжения, функция S ( to , k x ) получается многозначной [13]. Практический интерес представляют толь ко решения уравнения (5), обладающие мало й мнимой частью to (то есть находящиеся в окрестности прямой Im to = 0). Для получения таких решений в большинстве случ аев достаточно рассматривать однозначную функцию S ( to , k x ) , являющую ся аналитической в окрестности прямо й Im to = 0 [13]. Распределение поля, соответствующее рассматриваемой моде, определя ется из решения од нород ной системы (4).

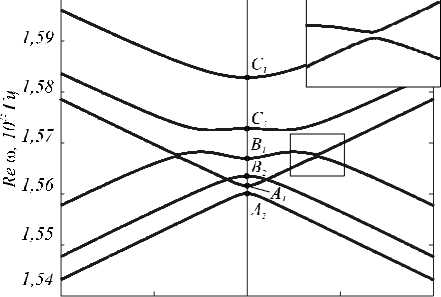
На рис. 3, 4 представлены рассчитанны е дисперсионные кривые для ненамагниченной ( g = 0 в (1)) и намагниченной структур, соответственно. Кривые получены численным решением уравнения (5). Каждая кривая на рис. 3, 4 описывает мод у. Точками A i , B i , C i , i = 1, 2 на рис. 4 отмечены пересечения дисперсионных кривых с прямой k_x = 0 . Ординаты отмеченных точек соответствуют частотам, при которых моды могут возбудиться при нормальном падении света на структуру. Отметим, что дальнейшее исследование резонансов проводится при нормальном падении и при малых углах падения. Поэтому дисперсионные кривые на рис. 3, 4 приведены не во всей первой зоне Бриллюэна k_x е [ -л / d , п / d ] , а только в центральной её части .

Сравнивая дисперсионные кривые на рис. 3 и 4, можно отметить следующую интересную особенность. Естественно предположить, что при малых значениях g дисперсионные кривые мод намагниченной структуры будут близки либо к законам дисперсии TE-мод, либо к законам дисперсии ТМ-мод ненамагниченной структуры. Действительно, дисперсионные кривые на рис. 3, 4 близки по форме и только несколько смещены по частоте (величины смещения резонансов Ai, Bi , Ci, i = 1, 2 и их частоты и длины волн приведены в таблице 1). В работах [11, 12] говорилось о модах ТЕ- и ТМ- типов намагниченной структуры в предположении близости их законов дисперсии к модам ненамагниченной структуры. В то же время, как показывает рис. 4, данное предположение не всегда выполняется. На дисперсионных кривых для рассматриваемой намагниченной структуры возникло расщепление мод (увеличенный фрагмент на рис. 4). На рис. 3 кривые ТЕ- и ТМ-мод ненамагниченной структуры пересекаются в окрестности kx = ±0,02п / d . При намагничивании данные кривые расщепляются в окрестности точки пересечения и образуют моды намагниченной структуры. Таким образом, дисперсионные кривые мод намагниченной структуры могут одновременно содержать фрагменты, соответствующие кривым TE- и TM-мод ненамагниченной структуры. При ув еличении g указанные расщепления начинают проявляться и для кривых мод, содержащих точки

A 1 , B ₂ в окрестности k x = ± 0,005 п / d . О модах TE-и TM-типов в намагниченной структуре можно говорить лишь в пределах некоторых интервалов. В окрестности прямой k x = 0 дисперсионные кривые, содержащие точки A ₁ , A ₂ , представляют моды ТЕ-типа. Соответственно дисперсионные кривые, содержащие точки В ₁ , В ₂ , C ₁ , C ₂ представляют в окрестности прямой k x = 0 моды ТМ-типа.

Рис. 4. Дисперсионные кривые мод намагниченной структуры. Увеличенный фрагмент показывает расщепление дисперсионных кривых мод TE- и TM-типа

Таблица 1. Частота, эквивалентная длина волны и величина смещения резонансов

	A 1	A 2	B 1	B 2	C 1	C 2
Re ® ( 0 ) ,1015 Гц	1,5622	1,5606	1,5665	1,5633	1,5827	1,5725
Re Х ( 0 ) , нм	1205,77	1207,00	1202,46	1204,92	1190,15	1197,87
Re Х ( g ) - Re Х ( 0 ) ,нм	–0,46	–0,39	0,40	0,16	0,08	0,25

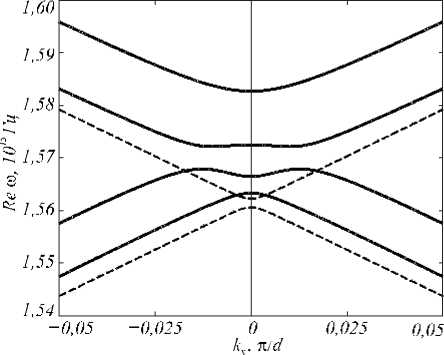
Рис. 3. Дисперсионные кривые мод ненамагниченной структуры (пунктирные линии — TE-моды; непрерывные линии — TM-моды)

1,60

-0,05    -0,025       0        0,025      0,05

к,, TUd

Вернёмся к рассмотрению резонансов на рис. 2. которых тип поляризации совпадает с поляризацией Для этого сравним положения магнитооптических падающей волны. Указанные резонансы вызваны резонансов, отмеченных буквами на рис. 2, c точка- смещением дисперсионных кривых вследствие на- ми Ai, Bi, Ci, i = 1,2 на дисперсионных кривых намагниченной структуры на рис. 4. Для случая падения волны с TE-поляризацией получим следующее соответствие:

A ^TE ^ A 1 ; B ^TE ^ B 1 ; C ^TE ^ C 1 .              (6)

Для волны с TM-поляризацией соответствие имеет вид:

A ™ ^ A 2 ; B ™ ^ B 2 ; C ™ ^ C ₂.         (7)

Соответствия (6), (7) выполняются с большой точностью: расстояние межд у магнитооптическими резонансами на рис . 2 и точками дисперсионных кривых на рис. 4 по длине волны не превосходят 0,1 нм.

Соответствия ATE ^ A1 в (6) и B™ ^ B2, C™ ^ C2 в (7) показывают, что магнитооптические резонансы первого типа на рис. 2, заключающиеся в смещении резонансов при изменении намагниченности, обусловлены возбуждением мод структуры, у магничивания.

Соответствия B ^TE ^ B 1 , C ^TE ^ C 1 в (6) и A ™ ^ A ₂ в (7) показывают, что магнитооптические резонансы второго типа обусловлены возбуждением мод с поляризацией отличной от поляризации падающей волны. Отметим, что частный случай резонансов второго типа был рассмотрен в работах [11, 12], где исследовались квазиволноводные TE-моды, возбуждаемые падающей волной с TM-поляризацией.

Симметрия мод при нормальном падении света

Соответствиями (6) и (7) объяснены все резонансы на рис. 2. Однако не всем модам намагниченной структуры (рис. 4) соответствуют резонансы в спектрах на рис. 2. Например, в TE-спектре при нормальном падении отс утств уют резонансы, соответ-ств ующие точкам A ₂ , B ₂ , C ₂ на дисперсионных кривых (рис. 4), а в TM-спектре отс утств уют резонансы, соответствующие точкам A ₁ , B ₁, C ₁ .

Указанные факты могут быть объяснены из соображений симметрии. Будем называть моду чётной,   если поперечные компоненты полей

E„ = (E , E , H = (H , H \ являются чётными H X' y H функциям по переменной x, то есть

Eh (x) = Eh (-x), Hi (x) = Hi (-x) •(8)

Соответственно, будем называть моду нечётной, если

Ei (x) = -E (-x), H (x) = -H„ (-x).(9)

Рассмотрим сначала ненамагниченную структуру.

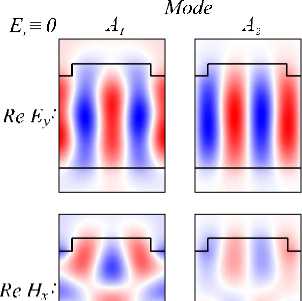
H= 0

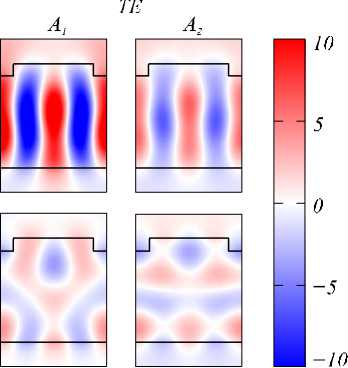
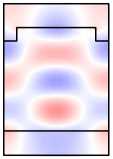
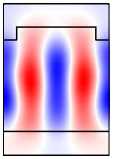
Рис. 5. Ненамагниченная структура: распределение полей мод A ₁ и A ₂ (столбцы 1, 2); распределения поля в структуре, формируемые при падении TE-волн с частотами возбуждения мод A ₁ , A ₂ (столбцы 3, 4)

Рассматрив аемая структура (рис. 1) при отсутствии намагниченности является симметричной, поэтому распределение поля при нормальном падении в ней может быть только симметричным (чётным). Следовательно, при нормальном падении волны в такой структуре можно возбудить только симметричные (чётные) моды с поляризацией, соответствующей поляризации падающей волны. Такими являются мода A ₁ для падающей TE-волны и моды B ₂, C ₂ для падающей TM-волны. Расчётные распределения поля в структуре, формируемы е при падении TE-волн с частотами, соответствующими ТЕ-модам A ₁ и A ₂ , приведены в правой части рис. 5. Рис. 5 показывает, что мода A ₁ действительно возбуждается: распределение поля моды A ₁ (рис. 5, 1-ый столбец) хорошо совпадает с распределением поля в структуре при падающей ТЕ-волне с частотой, соответствующей данной моде (рис. 5, 3-ий столбец). Сравнение 2-го и 4-го столбцов на рис. 5 показывает, что мода A ₂ не возбуждается. Ан алогично, при падении ТМ-волны в структуре также не возбуждаются нечётные моды B ₁ , C ₁ .

Симметрия мод намагниченной структуры

Согласно рис. 2–4, в намагнич енной структуре возб ужд аю тся моды A ₁ , B ₂ , C ₂ , близкие (в смысле

Для простоты обозначим пересечения дисперсионных кривых ненамагниченной структуры (рис. 3) с прямой k_x = 0 точками Ai , B i , C i , i = 1,2 аналогично рис. 4. Для краткости так же будем обозначать и моды, соответствующие этим точкам. На рис. 5 в столбцах 1, 2 приведены расчётные распределения компонент полей ТЕ-мод A ₁ и A ₂ . Рис. 5 показывает, что TE-мода A ₁ является чётной, а TE-мода A ₂ — нечётной. Аналогичный расчёт показывает, что TM-моды B ₁ , C ₁ являются нечётными, а TM-моды B ₂, C ₂ — чётными.

законов дисперсии) к ч ётным модам ненамагни-ченной структуры, а также моды A ₂, B ₁, C ₁ , близкие к нечётным мод ам ненамагниченной структуры и имеющие тип поляризации, отличной от по -ляризации падающей волны. Во зб ужд ению мод A ₁ , B ₂ , C ₂ соотв етствуют магнитооптические эффекты 1-го типа, а во зб ужд ению мод A ₂, B ₁, C ₁ — эффекты 2-го типа.

Для объяснения этих фактов проведем анализ структуры мод в намагниченной структуре.

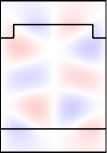
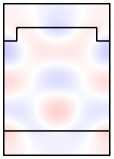
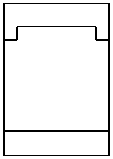
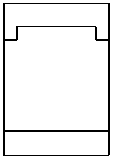
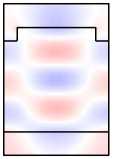
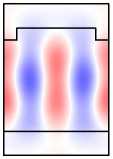
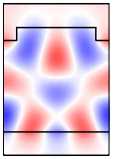
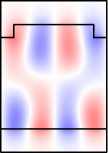
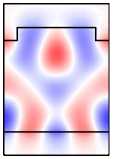
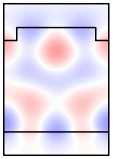
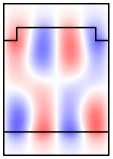
Во-первых, отметим, что в намагниченной структуре каждая из мод Ai,Bi,Ci,i = 1, 2 обладает компонентами обеих поляризаций. Рассмотрим изменение распределений полей мод при намагничивании структуры на примере мод A1 ,A2 (рис. 6, столбцы 1, 2). Сравнивая столбцы 1, 2 на рис. 5, 6, видим, что компоненты поля Ey ,Hx (TE-компоненты), присутствовавшие в модах ненамаг-ниченной структуры, практически не изменились. В то же время в намагниченной структуре у мод появились компоненты Ex , Hy (TМ-компоненты). При этом, если TE-компоненты моды являются чётными, то TM-компоненты будут нечётны ми (мода A1 ). Если TE-компоненты моды являются нечётными, то TM-компоненты будут чётными (мода A2 ). Таким образом, в случае намагниченной структуры некорректно говорить о чётности магнитооптических мод. О чётности можно говорить лишь относительно ТЕ-или ТМ-компонент полей. Можно показать, что в

рассматриваемой намагниченной

Mode

а2

структуре моды

ТЕ

A ₁ , B ₁, C ₁ имеют чётные TE-компоненты и нечётные TM-компоненты. В то же время моды A ₂ , B ₂ , C ₂ имеют чётные TM-компоненты и нечётные TE-компоненты (рис. 6).

а2

тм

ReE,

А,

А?

Re Е

1ml

||||

К)

Re Нх:

О

-5

-10

Re Пу

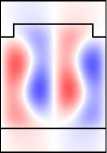
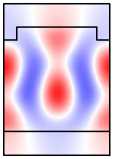
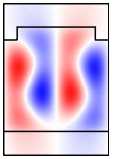
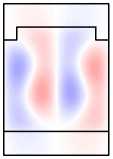
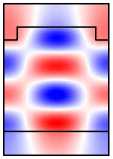
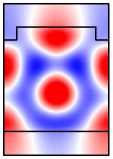
Рис. 6. Намагниченная решётка: распределение поля мод A ₁ и A ₂ (столбцы 1,2);

распределения поля в структуре при возбуждении мод A ₁ , A ₂

и нормально падающей TМ-волной (столбцы 5, 6)

Рассмотрим распределение поля в намагниченной структуре при наличии падающей волны. Из уравнений Максвелла можно получить, что в симметричной периодической структуре с тензором диэлектрической проницаемости (1) компоненты поля удовлетворяют след ующим условиям симметрии. Распределения тех компонент поля, поляризация которых совпадает с поляризацией падающей волны, является чётными, а распределени е компонент противоположной поляризации, которые появляются в намагниченной структуре вследствие конверсии поляризации , являются нечётными. Указанные условия для распределения поля имеют место только при нормальном падении волны. Для иллюстрации указанных условий рассмотрим расчётные распределения полей в структуре, приведенные в столбцах 3–6 на рис . 6.

В столбцах 3, 4 прив едены распределения, формируемые в структуре при падении TE-волн с частотами, соответствующими модам A1 и A2 . Сравне- нормально падающей TЕ-волной (столбцы 3, 4)

ние столбцов (1, 3) и (2, 4) показывает, что мода A ₁ возбуждается в структуре, а мода A ₂ — нет. Действительно, согласно вышесказанному, допустимые распределения поля в структуре при падении ТЕ-волны должны иметь чётные ТЕ-компоненты и нечётные ТМ-компоненты. Этому условию удовлетворяют моды A ₁ , B ₁ , C ₁ . Соответственно при нормальном падении ТЕ-волны моды A ₂ , B ₂ , C ₂ не могут возбудиться.

В столбцах 5, 6 приведены распределения, формируемые в структуре при падении TМ-волн с частотами, соответствующими модам A ₁ и A ₂ . Допустимые распределения поля в структуре при падении ТМ-волны должны иметь чётные ТМ-компоненты и нечётные TE-компоненты. Этому условию удовлетворяют только моды A ₂ , B ₂ , C ₂ . Соответственно из сравнения столбцов (2, 6) и (1, 5) можно видеть, что мода A ₂ возбуждается в структуре, а мода A ₁ — нет.

Таким образом, тот факт, что не всем модам намагниченной структуры соответствуют резонансы в спектрах на рис. 2, объясняется вышеприведенными условиями четности для распределений компонент полей в структуре.

Отметим, что ввиду симметрии структуры при нормаль ном пад ении света ни в нулевом отражённом, ни в нулевом прошедшем порядках дифракции структуры не появляются ко мпо ненты с по -ляризацией отлично й от поляризации падающей волны . В то же время эти компоненты присутствуют в распределении поля в нутри структуры и оказывают значительное влияние на спектр структуры.

При наклонном падении волны на намагниченную структуру формируемое в структуре поле ввиду нарушения симметрии перестает удовлетворять вышеуказанным условиям чётности. На рис. 7 представлены спектры намагниченной и ненамагниченной структур, рассчитанные при различных значениях угла падения. Рис. 7 показывает, что при наклонном падении в спектрах пропускания начинают появляться резонансы, которые отсутствовали при нормальном падении (рис. 2). При этом смещение резонансов точно описывается дисперсионными кривыми на рис. 3, 4.

Отметим, что в общем случае наклонного падения каждому резонансу 1-го типа в TE-спектре соответствует резонанс 2-го типа в TM-спектре и наоборот.

3D

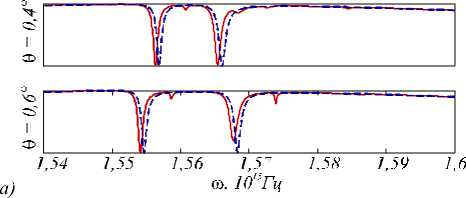
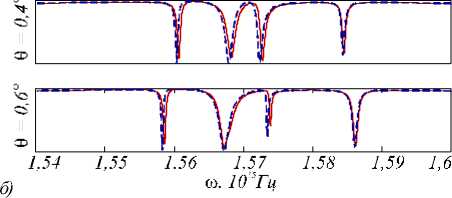
Рис. 7. Спектры пропускания при различных углах падения 6 : для падающих волн с TE-поляризацией (а) и TM-поляризацией (б) (спектры намагниченной структуры — непрерывная линия, ненамагниченной структуры — пунктирная линия)

Заключение

Рассмотрены магнитооптические эффекты, возникающие при дифракции света на намагниченной диэлектрической структуре, состоящей из дифракционной решётки и однородного слоя. Результаты моделирования показывают, что для обоих типов поляризации падающей волны (ТЕ и ТМ) указанная структура обладает магнитооптическими эффектами, состоящими в резонансном изменении пропускания при изменении намагниченности. Изменени е пропускания может достигать 80%.

Рассчитаны дисперсионные кривые мод структуры через вычисление полюсов матрицы рассеяния. Установлено, что спектральные положения магнитооптических резонансов совпадают с условиями возбуждения собственных мод структуры. Показано, что при намагничивании структуры дисперсионные кривые смещаются и дополнительно возникает расщепление дисперсионных кривых.

Магнитооптические резонансы структуры разделены на два типа. Магнитооптические резонансы 1го типа возникают из-за изменения условий возбуждения мод структуры. Изменение условий возбуждения мод описывается смещением дисперсионных кривых, происходящим при намагничивании струк- туры. При нормальном падении волны с ТЕ- (ТМ-) поляризацией резонансы 1-го типа соответствуют возбуждению мод, у которых ТЕ- (ТМ-) компоненты поля близки к чётным модам ненамагниченной структуры с такой же поляризацией. Магнитооптические резонансы 2-го типа происходят при возбуждении мод структуры, имеющих тип поляризаци и «противоположный» поляризации падающей волны. При нормальном падении волны с ТЕ- (ТМ-) поляризацией резонансы 2-го типа соответствуют возбуждению мод, у которых ТМ- (ТЕ-) компоненты поля близки к нечётным модам ненамагниченной структуры с ТМ- (ТЕ-) поляризаци ей.

Использованный в работе метод анализа носит общий характер, что позволяет применять его для исследования магнитооптических мод структур более сложного вида, в частности, анализировать влияние намагниченности на условия возбуждения поверхностных плазмонов либо на резонансы , возбуждаемые в щеля х решётки.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08-014-1), гранта Президента РФ поддержки ве- дущих научных школ (НШ-3086.2008.9) и грантов РФФИ 09-07-12147, 09-07-92421, 07-01-96602.