Исследование математической модели демографических процессов в виде пятифазной системы массового обслуживания

В последние годы в результате экономических и политических изменений в нашей стране возросла потребность в построении научно обоснованных демографических прогнозов. Одним из методов демографического прогнозирования является разработка и исследование математических моделей, в частности применение моделей и методов теории массового обслуживания для моделирования демографических процессов.

В данной статье в качестве математической модели процесса изменения численности женского населения, например женщин Российской Федерации, рассматривается функционирование пятифазной автономной системы массового обслуживания (СМО) с неограниченным числом приборов.

Определим процесс функционирования такой СМО. Будем полагать, что продолжительность обслуживания ф каждой заявки складывается из пяти фаз:

Т = Т 1 + Т 2 + Т 3 + Т 4 + Т 5 .

Здесь все т. - независимые и экспоненциально распределенные случайные величины с параметрами ц , характеризующими продолжительности фаз обслуживания, = 1...5.

Поскольку интенсивность рождаемости существенно зависит от возраста женщин, то целесообразно рассматривать b(t) – интенсивность репродукции как функцию, зависимую от возраста женщины. Для указания такой зависимости рассмотрим систему, в которой три фазы соответствуют различным этапам репродуктивного возраста женщин.

Будем считать, что для заявок, находящихся на обслуживании, на второй, третьей и четвертой фазах возможно генерирование новых требований. Интенсивности генерирования новых заявок равны соответственно b2(t), b3(t) и b4(t). Интенсивности репродукции на первой и пятой фазах будем считать равными нулю, т. е. b1(t) = 0, b5(t) = 0. Поскольку случайные величины т , распределены экспоненциально, то средняя продолжительность -й фазы составляет 1/ц, i = 1...5. Тогда интенсивность репродукции на -й фазе запишем в виде b,( t) = 0,488bi (t )ц, где b (t) – суммарный коэффициент рождаемости в момент t [1]; 0,488 – вероятность рождения девочки;

= 1...5. Обслуживание каждой новой заявки начинается на первой фазе. Заявка, завершив обслуживание на -й фазе, с вероятностью r переходит к обслуживанию на + 1-ю фазу, а с вероятностью 1 – r завершает свое обслуживание и покидает систему, = 1...4. С вероятностью 1 после пятой фазы завершается полное обслуживание заявки.

Поскольку в рассматриваемой системе массового обслуживания отсутствует внешний источник заявок, так как все новые заявки генерируются требованиями, находящимися на обслуживании, а время обслуживания заявок состоит из фаз, то такую систему будем называть автономной системой с фазовым распределением, или PH-распределением времени обслуживания.

В терминах демографии под заявкой подразумевается женщина, репродуктивные вторая, третья и четвертая фазы составляют репродуктивный возраст женщины [1], а время обслуживания в системе - продолжительность ее жизни.

Обозначим через n(t) число заявок, обслуживаемых на i-й фазе в момент времени t. Тогда случайный процесс n (t) = {ni (t), n 2 (t), n 3 (t), n 4 (t), n 5 (t )}T является пятимерной цепью Маркова с непрерывным временем. В терминах демографии ni(t) определяет численность женщин на фазе i, i = 1...5, т. е. в i-й возрастной группе.

Задача исследования данной математической модели состоит в нахождении н аиболее важных числовых характеристик

P ( n i , n 2 , n з , n 4 , n 5 , t ) =

= P { n i ( t ) = n i , n ₂( t ) = n 2 , n з ( t ) = n 3 , n 4 ( t ) = n 4 , n 5 ( t ) = n } , из которых определим первые и вторые моменты.

Для этого распределения запишем систему дифференциальных уравнений Колмогорова [2]: д                „

— { P ( n i , n 2 , n з , n 4 , n 5 , t )} = д t

= - P ( n i , n 2 , n 3 , n 4 , n 5 , t ) { n i P i ■ S n ( b i ( t ) + P i )} + i = 2

+P(ni - 1, n2, n3, n4, n5, t)£ nb (t) + (ni + i)Pi x i=2

x { P ( n + 1, n 2 , n 3 , n 4 , n 5 , t )(i - r ) +

+P(ni +1,n2 -1,n3,n4,n5,t)ri} + (n2 + i)p2 x x{ P (ni, n 2 + 1, n 3, n 4, n 5, t )(1 - Г2) +

+P(ni, n2 +1, n3 -1, n4, n5, t)r2} + (n3 + 1)p3 x x{ P (ni, n 2, n 3 + 1, n 4, n 5, t )(1 - Г3) +

+P(ni, n2, n3 +1, n4 -1, n5, t)r3} + (n4 + 1)p4 x x{ P (ni, n 2, n 3, n 4 + 1, n5, t )(1 - Г4) +

+ P ( n i , n 2 , n 3 , n 4 + 1, n 5 - 1, t ) Г 4 } +

+ ( n 5 + 1) P 5 P ( n , n 2 , n 3 , n 4 , n 5 + 1, t ).

Обозначим характеристическую функцию числа обслуживаемых заявок в пятифазной системе массового обслуживания в момент времени t в виде

H ( u , t ) =

= S P ( ni, n 2, n 3, n 4, n 5, t )eXP{ jSuini}, n1,n2,n 3,n 4,n 5 i = где j = V-1 - мнимая единица; u = {ui, u2, u3, u4, u5}T -пятимерный вектор. Характеристическая функция H(u, t) является функцией векторного аргумента u и скалярного аргумента t.

Умножим (1) на exp{ j' ( u _i n _i + u ₂ n ₂ + u ₃ n ₃ + u ₄ n ₄ + u ₅ n ₅)} и просуммируем по n _i, n ₂, n ₃, n ₄ и n ₅. Получим уравнение для характеристической функции H ( u , t ):

д h ( u , t )_ д h ( u , t )

дt    = j дui Pi x x{1 - e -ju-(1 - r1) - e -ju'eju 2 r} +

+ j S ^ H ^ u^t ) { b ( t )(1 - e^ui) + i = 2     д u i

+P, (1 - e- ju* ) + p, e -^Ju‘ r (1 - e^{J 1}“ + )} + j ^д H ⁽ u , t ) p₅ {1 - e -^{Ju 5} }. (2) д u ₅

Для нахождения числовых характеристик такой системы массового обслуживания применим метод моментов [2].

Известно, что производная k -го порядка в нуле от характеристической функции равна начальному моменту k -го порядка, умноженному на к -ю степень мнимой единицы [3]. Используя этот факт, найдем моменты первого и второго порядков для числа обслуживаемых заявок в рассматриваемой СМО.

Подставим в уравнение (2) его решение и продиффе- ренцируем полученное тождество поочередно по u1, u2, u3, u4, u5. Обозначив дН (u, t)

д u i

u ] = 0, u 2 = 0, u 3 = 0, u 4 = 0, u 5 = 0

= ^jz_i⁽. t ),

i = 1,5,

получим следующую систему пяти обыкновенных дифференциальных уравнений, определяющую компоненты z i ⁽ t ) вектора z ⁽ t ) = ^{ z i⁽ t ), z 2⁽ t ), z 3⁽ t ), z 4⁽ t ), z 5⁽ t ^)} T :

' zi'(t) = -Pi zi (t) + b2 (t)z2 (t) + b3 (t)z3 (t) + b4 (t)z4 (tX z2(t) = P1 ri zi(t) -P2 z2(t),

< z 3⁽ t ) = P 2 ^r 2 z 2⁽ t ) ^-P 3 z 3⁽ t ),                                  ⁽³⁾

z 4⁽ t ) = P 3 r 3 z 3⁽ t ) ^- P 4 z 4⁽ t ),

. Z 5 ( t ) = P 4 Г 4 Z 4 ( t ) -P 5 Z 5 ( t ).

Функция z ( t ) в терминах теории массового обслуживания определяет среднее значение числа заявок, обслуживаемых в системе в момент времени t , а в терминах демографии имеет смысл среднего значения численности женского населения в каждой возрастной группе, определяемой номером фазы.

При b i ( t ) = b i система (3) является линейной системой с постоянными коэффициентами [4]. Особенность этой системы заключается в том, что она распадается на две подсистемы, которые нужно решать последовательно. Аналитическое решение данной системы не представляет затруднения: нахождение собственных значений матрицы коэффициентов приводит к алгебраическому уравнению четвертой степени с комплексно сопряженными корнями. Численное решение выполним ниже при конкретных значениях параметров P _i , r_i и b_i ( t ) = b_i .

Для нахождения моментов второго порядка продифференцируем второй раз поочередно по u _i, u ₂, u ₃, u ₄, u ₅ равенство (2) и, обозначая

^^Н^        =j* di( t), д u*       ui =0, u 2 =0, u 3 =0, u 4 =0, u 5 =0

д ² Н ( u , t )

^{д u}i ^{д u}j u = 0, u ₂ = 0, u ₃ = 0, u 4 = 0, u 5 = 0

j ² d j -( t ),

где d_i ( t ) – второй начальный момент величины n_i ( t ); d_ij ( t ) – второй смешанный начальный момент величин n_i ( t ) и n_j ( t), i = 1...5, j = 1...5, получим систему дифференциальных уравнений:

d 1 ' ( t ) = - 2 ц 1 d 1 ( t ) + 2 ^ d _h. ( t ) b i ( t ) +

= 2

+E bi( t) zi( t)+^ z i( t)’ i=2

d 2 (t) = -2ц2 d 2( t) + 2 d 12( t )ц1 r1 + Ц1 r z1( t) + ц2 z 2( t), d 3' (t) = -2ц3 d 3( t) + 2 d 23( t )ц2 r2 + ц2 r2 z 2( t) + ц3 z 3( t), d 4 (t) = -2ц4 d 4 (t) + 2 d 34 (t )ц3 r3 + ц3 r3 z 3 (t) + ц4 z 4 (t), d 5 (t) = -2ц d 5 (t) + 2 d 45 (t )ц 4 r + Ц4 r z 4 (t) + ц3 z 5 (t), d 1′2 ( t )     (И- + Ц 2) d 12( t)+ d 1( t )И1 ri +

+E d 2i( t ) b( t ) Ц.ri zi( t ), i=2

d 1'3 (t ) = (И + Ц3 ) d 13 (t) + d 12 (t ^2 r2 + E di3 (t ) bi (t), i=2

d u( t ) = - ( ц + Ц 4 ) d 14 ( t ) + d 13 ( t ) ^ 3 r + E d , -4 ( t ) b i ( t ),

= 2

^d 15⁽ t )     ( И . ⁺ И J ^d 15⁽ t ) + ^d 14 ⁽ t ) И 4 ^r 4 + E ^di 5⁽ t ) b i ⁽ t ), (4)

i = 2

d 2 ₃( t ) = - ( и₂ +И₃) d ₂₃( t ) +

+d 13(t)и1 r1 + d22(t)ц2 r2 -ц2r2 z2(t), d 24( t) = -(ц2 +И4) d 24( t) + d 14( t )ц1 r1 + d 23( t )ц3 r3, d25(t)     <“; +И5)d25(t) + d 15 (t)И1 r1 + d24 (t)H4r4, d 34( t)     f“3 + “4> d 34 (t) + d 3( t )И3 r3 + d 24 (t )И2 r2 - И3 r3 z 3( t), d335 (t) = ( И 3 + И )d35 (t) + d34 (t)И4r4 + d25 (t)^2r2 , d 45( t )     <“4 +И5) d45 ( t ) +

^{+ d} 35 ( t )И 3 ^Г3 ^{+ d} 4⁽ t )И 4 r 4 ^- И 4 r 4 z 4⁽ t ),

Очевидно, что d_ij ( t ) = d_ji ( t ), i = 1...5, j = 1...5.

Решение системы (4) нетрудно выполнить при конкретных значениях параметров м _i , r_i и b_i ( t ) = b_i .

Применим предложенную математическую модель в виде автономной системы с PH-распределением времени обслуживания к исследованию демографической ситуации в Российской Федерации.

Предположим, что продолжительность жизни женщины условно можно разделить на пять фаз: средняя продолжительность первой фазы 15 лет, второй фазы – 5 лет, третьей фазы – 10 лет, четвертой фазы – 15 лет и пятой фазы - 30 лет Поскольку продолжительности фаз T i - независимые и экспоненциально распределенные случайные величины с параметрами и , то тогда

_ 1     - 1    - 1     - 1 и = -1

^{И 1} = 15, ^И 2 = 5, ^И 3 10, ^И 3 15, ^И 3 30'

Вторая, третья и четвертая фазы жизни составляют репродуктивный возраст женщины.

Начальной точкой будем считать 2005 г. Исходя из предположений относительно динамики суммарного коэффициента рождаемости, можно сделать прогнозную оценку демографической ситуации. Согласно данным Российского статистического ежегодника [5], суммарный коэффициент рождаемости в 2005 г. составлял 1,287. В последние годы по причине активно проводимой социальной политики ожидается его повышение до значения 2,2. Для построения оптимистического сценария демографической ситуации положим значение суммарного коэффициента рождаемости 2,2 на всем интервале прогнозирования от 2005 до 2105 гг. Тогда, сохраняя пропорциональность коэффициента рождаемости, можно записать b 2( t) = b2 = 0,488 ■ 0,236 -ц2 = 0,023, b3( t) = b3 = 0,488 ■ 1,409 ■Цз = 0,069, b4( t) = b4 = 0,488 ■ 0,568 ■Цд = 0,018.

Будем полагать, что r ₁ = r ₂ = r ₃ = r ₄ = 1. Согласно данным [5], в начальный момент времени t ₂₀₀₅ = 0 имеем следующие начальные условия:

m1(0) = 10,679, m2(0) = 6,017, m3(0) = 11,509, m4(0) = 15,933, m5(0) = 32,733, где mi(t), i = 1...5 – численность женщин соответствующей возрастной группы, млн чел.

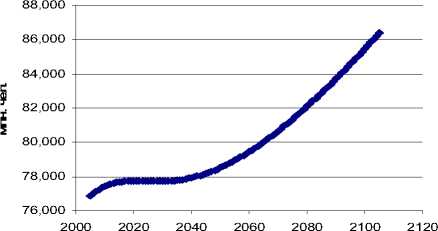
При данных значениях параметров модели система (3) решена в пакете MathCAD, тем самым построен сценарий изменения численности женщин в каждой возрастной группе на долгосрочную перспективу (до 2105 г.) (см. рисунок). Заметим, что, используя решение системы (4), можно найти вторые начальные моменты в долгосрочной перспективе до 2105 г., из которых затем получить значения дисперсий и среднеквадратических отклонений.

годы

Динамика суммарной численности ж енщин

Динамика суммарной численности женщин до 2105 г.

Анализ графика показывает, что при таком предположении о суммарном коэффициенте рождаемости численность женского населения России возрастает. Это означает, что в России необходимо продолжать развитие социальных программ, целью которых является увеличение суммарного коэффициента рождаемости.

Таким образом, предложенная математическая модель демографических процессов в виде пятифазной автономной системы массового обслуживания, а также метод ее исследования могут быть применены для анализа сложившейся демографической ситуации в Российской Федерации и прогнозирования будущих тенденций демографических процессов.