Исследование математической модели управления автоматизированным индивидуальным тепловым пунктом с типовыми регуляторами

автоматизированных ИТП и элеваторных узлов может наблюдаться отрицательный эффект, т.е. отсутствовать экономия тепловой энергии. Этот факт экспериментально был зафиксирован в [7]. В [8] на базе разработанной модели [6] были исследованы с помощью математического моделирования особенности управления автоматизированным ИТП с применением различных типов исполнительных механизмов (ИМ), входящих в состав регулятора системы автоматизации объекта управления (ОУ). При этом было показано, например, что при одних и тех же параметрах контроллера, но с увеличением быстродействия ИМ на базе применения AME 30 (Danfoss) в сравнении с AME 20, возникает режим частого переключения электродвигателя ИМ. В целом это недопустимо, так как приводит к преждевременному выходу из строя электродвигателя ИМ, поэтому это явление должно исключаться путем коррекции параметров контроллера.

Постановка задачи. Исследуются с помощью математического моделирования особенности управления автоматизированным ИТП с известными типовыми регуляторами. За основу математического моделирования исследуемых процессов принят подход [6, 8].

Особенности схем моделирования. Структура типового автоматизированного ИТП для зависимой системы отопления, показанная на рис. 1, содержит технологический контроллер ТК1, моноблок циркуляционных насосов Н1 и Н2 с электроприводами М1 и М2, регулирующий клапан К1 с исполнительным механизмом ИМ1, обратный клапан КО1, регулятор перепада давления прямого действия РД1 с клапаном К2, датчик температуры наружного воздуха ДТ1, датчики температуры теплоносителя ДТ2 и ДТ3, датчики давления ДД1 и ДД2, а также узел учета тепловой энергии, например, теплосчетчик с комплектом датчиков температуры, расхода и давления.

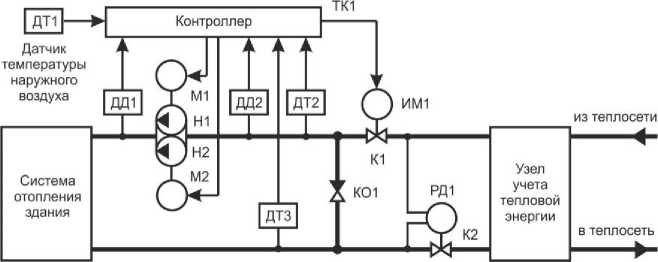
Рис. 1. Блок-схема автоматизированного ИТП здания

Обобщенная функциональная схема системы отопления автоматизированного ИТП здания показана на рис. 2. Состав элементов схемы следующий: блок регулятора по возмущению Р1 (погодная компенсация); двухконтурный блок регулятора Р2 по отклонению технологической величины; П1 – П3 элементы-преобразователи выходных величин датчиков температуры Д1 – Д3 в измеряемые ими физические величины; исполнительный механизм ИМ; регулирующий орган РО в виде седельного клапана; узел смешивания теплоносителей УС (см. рис. 1) от присоединяемых тепловых сетей и от обратного трубопровода системы отопления здания через перемычку с обратным клапаном; объект управления ОУ, представляющий собой СО здания.

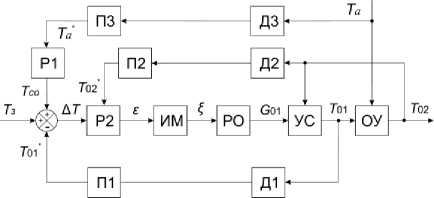
Рис. 2. Функциональная схема автоматизированного ИТП здания

Обозначения основных величин функциональной схемы следующие: Та – исходная температура наружного воздуха; Та* – температура наружного воздуха на входе в блок Р1; Тсо – требуемая в соответствии с принципом погодной компенсации расчетная температура теплоносителя в подающем трубопроводе СО здания после перемычки с обратным клапаном (см. рис. 1); Тз – расчетное отклонение температуры теплоносителя в подающем трубопроводе СО здания, заданное диспетчером с целью коррекции Тсо; ΔТ – отклонение по температуре регулируемой величины T01; ε – приведенный управляющий сигнал регулятора Р2; ξ – приведенная величина перемещения РО; G01 – расход теплоносителя после РО, т.е. перед перемычкой с обратным клапаном; Т01 – температура теплоносителя в подающем трубопроводе внутреннего контура СО здания; Т01 – измеренная температура теплоносителя в СО здания; Т02 – температура теплоносителя в обратном трубопроводе СО здания; Т02* – измеренная температура теплоносителя на входе в Р2.

Система уравнений математического моделирования. Математическая модель СО здания на основе автоматизированного ИТП в соответствии с функциональной схемой и с учётом структур регуляторов Р1 и Р2 (в целях упрощения схемы на рис. 2 их структуры не раскрыты) представлена в виде системы уравнений (1).

dT a *( t )       *

T da     7     + Ta (t)   kdaTa (t), dt

*

t- 1           + T01* ( t) = kd 1T01( t), dt

T o ( t ) = f , ( T a ),

AT(t) = Tc0 (t) + T3 (t) - Toi (t), x i(A T) =

0, - X - T ( t ) <  X - , k i A T ( t ), |A T ( t )| >  X - ,

8( t) - ^ [x 1(A T) Tu+^x^ATI, fk2f(t), - km < 8(t) < km ,

X-) ( t ) = 5        ,       ,

[ k m , ^{8 (} t )| >  k m ,

• ^-( ⁽ t ⁾ = k u x 2 ( t ),

• ^{-t      T} u

G 01 ( t ) = G 1 k_ke^{k 2} ^ ⁽ t ) ,

T 1 G 01 (t) + T 02 (t)(G co - G 01 0^)) = G co T 01 (t) ,

T 1 T 2 ^d^T °2^ ^{t )} + ( T 1 + T 2 ) ^dT ⁰2^ ^{t )} + T 02 ( t ) = kT 01 ( t ), dt                 dt

*

• ^{dT 02 (} t )   _T *

Td 2            + T02 (t )   kd 2 T 02( t ), dt

Система (1) включает следующие уравнения: уравнения движения датчиков температуры Д3 и Д1; уравнения для регуляторов Р1 и Р2 (уравнение отопительного графика для вычисления расчетной температуры теплоносителя в подающем трубопроводе СО здания Т со ; уравнение связи для определения Δ Т ; нелинейное уравнение зоны нечувствительности регулятора; уравнение регулятора Р2 для управления в системах теплоснабжения, например, по аналогии со специализированными контроллерами типа ECL Comfort; нелинейное уравнение зоны ограничения);

уравнение исполнительного механизма (считается интегрирующим звеном); уравнение РО относительно выходной величины G ₀₁; уравнение связи для УС; уравнение движения ОУ по каналу регулирования «температура теплоносителя Т ₀₂ -температура теплоносителя Т 01 »; уравнение движения датчика температуры Д2.

Дополнительные обозначения в системе уравнений (1) следующие: τ di и k di – соответственно постоянная времени и коэффициент передачи i -го датчика температуры; G co – расход теплоносителя во внутреннем контуре СО здания, определяемый циркуляционным насосом (см. рис. 1); G ₁ – номинальный расход теплоносителя на входе РО; Т 1 – температура теплоносителя в подающем трубопроводе на вводе в ИТП; x ₁(Δ Т ) – выходная величина нелинейной зоны нечувствительности регулятора Р2; x 2 ( t ) – выходная величина нелинейной зоны ограничения (насыщения) в регуляторе Р2; k 1 и k 2 – коэффициенты пропорциональности соответственно нелинейных зон нечувствительности и ограничения регулятора Р2; X_d – зона нечувствительности регулятора Р2; X p – зона пропорциональности регулятора Р2; Т и – постоянная регулятора Р2.

Основные результаты расчётов. На основе математической модели СО здания (см. систему уравнений (1)) с помощью имитационного моделирования в среде Simulink исследуем законы регулирования 2-х типов: пропорционально-интегрального и интегрального, формируемые блоком регулирования Р2 контроллера с применением определённого типа исполнительного механизма. Уравнение для определения величины тепловой мощности W ( t ) в здании с учётом применения автоматизированного ИТП следующее:

W ( t ) = G ₀₁( t)T*_X(.t ) - G ₀₂( t)T_to(tt ) . (2)

Параметры моделирования. Считаем, что в начальный момент времени t =0 выполняется переход автоматизированного ИТП здания в режим пониженного теплопотребления за счет уменьшения T_з на 5°C. В итоге температура теплоносителя T со также уменьшается на 5°C. Исходные параметры для имитационного моделирования в среде Simulink представлены в табл. 1.

Таблица 1. Исходные параметры для моделирования

Наименование параметра, его обозначение	Величина, размерность
коэффициент  преобразования  объекта управления, k	0,807
постоянная времени объекта управления, τ 1	1337 с
постоянная времени объекта управления, τ 2	759 с
начальная температура теплоносителя в системе, T 2	48,2°C
максимальный расход на вводе в ИТП, G 1	14,7 м 3 /ч
максимальный расход в СО здания, G со	16 м 3 /ч
температура наружного воздуха, T a	-1,0°C
начальное положение штока клапана ИМ	74,6%
параметр регулятора Р2, k m	100%
параметр регулятора Р2, X d	0°C

Учитывая, что исследуются контроллеры типа ECL Comfort (Danfoss), поэтому и остальные элементы автоматизации объекта управления (ОУ) принимаем этой же фирмы. Основные характеристики датчиков времени представлены в табл. 2.

Таблица 2. Постоянные времени датчиков температуры

Тип датчика	Назначение и условное обозначение	Величина, размерность
ESMU-100	Погружной медный датчик температуры теплоносителя в гильзе, τd 1	32 с
ESMT	Датчик температуры наружного воздуха, τ da	900 с

Основные характеристики регулирующего клапана РО типа VB2 фирмы Danfoss, представлены в табл. 3.

Таблица 3. Характеристики регулирующего клапана типа VB2

Наименование параметра, его обозначение	Величина, размерность
диаметр, D у	40 мм
коэффициент, k kvs	25 м3/ч
условное давление, Ру	2,5 МПа
температура, Т min	5 °C
температура, Т max	150 °C
ход штока, h	10 мм

Технические характеристики исполнительного механизма типа AME 20 фирмы Danfoss для работы с регулирующим клапаном VB2 представлены в табл. 4.

Таблица 4. Характеристики исполнительного механизма AME 20

Наименование параметра	Величина, размерность
напряжение	24 В
частота	50/60 Гц
потребляемая мощность	4 Вт
тип управляющего сигнала	аналоговый
развиваемое усилие	450 Н
ход штока	10 мм
время перемещения штока на 1 мм	15 с/мм
входной сигнал 1	0 – 10 В; R i = 24 кОм
входной сигнал 2	0–20 мА; R i =500 кОм
выходной сигнал	0(2) – 10 В
наличие возвратной пружины	нет
минимальная температура окружающей среды	0 °C
максимальная температура окружающей среды	55 °C

Результаты моделирования. Регулятор автоматизированной системы для ОУ [9] включает контроллер с блоком регулирования Р2 и исполнительный механизм ИМ (см. рис. 2), их уравнения движения представлены в системе уравнений (1). В отличие от [8] в этой работе на основе применения ИМ типа AME 20 (см. табл. 2) изменяются параметры блока регулирования контроллера и вид закона, который он формирует с учётом исследуемого типа регулятора. Длительность моделирования при исследованиях во всех случаях 1 час 45 мин.

Вариант 1. Исследуется пропорциональноинтегральный закон регулирования (ПИ-регулятор), формируемый блоком регулирования Р2 контроллера с применением ИМ типа AME 20. Уравнение движения блока регулирования Р2, имеет вид (см. систему уравнений (1)):

^ ( t ) = km- x , ( A TT + p -

dx. ( A T ) dt

где X p 80°C, T u =10 с. Исходное уравнение (3) в ПИ-регуляторе затем интегрируется ИМ. Это важная особенность рассматриваемого контроллера. Результаты имитационного моделирования с учётом данных X p , и T u по этому варианту исследований показаны на рис. 3.

Анализ исследуемых динамических характеристик в виде изменений температуры теплоносителя T ₀₁ на вводе в СО здания в увеличенном масштабе времени (см. рис. 3а) и температуры теплоносителя T 02 в обратном трубопроводе на выходе из СО здания (см. рис. 3б) показывает, что они имеют вид апериодических переходных процессов. В этом случае расчетное теплопо-требление здания составляет величину порядка 1,08502 ГДж. Увеличим в уравнении (2) время, т.е. принимаем его как T_u =60 с. Результаты имитационного моделирования показаны на рис. 4.

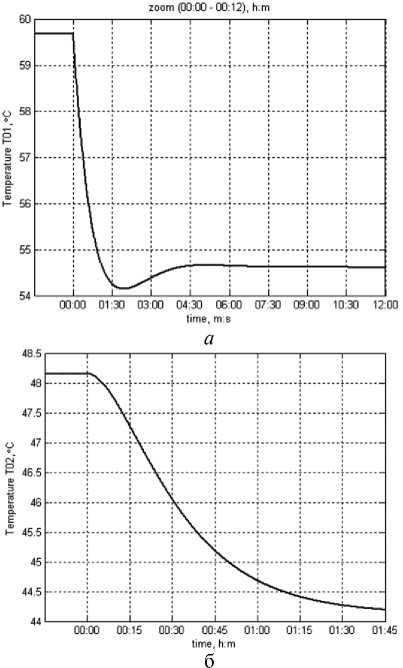
Рис. 3. Зависимости изменений T 01 на вводе в СО здания ( а ) и T 02 в обратном трубопроводе на выходе из СО здания ( б )

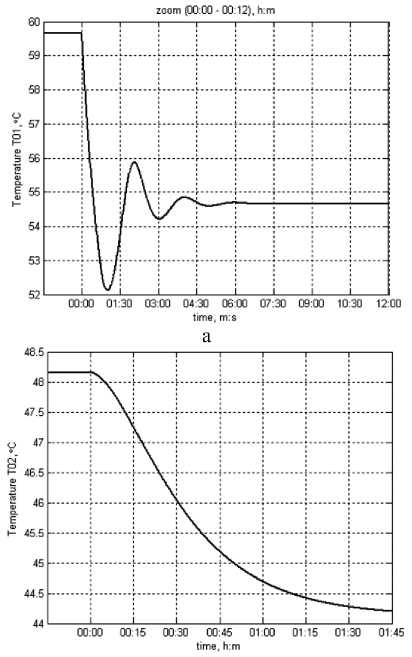
б

Рис. 4. Зависимости изменений T ₀₁ ( а ) и T ₀₂ ( б ) СО здания

Анализ исследуемых динамических характеристик в виде изменений T ₀₁ на вводе в СО здания в увеличенном масштабе времени (см. рис. 4а) и температуры теплоносителя T 02 в обратном трубопроводе на выходе из СО здания (см. рис. 4б) показывает, что наблюдается для T 01 переходный процесс колебательного вида. Расчетное теплопотребление порядка 1,08858 ГДж.

Вариант 2. Исследуется интегральный закон регулирования (И-регулятор), формируемый блоком регулирования Р2 контроллера с применением аналогичного ИМ. В связи с этим уравнение движения блока регулирования Р2 заменяется в системе уравнений (1) на уравнение вида:

=( t) = km- [*1(A T )T ],          (4)

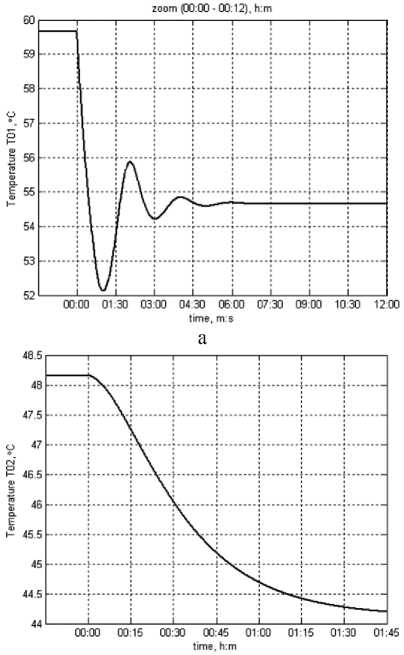
X где Xp=80°C, Tu=60 с. Исходное уравнение (4) в И-регуляторе затем интегрируется ИМ. Результаты имитационного моделирования для этого варианта показаны на рис. 5.

б

Рис. 5. Зависимости изменений T ₀₁ ( а ) и T ₀₂ ( б ) СО здания

Анализ исследуемых динамических характеристик в виде изменений температуры теплоносителя T01 на вводе в СО здания в увеличенном масштабе времени (см. рис. 5а) и температуры теплоносителя T02 в обратном трубопроводе на выходе из СО здания (см. рис. 5б) показывает, что наблюдается для T01 переходный процесс колебательного вида. Расчетное теплопотребление здания в исследуемом случае порядка 1,08535 ГДж.

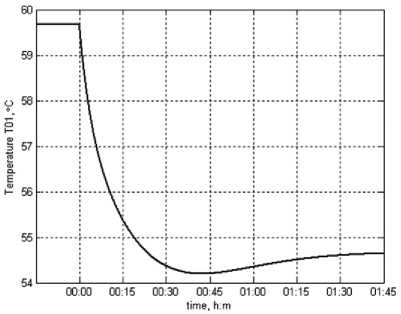
В уравнении (3) принимаем следующие значения параметров: X p =100°C, T u =1 с. При проведении всех исследований выбирались значения T u =const с учётом того, что T u больше или меньше времени перемещения штока клапана с помощью ИМ (см. табл. 4). Результаты имитационного моделирования с учётом выбранных значений X p и T u показаны на рис. 6.

а

б

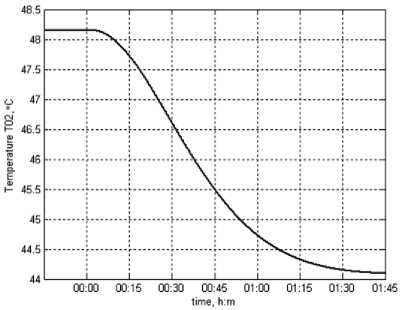
Рис. 6. Зависимости изменений T ₀₁ ( а ) и T ₀₂ ( б ) СО здания

Анализ исследуемых динамических характеристик в виде изменений T 01 на вводе в СО здания в увеличенном масштабе времени (см. рис. 6а) и температуры теплоносителя T 02 в обратном трубопроводе на выходе из СО здания (см. рис. 6б) показывает, что они имеют вид апериодических переходных процессов. Как и следовало ожидать, расчетное теплопотребление здания уменьшилось до величины 1,08456 ГДж.

Сравнительный анализ полученных результатов для исследуемых 2-х законов регулирования, формируемых блоком регулирования Р2 контроллера с применения ИМ типа AME 20 при различных параметрах блока контроллера, показал следующее:

• 1)    для ПИ-регулятора расчетное теплопотребле-ние здания незначительно увеличивается с 1,08502 ГДж до 1,08858 ГДж при возникновении колебательного переходного процесса;

• 2)    для И-регулятора расчетное теплопотребление здания находится на уровне аналогичном как для ПИ-регулятора и незначительно увеличивается

  при колебательном переходном процессе с 1,08456 ГДж до 1,08535 ГДж.

Переходные процессы колебательного вида для ИМ должны быть исключены, так как они приводят к преждевременному выходу из строя электродвигателя ИМ. Для устранения колебательных процессов, появившихся в автоматической системе регулирования автоматизированного ИТП при исследуемых процессах, необходимо изменить настроечные параметры регулятора с учётом заданного времени перемещения штока с помощью ИМ.

Выводы:

• 1.    Представлены возможности математического моделирования управления автоматизированным ИТП здания с известными типовыми регуляторами. С помощью имитационного моделирования в среде Simulink исследованы и выявлены особенности автоматизированного ИТП на базе применения ПИ- и И-регуляторов.

• 2.    В инновационных технологиях, внедряемых при создании автоматизированных ИТП зданий, необходимо учитывать полученные результаты, которые показали, что теплопотребле-ние здания при типовых законах регулирования находится приблизительно на одном и том же уровне и поэтому для регулирования процесса отопления здания имеется возможность практического применения И-регулятора, так как он проще в реализации и в настройке.

• 3.    Анализ переходного процесса с учётом температуры теплоносителя T 02 в обратном трубопроводе здания показывает, что ОУ является низкочастотным фильтром по отношению к существенным колебаниям на его вводе (в подающем трубопроводе).

• 4.    В отличие от известных методик определения параметров блока регулирования контроллера на основе расчётной переходной характеристики последовательного соединения ОУ и датчика температуры с помощью разработанной математической модели имеется возможность

определять не только оптимальные параметры настройки блока регулирования, но прежде всего параметры теплоносителя при возможных изменениях как в структуре элементов автоматизированного ИТП, так и в СО здания или сооружения.