Исследование матричного метода вычисления вытянутых сфероидальных функций нулевого порядка

Вытянутые сфероидальные функции (ВСФ) нулевого порядка Vn(c,x) являются собственными функциями интегрального уравнения с sinc-ядром [1-4] и преобразования Фурье [5], что позволяет эффективно использовать их во многих областях науки и техники: теория синтеза антенн, восстановление объектов по изображению, сверхразрешение, теория резонаторов [1-10].

Подходы к вычислению ВСФ произвольного порядка отличаются сложностью и трудоемкостью: представление через ряды по другим, более простым базисам [11-13], решение дифференциального уравнения методом ортогональной дифференциальной прогонки с переносом граничных условий из особых точек [14]. Для расчета ВСФ нулевого порядка можно дополнительно воспользоваться присущими только им свойствами и решать интегральное уравнения на собственные значения, например, итерационно [15].

Учитывая трудоемкость упомянутых подходов, в одном случае [16,17] и чувствительность к начальному приближению, в другом [15], желательно иметь простой и устойчивый метод расчета ВСФ нулевого порядка. В работах [8,10] предлагается вместо интегрального уравнения на собственные значения решать матричное уравнение, полученное путем дискретизации.

В данной работе проводится исследование матричного метода вычисления ВСФ нулевого порядка, реализованного с исполь зованием программного обеспечения Matlab. Работоспособность оценивается по выполнению основных свойств рассчитанных функций: ортогональность, инвариантность к интегральному преобразованию с sinc-ядром и преобразованию Фурье. Правильность упорядочивания функций определяется по убыванию собственных значений. Целью работы является определение границ работоспособности метода.

Основные свойства ВСФ нулевого порядка

ВСФ произвольного порядка являются решением скалярного волнового уравнения в вытянутых сфероидальных координатах. После разделения переменных трехмерного волнового уравнения в этих координатах возникает дифференциальное уравнение [18]:

d « тХ^(x) I 2 2 m2 1 / ч n m — (1 -x2V4-1 + 1 X — c2x2-" г Иx) = 0, (1) dx           dx I            1 - x I которое имеет непрерывное вещественное решение y(x), ограниченное при любых х. С точностью до константы решение единственно. Здесь и далее, c - произвольное положительное число, m - неотрицательное целое.

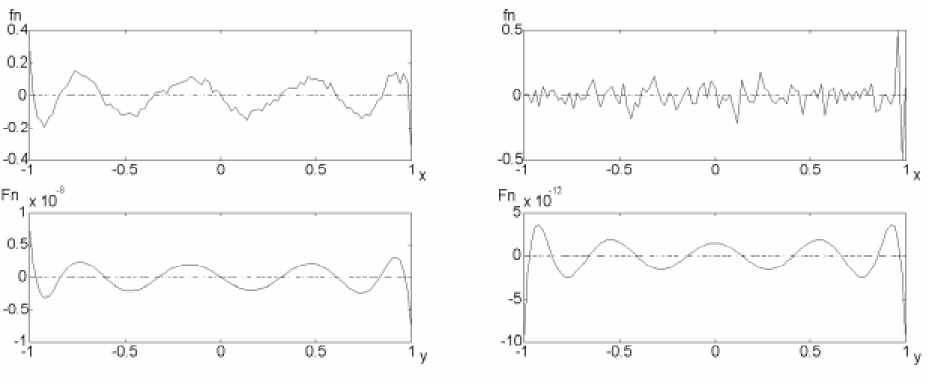
Обозначим специальные значения %, при которых существуют непрерывные решения через Хтп, п = m, m+1... . Эти собственные значения могут быть так обозначены, поскольку 0

Функции Vmn(x) известны [11-13] как, вытянутые сфероидальные волновые функции порядка т. Однако особый интерес представляют ВСФ нулевого порядка. Благодаря ряду замечательных свойств [1-5] они играют важную роль во многих прикладных задачах [1-10].

Функции V_0n(x), которые далее будем обозначать просто V_n(x) удовлетворяют интегральному уравнению [18]:

,          1 sin (y - x)]

^AnVn y ) = J ——Vn x) d x, (2)

-i n y - x )

где X_n - собственные числа:

1 > X₀ > Х1 > ... > 0 .           (3)

При этом собственные числа интегрального преобразования определяют количество энергии соответствующей собственной функции, концентрирующейся на данном ограниченном интервале. Собственные числа близкие к единице показывают, что данная ВСВФ имеет за пределами данного интервала малую долю энергии. Если рассматривать Х_п как функцию от n, то собственные числа имеют характерную особенность поведения: до некоторого п_о 2с п они имеют значения близкие к единице, а после - резко спадают до нуля.

ВСФ нулевого порядка являются также собственными функциями преобразования Фурье на ограниченном интервале [5,7,18]:

a_nV_n У)= jexpicxV_n (x)dx , -1

^A =         •               (⁴⁾

В [1] предложено следующее правило нормировки:

T/2

jVn x^Vm ^X)dX= ^§mn ^n,

-T /2 +^ j V n x)V m x^)dx= § mn . -^

Также ВСФ нулевого порядка являются собственными функциями для sinc-преобразования (2) и преобразования Фурье (4) на

бесконечном интервале [5, 7, 18].

Исследование матричного метода

Рассмотрим модифицированное интегральное уравнение (2):

T/2

kVn У)= j Vn x)

-T /2

■ 2c

Si n— У - x)

—LT-------J dx, (6)

п У - x)

где параметр с = nWT, T- ширина интервала в объектной области, W - ширина интервала в частотной области.

Пусть N - число точек дискретизации, тогда получим дискретный вариант уравнения (6)

N -1

lnyn= Zyn xi)

l=0

■ 2c .              .

^Sin— yk ^-xi) T

^p(Ук ^-xi)

k = 0,N ,              (7)

который можно записать в матричном виде:

^AnVn = ^SVn .          ⁽⁸⁾

Решать уравнение (8) можно с помощью прикладных пакетов программ, например, Matlab. Заметим, что матрица S квадратная, и число точек дискретизации N определяет также общее количество вычисляемых функций.

Проверка свойства ортогональности.

Для проверка свойства ортогональности функций, рассчитанных матричным методом (7)- (8) вычислялись следующие величины:

N -1

Е V AVm xk)

A_nm=       ;------------, n,m = 0,M .(9)

nm          N -1                                         V /

Е vnxk) k = 0

Критерием выполнения свойства ортогональности (5) может служить величина:

MM

D = 2ЦА nml+EH-Anml, (10) n=0m ^n            n=0

которая в идеале д.б. равна нулю. В таблице 1 приведены значения величины D для десяти первых функций (в ур. (10) M=9) с различным параметром с.

Таблица 1. Выполнение свойства ортогональности для M = 9, N = 101

	с=2	c=5	c=10	c=20
D	1,0463 -IQ-14	1,4003-10-14	9,6979-10-15	1,9848-10-14

Из таблицы 1 можно сделать вывод о выполнении свойства ортогональности для полученных собственных функций.

Проверка выполнения свойства инвариантности к преобразованию с sinc-ядром.

Выполнение этого свойства оценивалось по среднеквадратичному отклонению "выходной" i/_n (у ) функции после преобразования (7) от "входной" ^_n(x):

5 _^ N -1 Sk k=0 Xk )- V n Xk >1 N -1 S V n2Xk)       ’ k=0 (11) где функции ^Пп (у), Vn(x) предварительно выровнены по максимуму.

Результаты для некоторых значений параметра c=10, 20 приведены в таблице 2 и 3, соответственно. Значения Xn в таблицах 2 и 3 вычислялись исходя из ур. (2) как отношение максимумов функций i/n (у) и Vn(x) на одинаковых интервалах, то есть max {^/n (у)} л _ [-T /2T /2]

ⁿmax {// X)}.        ⁽¹²⁾

[-T /2,T /2] ⁿ

Из таблиц 2, 3 видно, что не выполняется свойство о не возрастании собственных чисел Xn. Ранжировка полученных функций была проведена в соответствии с (3), что скорректировало порядок, установленный встроенной функцией Matlab.

Из таблиц 2 и 3 также видно, что свойство (2) нарушается, начиная с некоторого номера n_c, зависящего от параметра с, при чем n_c > n₀. Так, например,

• -    для с=2: n₀=1, n_c=8,

• -    для c=5: n₀=3, n_c=11,

Таблица 2. Значения %_пи ошибки 8 (11) для с=10, N=101, M=18

Номер функции (Matlab)	Скорректированный номер функции	Значение ln	Ошибка, d
6	0	0,99999	1,1781-10-15
5	1	0,99998	7,7543-10-16
4	2	0,99993	7,2443-10-16
3	3	0,9982	6,5013-10-16
2	4	0,9778	7,3094-10-16
0	5	0,8419	7,0206-10-16
1	6	0,4678	1,0162-10-15
7	7	0,1254	2,7448-10-15
8	8	0,0173	1,0685-10-14
9	9	0,0016	7,1481-10-14
10	10	0,0001	1,2566-10-12
11	11	5,7821-10-6	1,8201-10-11
12	12	2,6109-10-7	4,2788-10-10
13	13	9,9312-10-9	1,5854-10-8
14	14	3,2293-10-10	3,7692-10-7
15	15	9,0837-10-12	1,6731-10-5
16	16	2,2325-10-13	4,3169-10-4
17	17	4,8268-10-15	0,0204
18	18	1,5834-10-16	2,6302

Таблица 3. Значения Х_пи ошибки 8 (11) для с = 20, N = 101, M = 27

Номер функции (Matlab)	Скорректированный номер функции	Значение ln	Ошибка, d
16	0	0,999999	9,7149-10-15
15	1	0,999998	8,6180-10-16
14	2	0,999996	1,4720-10-15
13	3	0,999992	1,0531-10-15
12	4	0,99999	1,2603-10-15
11	5	0,99997	8,5340-10-16
9	6	0,99993	1,2798-10-15
8	7	0,9999	8,0873-10-16
6	8	0,9998	5,4342-10-16
5	9	0,9981	1,0142-10-15
3	10	0,9840	2,2465-10-15
1	11	0,9019	1,3170-10-15
0	12	0,6365	2,2044-10-15
4	13	0,0621	1,1603-10-14
2	14	0,2667	2,6452-10-15
7	15	0,0095	2,7672-10-14
10	16	0,0011	2,3090-10-13
17	17	1,0868-10-4	1,7534-10-12
18	18	9,1571-10-6	2,9481-10-11
19	19	6,7550-10-7	4,1404-10-10
20	20	4,4129-10-8	5,2743-10—9
21	21	2,5752-10-9	1,0669-10-7
22	22	1,3519-10-10	1,7211-10-6
23	23	6,4209-10-12	3,0271-10-5
24	24	2,7739-10-13	8,1059-10-4
25	25	1,0941-10—14	0,0195
26	26	4,9774-10-16	0,4351
27	27	3,9142-10-16	0,9099

• -    для c=10: n₀=6, n=16,

• -    для c=20: n₀=12, nc=24.

Индексы nc, n₀ определяют границы применимости метода:

• -    для n< n₀ значения X_n = 1, и величина ошибки 8 <<1% и имеет значение отличное от нуля в четырнадцатом порядке;

• -    для n₀< n< п_с значение ошибки 8 приемлемо и порядок ее не более 1%, причем числа X_n имеют значения отличные от нуля в порядке меньше или равном пятнадцати;

• -    для n > nc величина ошибки 8 становится не приемлемой, а числа X_n имеют значения отличные от нуля в порядке больше или равном шестнадцати;

Следует отметить, что в прикладных задачах наибольший интерес представляют случаи, когда Xn = 1, когда рассматриваемый метод демонстрирует хорошие результаты.

Проверка выполнения свойства инвариантности к преобразованию Фурье.

Выполнение этого свойства оценивалось по среднеквадратичному отклонению "выходной" i/_n (у ) функции после преобразования (4) от "входной" V_n(x).

На рис.1,2 приведены графики абсолютных значений собственных функций V_B(x) и их Фурье-образов i^_n (у) для различных параметров. Из рисунков 1 и 2 видно, что при

Рис. 1. Графики абсолютных значений собственных функций / (x) (abs(fn)) и их Фуръе-образов / _n (у ) (abs(Fn)) для N=101, c=2, n=0 (а), n=1 (б), n=3 (в)

Рис. 2. Графики абсолютных значений собственных функций /_n(x) (abs(fn)) и их Фуръе-образов ц/ у) (abs(Fn)) для N=101, c=10, n=6 (а), n=1 (б), n=8 (в)

значениях Xn = 1 энергия ВСФ сконцентрирована на интервале [-T /2, T /2], и, наоборот, при значениях Xn = 0 вне этого интервала. Однако, вид функции внутри интервала после преобразования Фурье не меняется с точностью до множителя.

Из таблицы 4 видно, что ошибка 8 становится не приемлемой только, если собственные значения Xn намного меньше единицы, при значениях Xn близких к единице значение ошибки стремится к нулю.

Недостатки метода

Выше было показано, что полученные собственные функции удовлетворяют основ ным свойствам ВСФ при Xn = 1.

Однако, из таблиц 2-4 видно несоответствие номеров собственных функций порядку собственных чисел. Правильно отранжи-ровать ВСФ можно, используя (12) и (3).

При уменьшении Xn наблюдается не только нарушение свойств ВСФ, но и искажение вида функций. Например, собственные функции на рис.3. Нужно при этом отметить фильтрующее свойство преобразования Фурье - после его применения функции приняли стандартный вид. Преобразование с sinc-ядром такого эффекта не дало. Однако "выглаживание" рассчитанных функций с помощью (4) снижает ошибку в выполнении

Таблица 4. Значения отклонения абсолютного значения ВСФ и их Фурье-образа для M = 9, N = 101

Номер функции (Matlab)	с=2		с=10
	Собственные числа, ln	Ошибка, d	Собственные числа, ln	Ошибка, d
0	0,8929	0,0046	0,8394	0,0419
1	0,3678	0,0047	0,4719	0,0537
2	0,0395	0,0169	0,9796	0,0374
3	0,0014	0,0439	0,9984	0,0307
4	0,0000	0,0804	0,9988	0,0228
5	0,0000	0,1244	0,9996	0,0154
6	0,0000	0,1743	0,9999	0,0099
7	0,0000	0,2286	0,1422	0,0728
8	0,0000	0,2840	0,0225	0,1253
9	0,0000	0,2805	0,0024	0,1866

• (2)    только при X_n = 1, в остальных случаях ошибка даже увеличивается.

Заключение

В данной работе реализован и исследован матричный метод вычисления ВСФ нулевого порядка с использованием программного обеспечения Matlab. Исследование метода заключается в проверке получаемых функций на выполнение основных свойств. Результатом данной проверки являются следующие выводы:

• 1.    Данный метод позволяет получать удовлетворительную точность только в некотором диапазоне изменения индекса п, обеспечивающие X_n = 1. Верхней границей диапазона можно считать п₀ = 2с/п.

• 2.    Выполнение свойства инвариантности к интегральному преобразованию с sinc-ядром обеспечивается с более высокой точностью, чем свойство инвариантности к преобразованию Фурье. В первом случае отклонение составляет менее 1% даже для функций с X_n = 10^-13. Во втором случае отклонение было меньше 5% только для п<п₀.

• 3.    Недостатком метода также является неправильное упорядочивание вычисляемых функций, которую нужно корректировать в соответствии с убыванием X_n.

• 4.    При X_n = 0 наблюдается не только нарушение свойств ВСФ, но и искажение вида функций. "Выгладить" такие функции можно с помощью преобразования Фурье, однако ошибка при этом снижается только при X_n=1.

  

  а)                                                     б)

  Рас. 3. Графики абсолютных значений собственных функций у_п(х) (fn) и их Фурье-образов у_n (y) (Fn) для N = 101, c = 2, п = 9 (а), п = 10 (б)

  
  

Тем не менее, учитывая простоту реализации, рассмотренный метод может успешно применяться в практических задачах, использующих ВСФ с собственными чисел близкими к единице.

Работа поддержана Российским фондом фундаментальных исследований (гранты 0015-96114, 00-01-00031).